2022全国数学建模-C 题复盘 古代玻璃制品的成分分析与鉴别

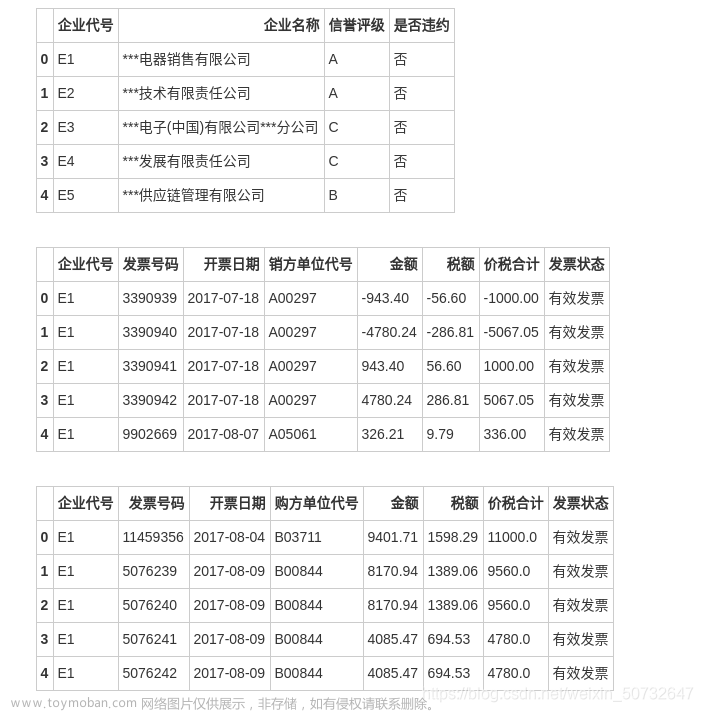
上个月参加了全国数学建模大赛做了C题，很幸运获得省一并送评国奖，整理了一下程序并重新复盘了一下，在这里简单展示问题一、二、三的部分小问解题思路与过程以及python程序。

读取、展示数据：

# 读取数据
data1 = pd.read_excel('附件.xlsx',sheet_name='表单1')
data2 = pd.read_excel('附件.xlsx',sheet_name='表单2')
data3 = pd.read_excel('附件.xlsx',sheet_name='表单3')

data1: 

 data2:

data3:

预处理：

1）填补表单1颜色缺失值以及表单2化学成分缺失值

对除颜色外的三个特征：类型、纹饰、表面风化进行分组，提取颜色的众数来对特定样本点进行填充缺失颜色。

def get_yanse(x):
    return x.value_counts().index[0]
display(data1.groupby(['类型','表面风化','纹饰'])['颜色'].agg(get_yanse,))
"""
类型  表面风化  纹饰
铅钡  无风化   A     浅蓝
          C      紫
    风化    A     浅蓝
          C     浅蓝
高钾  无风化   A     蓝绿
          C     浅蓝
    风化    B     蓝绿
Name: 颜色, dtype: object
"""

data1[data1['颜色'].isna()]
""""""
文物编号	纹饰	类型	颜色	表面风化
18	19	A	铅钡	NaN	风化
39	40	C	铅钡	NaN	风化
47	48	A	铅钡	NaN	风化
57	58	C	铅钡	NaN	风化
""""""

# 发现缺失数据的对应众数颜色均为浅蓝，使用浅蓝进行填充
data1.fillna('浅蓝',inplace=True)

 依据题意对表单2化学成分缺失值进行0填充

data2.fillna(0,inplace=True)

2）提取出表单2数据文物采样点特征中的文物编号信息，通过文物编号信息联结表单1 

# 提取文物采样点中的文物编号信息
def get_number(x):
    number = re.findall('\d*',x)[0]
    number = int(number[1]) if number[0]=='0' else int(number)
    return number
data2['文物编号'] = data2['文物采样点'].apply(get_number)

# 通过文物编号关联表单1、表单2
data_merge = pd.merge(data1,data2,on = '文物编号')

3）去除化学成分和在85%~105%外的无效数据

查看无效数据：

data_merge[~((zong_chengfen >= 85) & (zong_chengfen <= 105))]

# 取出有效数据
data_merge = data_merge[(zong_chengfen >= 85) & (zong_chengfen <= 105)]
# data_merge.to_excel('问题一连接两表并处理后数据.xlsx')

 4）对联结后的数据依据题目附件信息描述以及文物编号、文物采样点信息，获取采样点的风化类型。

# 获取采样点风化类型信息
# 第一步
def get_fh(x):
    list_ = list(filter(lambda x:len(x)>0, re.findall('[^\d*]*',x)))
    return list_[0] if list_ else np.nan
data_merge['采样点风化类型'] = data_merge['文物采样点'].apply(get_fh)
data_merge['采样点风化类型'].value_counts()
"""
部位       10
未风化点     10
严重风化点     3
Name: 采样点风化类型, dtype: int64
"""

# 第二步
data_merge.replace({'部位':np.nan},inplace=True)
data_merge['采样点风化类型'] = data_merge['采样点风化类型'].fillna(data_merge['表面风化'])
data_merge['采样点风化类型'].value_counts()
"""
风化       29
无风化      25
未风化点     10
严重风化点     3
Name: 采样点风化类型, dtype: int64
"""

# 第三步
data_merge['采样点风化类型'] = data_merge['采样点风化类型'].replace({'无风化':'未风化点', '风化':'风化点'})
data_merge['采样点风化类型'].value_counts()
"""
未风化点     35
风化点      29
严重风化点     3
Name: 采样点风化类型, dtype: int64
"""

展示：

with sns.color_palette('rainbow'):
    # 作者封装绘图程序，需要源程序可在作者博客'seaborn'封装中寻找
    count_pieplot(data_merge,1,2,vars = ['采样点风化类型'],hue = '类型',show_value=True)

问题一：

1、结合玻璃的类型，分析文物样品表面有无风化化学成分的统计规律

        对高钾/铅钡玻璃，统计分析未风化、风化样本的化学成分差异，来探究有无风化化学成分的统计规律，使用折线图、箱线图进行分析，箱线图不仅可以看出样本点化学成分的分布范围，同时能够简明的分析均值、最小最大值。

折线图分析：取出有无风化各化学成分的均值，绘制折线图，观察有无风化化学成分的差异。

# 提取化学名称
def get_huaxue(x):
    return re.findall('\((.*)\)',x)[0]

plt.figure(figsize=(10, 8))
plt.subplot(211)
plt.plot(range(14),data_merge.query("采样点风化类型 == '风化点' & 类型 == '高钾'").iloc[:,6:-1].mean(),label = '风化')
plt.plot(range(14),data_merge.query("采样点风化类型 == '未风化点' & 类型 == '高钾'").iloc[:,6:-1].mean(),label = '未风化')
plt.legend()
plt.xticks(range(14),list(map(get_huaxue, data_merge.iloc[:,6:-1].columns)),fontsize = 10)
plt.title('高钾风化与未风化的各成分均值统计对比图',fontsize = 15)
# plt.savefig('高钾风化与未风化的各成分均值统计对比图')

plt.subplot(212)
plt.plot(range(14),data_merge.query("采样点风化类型 == '风化点' & 类型 == '铅钡'").iloc[:,6:-1].mean(),label = '风化')
plt.plot(range(14),data_merge.query("采样点风化类型 == '严重风化点' & 类型 == '铅钡'").iloc[:,6:-1].mean(),label = '严重风化')
plt.plot(range(14),data_merge.query("采样点风化类型 == '未风化点' & 类型 == '铅钡'").iloc[:,6:-1].mean(),label = '未风化')

plt.legend()
plt.xticks(range(14),list(map(get_huaxue, data_merge.iloc[:,6:-1].columns)),fontsize = 10)
plt.title('铅钡风化与未风化的各成分均值统计对比图',fontsize = 15)
# plt.savefig('风化与未风化的各成分均值统计对比图')
plt.subplots_adjust(hspace=0.35)
plt.savefig('风化与未风化的各成分均值统计对比图')

箱线图分析：分别取出

def get_colors(color_style):
    cnames = sns.xkcd_rgb
    if color_style =='light':
        colors = list(filter(lambda x:x[:5]=='light',cnames.keys()))
    elif color_style =='dark':
        colors = list(filter(lambda x:x[:4]=='dark',cnames.keys()))
    elif color_style =='all':
        colors = cnames.keys()
    colors = list(map(lambda x:cnames[x], colors))
    return colors

# 封装箱线图
def boxplot(data, rows = 3, cols = 4, figsize = (13, 8), vars  =None, hue = None, width = 0.25,
            order = None, color_style ='light',subplots_adjust = (0.2, 0.2)):
    
    fig = plt.figure(figsize = figsize)
    hue = data[hue] if isinstance(hue,str) and hue in data.columns else hue
    data = data if not vars else data[vars]
    
    colors = get_colors(color_style)
    ax_num = 1
    for col in data.columns:
        if isinstance(data[col].values[0],(np.int64,np.int32,np.int16,np.int8,np.float16,np.float32,np.float64)):
            plt.subplot(rows, cols, ax_num)
            sns.boxplot(x = hue,y = data[col].values,color=random.sample(colors,1)[0],width= width,order = order)
            plt.xlabel(col)
#             data[col].plot(kind = 'box',color=random.sample(colors,1)[0])
            ax_num+=1
    
    plt.subplots_adjust(hspace = subplots_adjust[0],wspace=subplots_adjust[1])

# data_merge
data = pd.read_excel('问题一连接两表并处理后数据.xlsx').iloc[:,1:]

boxplot(data.query("类型 == '高钾'"), 4, 4, hue = '采样点风化类型',
        vars = data.columns[1:].tolist(), figsize=(11, 8), subplots_adjust=(0.52,0.25))
plt.savefig('高钾有无风化化学成分箱线图分析.jpg')

高钾：

boxplot(data.query("类型 == '铅钡'"), 4, 4, hue = '采样点风化类型', vars = data.columns[1:].tolist(),
        figsize=(13, 8), subplots_adjust=(0.55,0.25), order = ['未风化点','风化点','严重风化点'])
plt.savefig('铅钡有无风化化学成分箱线图分析.jpg')

 铅钡： 

结合化学元素的描述性统计以及箱线图和折线图可以大致观察出有无风化化学成分的统计规律：

1. 高钾玻璃的二氧化硅含量较高，且风化前后氧化钾以及三氧化二铝成分占比减小，而二氧化硅含量增加，其余化学成分占比变化不大。
2. 铅钡玻璃的二氧化硅占比随着风化程度变大而逐渐减小且减小程度较大，风化前后氧化铅、氧化钡、五氧化二磷含量占比增大，相比较风化数据，严重风化的二氧化硫占比含量增加而风化与未风化的二氧化硫含量相差不大, 其余化学成分占比均变化不大。

2、根据风化点检测数据，预测其风化前的化学成分含量。

     大部分人在这里会卡住，我在第一天晚上就基本上有了第二问思路，并且开始着手第二问的聚类，但却在这一小问的思路上卡到凌晨，队友也没有好的想法，其实一开始我也是明确知道不能使用机器学习方法进行建模，因为很明显没有风化前后的样本匹配点，都是属于不同文物编号的数据，因此不能使用机器学习，在考虑别的方法上花了一点时间，然后想到最简单的统计未风化样本与风化样本的化学成分统计均值比例来得出一个比例系数，然后当预测的时候使用风化后的化学成分乘以这个比例就得到风化前的化学成分含量，这也是答案上提到的‘均值’的方法。

        但是这样直接统计均值的方法不太合适，因为同类型同风化程度玻璃的同个化学成分含量仍然有部分较大差异，如高钾风化采样点数据中某化学成分大部分近似且较小，而存在个别样本点含量很大，导致取均值后均值也较大，不太符合其他大部分数据的情况。

        对于此现象，我们使用正态分布函数对样本点进行加权平均的方式来得到风化前后化学成分变化比例。

from scipy import stats
def zhengtai(x):
    return stats.norm.pdf(x)

# 封装函数，传入高钾或铅钡数据data以及风化采样点类型
def get_mean(data, label):
    d_ = data[data['采样点风化类型'] == label].iloc[:,6:-1].copy()
    # 标准化
    d_scaler = (d_ - d_.mean(axis = 0))/(d_.std(axis = 0))
    # 加权平均
    mean_ = (zhengtai(d_scaler.T).T * d_).sum(axis = 0)/zhengtai(d_scaler.T).T.sum(axis = 0)
    mean_ = mean_.fillna(0)
    # 返回均值与加权均值
    return d_.mean(), mean_

 获取高钾数据均值与加权均值：

a1, a2 = get_mean(data_merge.query("类型 == '高钾'"), '未风化点')
b1, b2 = get_mean(data_merge.query("类型 == '高钾'"), '风化点')

gj_mean = pd.concat((a1,a2,b1,b2),axis = 1)
gj_mean.columns = ['未风化点均值','未风化点加权均值','风化点均值','风化点加权均值']
gj_mean

进行可视化：

d_ = data_merge.query("类型 == '高钾'")
fig, axes = plt.subplots(4,4,figsize = (16,16))
axes = axes.ravel()
for num,fea in enumerate(data_merge.columns[6:-1]):
    sns.stripplot(x = '采样点风化类型',palette = sns.color_palette('deep',3),
                  y = fea,
                  data =d_,ax = axes[num],
                  jitter = True) # ‘抖
    wfh_mean,wfh_mean_jiaquan = gj_mean[['未风化点均值','未风化点加权均值']].loc[fea,:]
    fh_mean, fh_mean_jiaquan = gj_mean[['风化点均值','风化点加权均值']].loc[fea,:]

    color = ['b','r']
    axes[num].plot([-0.5,0.5],[wfh_mean]*2, c = color[0], label = '未风化均值')
    axes[num].plot([-0.5,0.5],[wfh_mean_jiaquan]*2, '--', c = color[0], label = '未风化加权均值')
    
    axes[num].plot([0.5, 1.5], [fh_mean]*2, c = color[1], label = '风化均值')
    axes[num].plot([0.5, 1.5],[fh_mean_jiaquan]*2, '--', c= color[1], label = '风化加权均值')
    if num==1:
        axes[num].legend()
axes[-1].axis('off')
axes[-2].axis('off')
plt.subplots_adjust(0.2,0.2)
plt.show()

 获取铅钡数据均值与加权均值：

a1, a2 = get_mean(data_merge.query("类型 == '铅钡'"), '未风化点')
b1, b2 = get_mean(data_merge.query("类型 == '铅钡'"), '风化点')
c1, c2 = get_mean(data_merge.query("类型 == '铅钡'"), '严重风化点')
qb_mean = pd.concat((a1,a2,b1,b2,c1,c2),axis = 1)
qb_mean.columns = ['未风化点均值','未风化点加权均值','风化点均值','风化点加权均值','严重风化点均值','严重风化点加权均值']
qb_mean

可视化： 

d_ = data_merge.query("类型 == '铅钡'")
fig, axes = plt.subplots(4,4,figsize = (16,16))
axes = axes.ravel()
for num,fea in enumerate(data_merge.columns[6:-1]):
    sns.stripplot(x = '采样点风化类型',palette = sns.color_palette('deep',3),
                  y = fea,
                  data =d_,ax = axes[num], 
                  order = ['未风化点','风化点','严重风化点'],
                  jitter = True) # ‘抖
    
    wfh_mean,wfh_mean_jiaquan = qb_mean[['未风化点均值','未风化点加权均值']].loc[fea,:]
    fh_mean, fh_mean_jiaquan = qb_mean[['风化点均值','风化点加权均值']].loc[fea,:]
    yz_fh_mean, yz_fh_mean_jiaquan = qb_mean[['严重风化点均值','严重风化点加权均值']].loc[fea,:]
    
    color = ['b', 'orange', 'g']
    axes[num].plot([-0.5, 0.5],[wfh_mean]*2, c = color[0], label = '未风化均值')
    axes[num].plot([-0.5, 0.5],[wfh_mean_jiaquan]*2, '--', c = color[0], label = '未风化加权均值')
    
    axes[num].plot([0.5, 1.5], [fh_mean]*2, c = color[1], label = '风化均值')
    axes[num].plot([0.5, 1.5],[fh_mean_jiaquan]*2, '--', c= color[1], label = '风化加权均值')
    
    axes[num].plot([1.5, 2.5],[yz_fh_mean]*2, c = color[2], label = '严重风化均值')
    axes[num].plot([1.5, 2.5],[yz_fh_mean_jiaquan]*2, '--',c = color[2], label = '严重风化加权均值')
    

    axes[num].set_xlabel(None)
    if num==1:
        axes[num].legend()
axes[-1].axis('off')
axes[-2].axis('off')
plt.subplots_adjust(0.2,0.2)
plt.show()

 获取风化前后加权均值比例：

w_gj = (gj_mean.iloc[:,1]/gj_mean.iloc[:,3]).replace({np.inf:0})
w_qb = (qb_mean['未风化点加权均值']/qb_mean['风化点加权均值']).replace({np.inf:0})
w_qb_yz = (qb_mean['未风化点加权均值']/qb_mean['严重风化点加权均值']).replace({np.inf:0})

W = pd.DataFrame([w_gj,w_qb,w_qb_yz],index = ['高钾:风化前后加权比例','铅钡:风化前后加权比例','铅钡:严重风化前后加权比例']).T

 预测：

对风化后的样本点化学成分乘以风化前后比例，即得到风化前化学成分的预测值：

注：但在过程中我们发现还存在一个问题，即当风化采样点某化学成分为0时，不管比例多少相乘的预测结果仍为0，这与未风化采样点的该化学成分大部分情况不一致，若风化后成分为0则风化前预测也只能为0不太符合理想情况，即使未风化采样点中确实有少部分也为0的数据，对此现象我们使用风化前该化学成分的加权均值来作为预测值。

对于预测时风化采样点化学成分为0的处理前后分析：

高钾未风化采样点：

高钾风化采样点：

如上风化前氧化钾含量大部分都含有值且成分也接近10%, 氧化镁也是大部分都含有不为0的较小值。

直接预测： 

 使用风化前加权均值作为预测值：

 如上处理后的结果仍然也在有效范围内，因此作者认为该方法可行，避免了过于死板的预测情况。

高钾预测程序：

# 高钾预测
fh_gj = data_merge.query("类型 == '高钾' &  采样点风化类型 == '风化点'").iloc[:, 6:-1]
fh_gj = fh_gj.replace({0:np.nan})

data_merge.query("采样点风化类型 == '风化点' & 类型 == '高钾'").iloc[:,6:-1]
gj_pred = fh_gj*W['高钾:风化前后加权比例']

gj_pred = gj_pred.fillna(gj_mean['未风化点加权均值'])
# 规整到100% 注：自己分析是否合理
gj_pred = (gj_pred.T/gj_pred.sum(axis = 1)*100).T

# 补上成分外的特征
d_ = data_merge.loc[gj_pred.index,:][['文物编号','纹饰','类型','颜色',
                                                              '表面风化','文物采样点','采样点风化类型']]
gj_pred = pd.concat((d_, gj_pred), axis = 1)

铅钡预测程序： 

# 铅钡预测
fh_qb = data_merge.query("类型 == '铅钡' &  采样点风化类型 == '风化点'").iloc[:, 6:-1]
fh_qb = fh_qb.replace({0:np.nan})

yz_fh_qb = data_merge.query("类型 == '铅钡' &  采样点风化类型 == '严重风化点'").iloc[:, 6:-1]
yz_fh_qb = yz_fh_qb.replace({0:np.nan})

qb_pred = (fh_qb * W['铅钡:风化前后加权比例'])
yz_qb_pred = (yz_fh_qb * W['铅钡:严重风化前后加权比例'])

qb_pred = qb_pred.fillna(qb_mean['未风化点加权均值'])
yz_qb_pred = yz_qb_pred.fillna(qb_mean['未风化点加权均值'])

# 规整到100%
qb_pred = (qb_pred.T/qb_pred.sum(axis = 1)*100).T
yz_qb_pred = (yz_qb_pred.T/yz_qb_pred.sum(axis = 1)*100).T

# 合并风化点与严重风化点预测数据
qb_pred = pd.concat((yz_qb_pred,qb_pred))

# 补上成分外特征
d_ = data_merge.loc[qb_pred.index,:][['文物编号','纹饰','类型','颜色',
                                   '表面风化','文物采样点','采样点风化类型']]
qb_pred = pd.concat((d_, qb_pred), axis = 1)

Result = pd.concat((gj_pred, qb_pred)).reset_index().iloc[:, 1:]
# Result.to_excel('加权平均法预测风化前含量结果.xlsx')
Result

预测结果：随便截图给大家看看  

问题二

1、依据附件数据分析高钾玻璃、铅钡玻璃的分类规律；

箱线图可视化分析高钾、铅钡玻璃化学成分的差异，以探究决定其玻璃类别的分类规律：

# data_merge
data = pd.read_excel('问题一连接两表并处理后数据.xlsx').iloc[:,1:]
# 作者封装函数
boxplot(data,4,4,hue = '类型', vars = data.columns[1:].tolist(),
        figsize=(11, 8), subplots_adjust=(0.52,0.25))
plt.savefig('高钾铅钡玻璃化学成分箱线图分析.jpg')

 密度图分析特征分布

# stat = "count", "frequency", "density", "probability"
def distplot(data, rows = 3, cols = 4, bins = 10, vars = None, hue = None, kind = 'hist',stat = 'count', shade = True,
             figsize = (12, 5), color_style = 'all', alpha = 0.7, subplots_adjust = (0.3, 0.2)):
    assert kind in ['hist', 'kde','both'], "kind must == 'hist' or 'kde'"
    assert stat in ["count", "frequency", "density", "probability"], 'stat must in ["count", "frequency", "density", "probability"]'
    
    fig = plt.figure(figsize = figsize)
    hue_name = hue  if isinstance(hue,str) or hue==None else hue.name
    hue = data[hue] if isinstance(hue,str) and hue in data.columns else hue
    data = data if not vars else data[vars]
    
    colors = get_colors(color_style)
    
    ax_num = 1
    for col in data.columns:
        if isinstance(data[col].values[0],(np.int64,np.int32,np.int16,np.int8,np.float16,np.float32,np.float64)) and col!=hue_name:
            plt.subplot(rows, cols, ax_num)
            if kind == 'hist':
                sns.histplot(x = data.loc[:,col],bins = bins,color=random.sample(colors,1)[0],hue = hue,alpha = alpha,stat = stat)
            elif kind == 'kde':
                sns.kdeplot(x = data.loc[:,col],color=random.sample(colors,1)[0],alpha = alpha,hue = hue,shade = shade)
            else:
                sns.distplot(x = data.loc[:,col],color=random.sample(colors,1)[0],kde=True,bins = bins,)
                plt.xlabel(col)
            ax_num+=1

    plt.subplots_adjust(hspace = subplots_adjust[0],wspace=subplots_adjust[1])

with sns.color_palette('rainbow_r'):
    distplot(data.iloc[:,1:],4,4,kind = 'kde',figsize=(11,7),subplots_adjust=(0.5,0.35),hue = '类型')

       由以上图分析高钾以及铅钡玻璃的二氧化硅、氧化钾、氧化铅、氧化钡、五氧化二磷、氧化锶的特征分布差异较大，特别是氧化铅，高钾的氧化铅含量基本分布在0，而铅钡的氧化铅含量较大，所以这些特征特别是氧化铅很可能是区分高钾以及铅钡的重要特征，随后建立玻璃类型预测模型进行进一步确定以及验证。

        在这里建立的模型可以直接用于问题三预测，问题三主要就是预测结果而已。在这里选择的模型比较简单，数据集体量很小且具有明显的区分特征，使用L1正则逻辑回归、决策树就可以实现高钾、铅钡玻璃的完全区分了，交叉验证精度均达到100%，使用该两个模型的原因不仅在于简单，且具有筛选重要特征的作用，并且可以不受多重共线性的影响，我看很多人使用神经网络，一上来就套用太复杂的模型，我感觉没必要，数据集本身很小且逻辑回归就能满足预测，当然也可以使用随机森林或支持向量机。

        由于该过程很简单，只需按照传统的进行编码以及标准化处理后通过sklearn库进行模型建立，在这里就介绍一下以上思路，就不展示程序了，展示一下几张关于模型的可视化效果图：

   对上图权重图进行分析，我们可以发现其主要决定性因素为二氧化硅、氧化钾、氧化铅、氧化钡等，其中氧化铅权重最大，即其对分类结果的决定性最大，这些影响因素均与箱线图分析中得到的结论一致。

     决策树能对该样本完美分类，由于决策树原理及性质，在此划分条件过于单一，说明氧化铅特征就能区分高钾以及铅钡，且决策边界为线性超平面，如箱线图中氧化铅特征分析中，能够观察到仅需一条直线就能将其区分，只是依据氧化铅含量进行预测，过于依靠单个特征，使得面对噪声等异常数据或者缺少二氧化硅含量的情况下，模型可用性较差，可改用随机森林。

     而逻辑回归与支持向量机均采用了所有特征作为依据进行预测更能达到现实情况中我们想要的效果，考虑支持向量机原理以及上限更高于逻辑回归，因此这里选择最终的模型为支持向量机。

决策平面展示：

2、对于每个类别选择合适的化学成分对其进行亚类划分，给出具体的划分方法及划分结果，并对分类结果的合理性和敏感性进行分析。 

         在这里我们是分别以高钾、铅钡类别的采样点风化类型特征作为聚类依据进行亚分类。依据题意以及数据分析，同一类型玻璃风化前后其化学成分变化较大，因此以将风化、未风化以及严重风化下的玻璃作为亚分类类别，高钾分为未风化、风化两类，铅钡分为未风化、风化、严重风化三类，按照风化程度对原数据样本采样点统计得到以下数据，后续聚类结果评估以此为依据：

 筛选特征：

        筛选特征有多种方式：

        可以通过每个化学成分的离散程度（选择标准差大的特征）作为亚分类的依据，因为对于单个玻璃类型数据，若其某个特征离散程度小，即成分含量近似，则不适合且难以作为进一步划分类别的依据，相反离散程度大的特征，可认为其具有可进一步划分的空间。

        也可以通过分类模型以化学成分作为变量、风化类型作为标签进行训练，然后通过特征的权重大小，或者是特征重要性进行选取特征。在该问题上这种方式可能较好于通过标准差选取的方式，因为由于聚类目的是明确的，筛选特征需考虑筛选特征后的聚类结果更加拟合于风化情况，而标准差大的特征不一定适合作为该聚类的依据特征，反而可能会影响结果。虽然如此，但在第一种方式的基础上仍然可以通过对聚类结果进行分析来稍微调整选择的特征。

随机森林选取特征：

        在这里使用随机森林分类模型进行特征的选取，不使用决策树在于在训练时由于数据集过于简单，很轻易的单个特征就能将其划分，会使得该单特征的重要性为1而其他特征都为0，不能为我们选取多个特征提供依据。

from sklearn.cluster import KMeans, AgglomerativeClustering,DBSCAN
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV 
from sklearn.metrics import f1_score
from sklearn.model_selection import cross_val_score 
from itertools import permutations


data = pd.read_excel('问题一连接两表并处理后数据.xlsx').iloc[:,1:]
d1 = data.query("类型 == '高钾'")
d1.index = range(len(d1))
d2 = data.query("类型 == '铅钡'")
d2.index = range(len(d2))

  高钾：

x = d1.drop('采样点风化类型', axis = 1).iloc[:, 6:]
y = d1['采样点风化类型']

model = RandomForestClassifier()
# 参数调优
parameters = {'max_depth':range(1,5),'min_samples_leaf':[1,2],'criterion':['gini','entropy'],'min_impurity_decrease':[0.01,0.02,0.025]}

grid_search = GridSearchCV(model, parameters,cv=5) 
grid_search.fit(x, y)  # 传入数据

print('网格搜索最高精度为：',grid_search.best_score_)
print('参数最优值：',grid_search.best_params_) 
model.fit(x, y)

gj_fea_df = pd.DataFrame([x.columns,model.feature_importances_],index = ['化学成分','特征重要性']).T
gj_fea_df.sort_values('特征重要性', ascending = False)
"""
化学成分	特征重要性
0	二氧化硅(SiO2)	0.231851
5	氧化铝(Al2O3)	0.170588
2	氧化钾(K2O)	0.146777
3	氧化钙(CaO)	0.138207
6	氧化铁(Fe2O3)	0.097733
10	五氧化二磷(P2O5)	0.096698
7	氧化铜(CuO)	0.034813
4	氧化镁(MgO)	0.02908
8	氧化铅(PbO)	0.017656
11	氧化锶(SrO)	0.017181
12	氧化锡(SnO2)	0.009706
9	氧化钡(BaO)	0.007264
1	氧化钠(Na2O)	0.002448
13	二氧化硫(SO2)	0.0
"""
# 获取降序后的重要性特征列表
gj_fea = gj_fea_df.sort_values('特征重要性', ascending = False)['化学成分'].tolist()

铅钡：

gj_fea = dt.T.loc[:,'高钾（标准差）'].sort_values(ascending = False).index
dt.T.loc[:,'高钾（标准差）'].sort_values(ascending = False)

"""
二氧化硅(SiO2)     14.466726
氧化钾(K2O)        5.307753
氧化钙(CaO)        3.308126
氧化铝(Al2O3)      3.076662
氧化铁(Fe2O3)      1.566033
氧化铜(CuO)        1.492236
五氧化二磷(P2O5)     1.280603
氧化钠(Na2O)       1.088707
氧化钡(BaO)        0.841629
氧化镁(MgO)        0.711802
氧化锡(SnO2)       0.556257
氧化铅(PbO)        0.514144
二氧化硫(SO2)       0.157164
氧化锶(SrO)        0.043866
Name: 高钾（标准差）, dtype: float64
"""

 铅钡：

x = d2.drop('采样点风化类型', axis = 1).iloc[:, 6:]
y = d2['采样点风化类型']

# 参数调优
model = RandomForestClassifier()
parameters = {'max_depth':range(1,5),'min_samples_leaf':[1,2],'criterion':['gini','entropy'],'min_impurity_decrease':[0.01,0.02]}

grid_search = GridSearchCV(model, parameters,cv=5) 
grid_search.fit(x, y)  # 传入数据

print('网格搜索最高精度为：',grid_search.best_score_)
print('参数最优值：',grid_search.best_params_) 
model.fit(x, y)

qb_fea_df = pd.DataFrame([x.columns,model.feature_importances_],index = ['化学成分','特征重要性']).T
qb_fea_df.sort_values('特征重要性', ascending = False)
"""
化学成分	特征重要性
0	二氧化硅(SiO2)	0.227769
8	氧化铅(PbO)	0.207812
3	氧化钙(CaO)	0.092374
10	五氧化二磷(P2O5)	0.087535
11	氧化锶(SrO)	0.06342
5	氧化铝(Al2O3)	0.056736
7	氧化铜(CuO)	0.050561
9	氧化钡(BaO)	0.042228
13	二氧化硫(SO2)	0.03454
4	氧化镁(MgO)	0.033355
2	氧化钾(K2O)	0.030859
1	氧化钠(Na2O)	0.027895
6	氧化铁(Fe2O3)	0.027078
12	氧化锡(SnO2)	0.017839
"""
# 获取铅钡重要性降序特征列表
qb_fea = qb_fea_df.sort_values('特征重要性', ascending = False)['化学成分'].tolist()

筛选特征：通过从特征重要性高到低不断选取特征，并通过聚类后使用f1-score与采样点风化类型进行匹配，量化拟合效果来选取特征，若特征导致下降则删除该特征。

def pinggu_gj(pred):
    score = 0
    for i in permutations([0,1]):
        true1 = d1['采样点风化类型'].replace({'未风化点':i[0],'风化点':i[1]})
        score_ = f1_score(pred, true1, average='weighted')
        score = score_ if score_>score else score
    return score

def pinggu_qb(pred):
    score = 0
    for i in permutations([0,1,2]):
        true2 = d2['采样点风化类型'].replace({'未风化点':i[0], '风化点':i[1], '严重风化点':i[2]})
        score_ = f1_score(pred, true2, average='weighted')
        score = score_ if score_>score else score
    return score

gj_score = 0
qb_score = 0
gj_del_fea = []
qb_del_fea = []
best_gj_fea = []
best_qb_fea = []
for i in range(1, 15):
    fea1 = gj_fea[:i].copy()
    for g in gj_del_fea:
        fea1.remove(g)
    d1_x = d1[fea1]
    
    fea2 = qb_fea[:i].copy()
    for g in qb_del_fea:
        fea2.remove(g)
    d2_x = d2[fea2]
    
    model1 = KMeans( n_clusters=2)
    scaler1 = StandardScaler()
    a1 = scaler1.fit_transform(d1_x)
    y1 = model1.fit_predict(a1)
    d1_['label'] = y1
    if pinggu_gj(d1_['label']) > gj_score: 
        gj_score = pinggu_gj(d1_['label'])
        best_gj_fea = fea1
    else:
        gj_del_fea.append(gj_fea[i-1])
        
    scaler2 = StandardScaler()
    model2 = KMeans( n_clusters=3)
    a2 = scaler2.fit_transform(d2_x)
    y2 = model2.fit_predict(a2)
    d2_['label'] = y2
    if pinggu_qb(d2_['label']) > qb_score:
        qb_score = pinggu_qb(d2_['label'])
        best_qb_fea = fea2
    else:
        qb_del_fea.append(qb_fea[i-1])

        
print(f'高钾数据选择的特征：{best_gj_fea}')
# 高钾数据选择的特征：['二氧化硅(SiO2)', '五氧化二磷(P2O5)']

print(f'铅钡数据选择的特征：{best_qb_fea}')
# 铅钡数据选择的特征：['二氧化硅(SiO2)', '氧化铅(PbO)', '氧化钡(BaO)', '二氧化硫(SO2)']

print(f'高钾f1-score：', gj_score, '铅钡f1-score：', qb_score )
# 高钾f1-score： 0.9435154217762913 铅钡f1-score： 0.8987315891105979

如以上结果：

高钾玻璃选取的特征为：二氧化硅、五氧化二磷

铅钡玻璃选取的特征为：二氧化硅、氧化铅、 氧化钡、 二氧化硫

高钾、铅钡选取的特征聚类结果与原样本的采样点风化类型匹配精度分别为0.94、0.89

使用选取的特征再次聚类，并将聚类结果保存。

对聚类结果进行可视化，分别绘制二维、三维散点图，选取重要性大的2、3个特征作为二维三维的轴（三维绘制中高钾选取的特征只有两个，只需添加其他成分中重要性最大的即可，这里主要是展示大概的聚类效果）。

d1_ = pd.concat((d1.loc[:,['文物编号','类型','文物采样点']], d1.loc[:,'二氧化硅(SiO2)':'二氧化硫(SO2)']),axis = 1)
d2_ = pd.concat((d2.loc[:,['文物编号','文物采样点']], d2.loc[:,'二氧化硅(SiO2)':'二氧化硫(SO2)']),axis = 1)

d1_x = d1[['二氧化硅(SiO2)', '五氧化二磷(P2O5)']]
d2_x = d2[['二氧化硅(SiO2)', '氧化铅(PbO)', '氧化钡(BaO)', '二氧化硫(SO2)']]

# 均值聚类
model1 = KMeans( n_clusters=2)
scaler1 = StandardScaler()
a1 = scaler1.fit_transform(d1_x)
y1 = model1.fit_predict(a1)
d1_['label'] = y1

scaler2 = StandardScaler()
model2 = KMeans( n_clusters=3)
a2 = scaler2.fit_transform(d2_x)
y2 = model2.fit_predict(a2)
d2_['label'] = y2

from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(15,8))

# ax = fig.add_subplot(121, projection='3d')
ax = plt.subplot(121)
for i in range(d1_['label'].nunique()):
    data = d1_[d1_['label']==i]
    ax.scatter(data['二氧化硅(SiO2)'],data['五氧化二磷(P2O5)'],c=colors[i],label =i)
#     ax.scatter(data['二氧化硅(SiO2)'],data['五氧化二磷(P2O5)'],data['氧化铝(Al2O3)'],c=colors[i],label =i)
ax.set_xlabel('二氧化硅(SiO2)')
ax.set_ylabel('五氧化二磷(P2O5)')
# ax.set_zlabel('氧化铝(Al2O3)')
plt.title('高钾:Kmeans聚类结果图',fontsize = 15)
plt.legend()
# plt.savefig('高钾聚类效果三维散点图')


# ax = fig.add_subplot(122, projection='3d')
ax = plt.subplot(122)
for i in range(d2_['label'].nunique()):
    data = d2_[d2_['label']==i]
    ax.scatter(data['二氧化硅(SiO2)'],data['氧化铅(PbO)'],c=colors[i],label =i)
#     ax.scatter(data['二氧化硅(SiO2)'],data['氧化铅(PbO)'],data['氧化钡(BaO)'],c=colors[i],label =i)
ax.set_xlabel('二氧化硅(SiO2)')
ax.set_ylabel('氧化铅(PbO)')
# ax.set_zlabel('氧化钡(BaO)')
plt.title('铅钡:Kmeans聚类聚类结果图',fontsize = 15)
plt.legend()
# plt.savefig('铅钡聚类效果三维散点图')
plt.savefig('Kmeans聚类聚类结果图')
plt.show()

 三维：

层次聚类与均值聚类效果基本一致 。

合理性分析：

如上图高钾三维图中聚成两类，结合样本点风化类型，可知图上二氧化硅含量较高的一类为风化后，另一类含量较低的为风化前数据，符合原数据情况，铅钡玻璃亦如此，如二维三点图中红色点即为严重风化的匹配点，因此认为该聚类结果具有合理性。

敏感性分析：

思路：为探究分类结果的敏感性，我们使用控制变量法，分别对每个特征含量进行范围性变化，期间控制其他特征的含量不变，使用已经训练好的K-means聚类模型对变化后的样本点进行预测，使用f1-score作为指标量化预测结果，若样本点预测结果不变，即分类结果对单个特征变化不敏感，分类结果具有稳定性。

问题三 对附件表单 3 中未知类别玻璃文物的化学成分进行分析，鉴别其所属类型，并对分类结果的敏感性进行分析。

简单分析测试数据的特征分布等情况是否与训练集特征分布差异太大，使用问题二建立的模型对测试数据进行预测即可，使用支持向量机或随机森林的结果都一致。

可视化分析：

def boxplot1(data1,data2, rows = 3, cols = 4,figsize = (13, 8),color_style ='light'):
    fig = plt.figure(figsize = figsize)
    colors = get_colors(color_style=color_style)
    ax_num = 1
    for col in data1.columns:
        if isinstance(data1[col][0],(np.int, np.float)):
            plt.subplot(rows, cols, ax_num)
            data_ = pd.DataFrame([data1[col].values,data2[col].values],index = ['原数据','表单3数据']).T
            sns.boxplot(data = data_,color=random.sample(colors,1)[0],width=0.2,)
#             sns.histplot(data = data_,color=random.sample(colors,1)[0],kde = True)

            plt.xlabel(col)
#             data[col].plot(kind = 'box',color = random.sample(darkcolors,1)[0])
            ax_num+=1
    plt.subplots_adjust(hspace = 0.5)

data3 = data3.fillna(0)
d_ = data_merge.iloc[:,6:-1]

boxplot1(data4,d_,4,4)
plt.savefig('原数据与表单3数据箱线图分析分布情况')
plt.show()

          分别对每个特征含量进行范围性变化，期间控制其他特征的含量不变，使用f1-score作为指标量化预测结果，若样本点预测结果不变，即分类结果对单个特征变化不敏感，分类结果具有稳定性。

文章来源地址https://www.toymoban.com/news/detail-488498.html

到了这里，关于2022全国数学建模-C 题复盘 古代玻璃制品的成分分析与鉴别的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！