PID与ADRC-Toy模板网

这篇具有很好参考价值的文章主要介绍了PID与ADRC。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、 PID算法

1. 定义：

2. PID的意义:

3. P,I,D的控制原理：

3.1. P值的作用：

3.2. D值的作用：

3.3. I值的作用：

3.4. 程序示例：

二、 ADRC算法

1.背景：

2. 原理及组成：

3. 算法特点：

3.1. 几乎和模型无关

3.2. 反应敏捷

一、 PID算法

1. 定义：

PID，就是“比例（proportional）、积分（integral）、微分（derivative）”，是一种很常见的控制算法。常见的PID算法，位置式PID，增量式PID，串级PID等。

2. PID的意义:

以电机转速为例子来解释，电机随着使用时间的增加，电机的性能其实会发生变化，输出相同的PWM值，速度会和最开始测得的值是不一样的。我们有一辆小车（电机控制小车的速度），如果我改变小车的负重，根据生活中的常识，相同的输出电压下，负载越重，小车的速度越慢的。所以说仅仅输出一个PWM值，是不能精确控制电机转动的速度保持在相同的值。这个时候PID的算法就会体现出重要的作用。现在，我用一个编码器来读取电机速度（编码器可以精确读取电机的转动速度），编码器的作用就是把电机转动的速度（模拟量）转化为一个数字量，传入到我们的微处理器。我们使用PID算法本质上是为了让编码器的值（即速度）稳定在一个值。 PID调参变成了如何让编码器的值（速度）保持在一个固定值。

3. P,I,D的控制原理：

简易的PID控制，我们使用PID处理的函数，函数中包括两个参数，一个是编码器测量到当前的速度值（position），另一个就是目标速度值（target）。

3.1. P值的作用：

如果当前的速度值和目标的速度值相差很大，我们就想增大电机的PWM输出，让电机快速达到目标值，PID中的P就扮演着重要的作用，可以联想到PWM=P*（target-position），当前的速度值和目标的速度值相差越大，输出的PWM值就会越大，可以快速达到目标速度值。

PID与ADRC

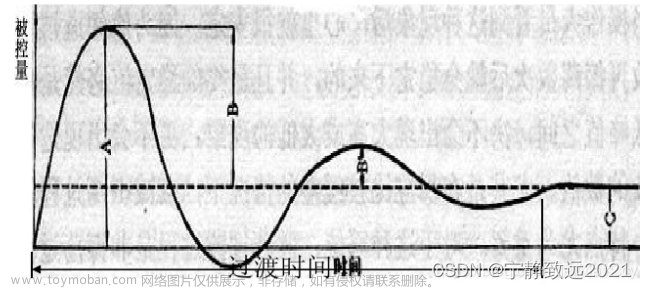
结论：没有积分控制且比例控制较弱时，会出现静差。P值较小情况下，响应速度变慢；P值较大情况下，虽然响应速度比较快，但是震荡严重。

3.2. D值的作用：

PID中的D主要作用于振荡抑制。当比较接近目标时，P的控制作用就比较小了。越接近目标，P的作用越温柔。有很多内在的或者外部的因素，使控制量发生小范围的摆动。

D的作用就是让物理量的速度趋于0，只要什么时候，这个量具有了速度，D就向相反的方向用力，尽力抑制住振荡的变化。

现在我们引入偏差值的概念，令Bia=taget-position，令上一次求得的偏差值为Last_Bia。

D项的计算公式为 D*(Bia - Last_Bia)

举例：现在让当前的速度值为90，目标值为100，Bias=10。现在是为了接近目标值，所以D项的结果是增加PWM。现在增加后的速度变成了105，Bias=-5,Last_Bias=10，Bias-Last_Bias=-15，如果增加后的速度为110，Bias=-10，Last_Bias=10，Bias-Last_Bias=-20，D项的计算结果是为了减小PWM，快速抑制住PWM的过量增加，超过目标值越多，那么抑制能力越厉害。

3.3. I值的作用：

PID中的I的作用是为了消除静差，静差就是指，稳定状态下当前值和目标值的差；

举例：

假如有个人把我们的加热装置带到了非常冷的地方，开始烧水了。需要烧到50℃。在P的作用下，水温慢慢升高。直到升高到45℃时，他发现了一个不好的事情：天气太冷，水散热的速度，和P控制的加热的速度相等了。这可怎么办？P兄这样想：我和目标已经很近了，只需要轻轻加热就可以了。D兄这样想：加热和散热相等，温度没有波动，我好像不用调整什么。于是，水温永远地停留在45℃，永远到不了50℃。

作为一个人，根据常识，我们知道，应该进一步增加加热的功率。可是增加多少该如何计算呢？

设置一个积分量。只要偏差存在，就不断地对偏差进行积分（累加），并反应在调节力度上；

这样一来，即使45℃和50℃相差不太大，但是随着时间的推移，只要没达到目标温度，这个积分量就不断增加。系统就会慢慢意识到：还没有到达目标温度，该增加功率啦！

到了目标温度后，假设温度没有波动，积分值就不会再变动。这时，加热功率仍然等于散热功率。但是，温度是稳稳的50℃。

I 的值越大，积分时乘的系数就越大，积分效果越明显。

I在使用时还有个问题：需要设定积分限制，防止在刚开始加热时，就把积分量积得太大，难以控制。

3.4. 程序示例：

/**************************************************************************
函数功能：位置式PID控制器
入口参数：编码器测量位置信息，目标位置
返回  值：电机PWM
根据位置式离散PID公式 
pwm=Kp*e(k)+Ki*∑e(k)+Kd[e（k）-e(k-1)]
e(k)代表本次偏差 
e(k-1)代表上一次的偏差  
∑e(k)代表e(k)以及之前的偏差的累积和;其中k为1,2,,k;
pwm代表输出
**************************************************************************/

int Position_PID (int position,int target)
{ 	
	 static float Bias,Pwm,Integral_bias,Last_Bias;
	 Bias=target-position;                                  //计算偏差
	 Integral_bias+=Bias;	                                 //求出偏差的积分
	 Pwm=Position_KP*Bias+Position_KI*Integral_bias+Position_KD*(Bias-Last_Bias);       //位置式PID控制器
	 Last_Bias=Bias;                                       //保存上一次偏差 
	 return Pwm;                                           //增量输出
}


/**************************************************************************
函数功能：增量PI控制器
入口参数：编码器测量值，目标速度
返回  值：电机PWM
根据增量式离散PID公式 
pwm+=Kp[e（k）-e(k-1)]+Ki*e(k)+Kd[e(k)-2e(k-1)+e(k-2)]
e(k)代表本次偏差 
e(k-1)代表上一次的偏差  以此类推 
pwm代表增量输出
在我们的速度控制闭环系统里面，只使用PI控制
pwm+=Kp[e（k）-e(k-1)]+Ki*e(k)
**************************************************************************/
int Incremental_PI (int Encoder,int Target)
{ 	
	 static float Bias,Pwm,Last_bias;
	 Bias=Target-Encoder;                                  //计算偏差
	 Pwm+=Velocity_KP*(Bias-Last_bias)+Velocity_KI*Bias;   //增量式PI控制器
	 Last_bias=Bias;	                                   //保存上一次偏差 
	 return Pwm;                                           //增量输出
}

二、 ADRC算法

1.背景：

干扰，或者称扰动，是指系统外部的环境出现变化，或者系统内部特性改变，最终影响了系统的性能。例如上面提到的无人机的螺旋桨，空气阻力随转速变化，影响电机速度的稳定性，这个是外部扰动；当电机长时间运行后，温度明显上升，铜线圈的电阻值升高，原来预估的给多少V电压就得到多少A电流的关系不存在了，这是内部扰动。

来个假设吧，如果世界一切美好、没有任何内外扰动，那么对于任何系统，只要调整好一次PID参数，就可在任何情况下都达到理想效果。但事与愿违，扰动无处不在，如何实现“他强由他强，清风拂山岗；他横由他横，明月照大江”的抗扰动效果，一直是自控工程中最核心的研究工作。

2. 原理及组成：

PID与ADRC

ADRC的核心有三大模块：跟踪微分器、扩张状态观测器和状态误差反馈控制律。

对于电机速度控制，跟踪微分器的输入是目标速度；输出是跟踪速度和跟踪加速度，跟踪速度等于目标速度，跟踪加速度就是目标加速度。

扩张状态观测器的输入分别是：实际速度、输出电压u和系数b0的乘积；输出分别是观测速度、观测加速度和观测扰动，其中观测速度等于实际速度，观测加速度等于实际加速度，观测扰动是系统内部和外部的总扰动，它除以b0后，减去状态误差反馈控制律输出的电压u0，即得到给电机的电压u。

状态误差反馈控制律根据速度误差（跟踪速度-观测速度）、加速度误差（跟踪加速度-观测加速度），输出电压u0，如果两个误差都为零，那么u0为零。系数b0是大致设定的参数，在这里它表示多少V电压对应多少转速RPM。ADRC不管电压和速度的真实关系，它只按自己设定的b0去控制，它认为当前电压是u，速度应该是u*b0，如果实际速度有不同，偏差都认为是扰动（观测扰动），可能是外部阻力变化引起的，也可能是电机内部参数估计不准引起的。观测扰动除以b0后，直接补偿到u输出。所以ADRC就是任性，它无需专门测量扰动，“他自狠来他自恶，我自一口真气足”。

另外，如果系统同时明确：目标速度和目标加速度，那么可以省去跟踪微分器，直接输入这两个量。

3. 算法特点：

3.1. 几乎和模型无关

ADRC适用于从对对象模型一无所知到完全掌握对象模型的任何情况，如图，大致设定电压和速度的关系b0即可。当然如果能准确捕捉到这个关系，ADRC工作强度将减轻，效果更佳。例如我们正在研究，当电机正在运行、发热严重时，电机内部的电阻、电感、反向电动势等参数都明显变化，在不注入额外测量信号下（尽量不影响电机运行），如何利用AI人工智能神经元技术，准确估算电机参数、重构电机模型b0，这样ADRC的性能将更经一步提升。

3.2. 反应敏捷

传统PID控制都要等到误差发生后，才能去补偿控制，而ADRC将观察到的扰动第一时间补偿到输出端。而且PID中的微分项D，虽然说有预测功能，但是它仅仅是将本次的误差减去上一次的误差，得到很粗劣的微分结果，而ADRC使用跟踪微分器，准确跟踪目标值的微分（图示跟踪加速度），以及用扩张状态观测器得出实际值的微分（图示观测加速度），两个相减即为准确的误差微分。

基于PID的FOC控制：

PID与ADRC