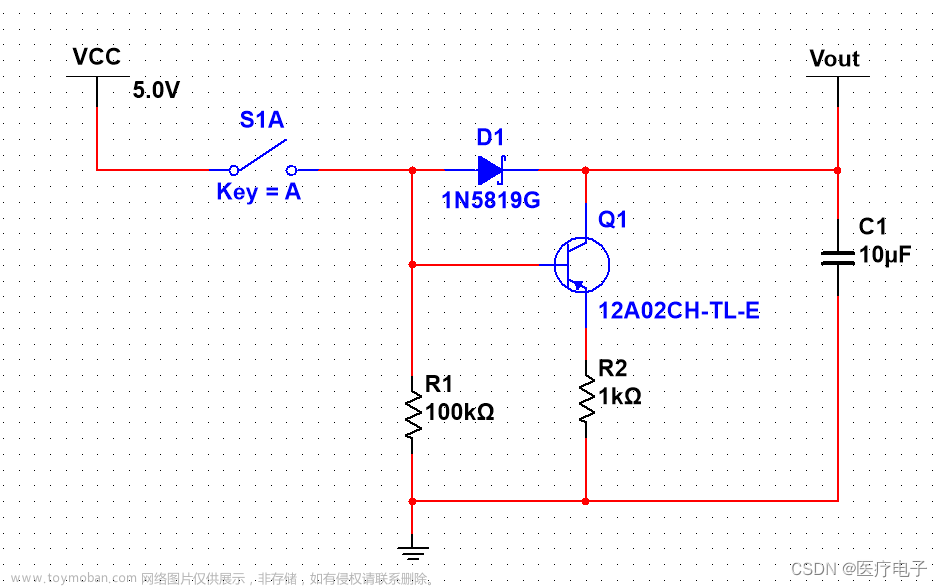
相关知识：
电路：
时间常数：（是指物理量从最大值衰减到1/e所需要的时间）
\tau = RC
对于充电：时间常数是电容器电压 Uc从0增加到63.2% 所需要的时间。
对于放电：时间常数是电容器电压 Uc从Us减少到36.8% 所需要的时间。
电容充放电一般3 - 5个时间常数可以充满电
- 假设有电源Us通过电阻R给电容C充电，U0为电容上的初始电压值，U1为电容充满电后的电压值，Ut为任意时刻(t时)电容上的电压值，那么可以得到以下公式
Ut = U0 + (Us - U0) * (1 - e^-\frac t\tau)
- 如果电容初始电压值为0则公式为
Ut = Us * （1 - e^-\frac t\tau）
- 因为指数值只可能无限接近于0，但永远不会等于0，所以电容电量要完全充满，需要无穷大的时间。 当t = RC时，Vt = 0.63Vu；
当t = 2RC时，Vt = 0.86Vu；
当t = 3RC时，Vt = 0.95Vu；
当t = 4RC时，Vt = 0.98Vu；
当t = 5RC时，Vt = 0.99Vu；
经过3~5个RC后，充电过程基本结束。
RC电路知识补充：
RC动态电路：
零输入响应：换路前电容已充电，即Uc（0+）= Uc（0-）= U0，换路后，电容电压从U0开始逐渐减少，一直下降到0，动态过程结束。
Ut = U0 * e^-\frac t {\tau}
零状态响应：换路前电容状态为0，换路后，电容电压从0开始逐渐增加，直到Ut = Us，动态过程结束
Ut = Us（1 - e^-\frac t \tau）
全响应：换路前电容电压Uc（0-） = U0，换路后，Uc（0+）= Uc（0-） = U0,t趋向于无穷时，电路达到新的稳态，Uc（无穷）= Us。
Ut = U0 * e^-\frac t {\tau} + Us（1 - e^-\frac t \tau）
RC电路的三要素：初值Uc（0+） 、稳态值Uc（无穷）、时间常数
仿真：
1.使用元器件：电阻（RES），电容（CAP），拨码开关（DIPSW）,
2.电路图：
3.示波器现象：（黄色为电源波形，蓝色为电容充电波形）
所用信号频率50hz，的交流脉冲信号，一个周期的时间为0.02s
充满电3-5个时间常数（回顾）
- R1和C1导通时，时间常数为0.00001s，所以几乎可以说是瞬间充满，波形完全重叠
- R1和C2导通，时间常数为0.01s，所以一个周期下来根本充不满
文章来源：https://www.toymoban.com/news/detail-489229.html
- R3和C3导通，时间常数为0.002s，5个时间常数后，一个周期刚好充满
文章来源地址https://www.toymoban.com/news/detail-489229.html
到了这里，关于电路笔记（一）——RC充放电的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
