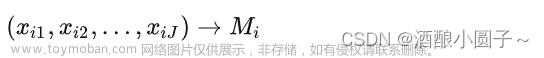数学建模-熵权法-Toy模板网

这篇具有很好参考价值的文章主要介绍了数学建模-熵权法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

熵权法：根据数据本身建立评价体系。
- 什么时候用？
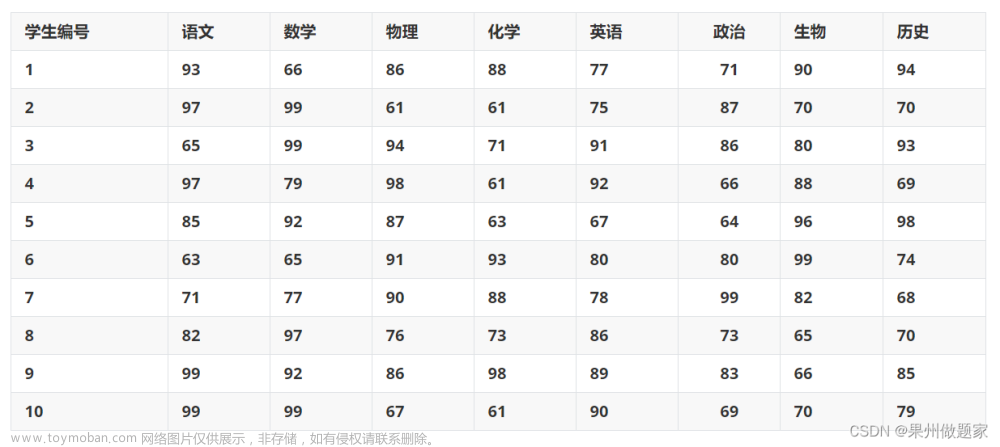
  - 数据全面，缺少文献或主观依据的题目，文献很难帮助我们确定影响水质的哪一个因素最重要，很难告诉我们指标的重要程度如何衡量。追求公平公正。
  - 缺点：难以将数据之外的因素考虑进去
对比（层次分析法、TOPSIS法）最大区别是完全客观
熵（信息熵）：发生的不确定项权：权重。
- 熵权法：利用计算因素或指标的信息熵来确定权重
熵权法流程
- 计算信息熵
  - 数据归一化：把数据压缩到0-1区间内
    - 作用：
      - 消除不同指标之间量纲的影响
      - 正向化，把负向和中间指标变成正向指标
    - 类型：表示我们想要评价的指标在什么情况下最好
      - 正向指标：指标值越大越好
        分母为第j个指标的所有数据的最大值减最小值得到区间长度
        
        分子是得到第j个指标中每个数据在区间的位置
        
        分式的取值是0-1
        
        乘0.999 + 0.001为了让他的区间成为0.001-1
        
        为了让他不包括0，因为计算信息熵的公式中有ln
      - 负向指标：指标值越小越好
        分母一样
        
        举1234的例子就懂了
      - 中间型指标：越靠近中间某个值越好
        M所要评价的区间长度，找到距离最好值的最大值
        
        1-表示负向指标转化为正向指标
        
        用1234来理解
      - 区间型指标
        M计算距离最好值最大的区间长度
        
        ab的区间内表示评价最好
        
        1-还是负向指向正向
  - 计算pij
    - xij就是数据归一化后的值
    - 按这个算
  - 得出信息熵
  - 信息熵冗存度
    - 冗存度和权重才是正比的关系
- 得出权重
- 得出得分
代码：
- 根目录👉🏻数学建模👉🏻MATLAB算法代码👉🏻熵权法
优点
- 操作简单容易上手。
- 通过数据处理直接得到权重，少了主观因素，所得权重更让人信服。
缺点
- 仅由数据波动得出权重，有时候会得到与常理不符的结果
  - 使用熵权法前先对指标进行辨认，去掉与事实不符的指标
  - 与主观性较强的层次分析法结合使用，用层次分析法来验证熵权法的结果
- 归一化手段是线性转换，在最后计算得分时，有些指标的得分不是线性得分
- 要一定量的数据
  - 网络中搜集合适的数据。
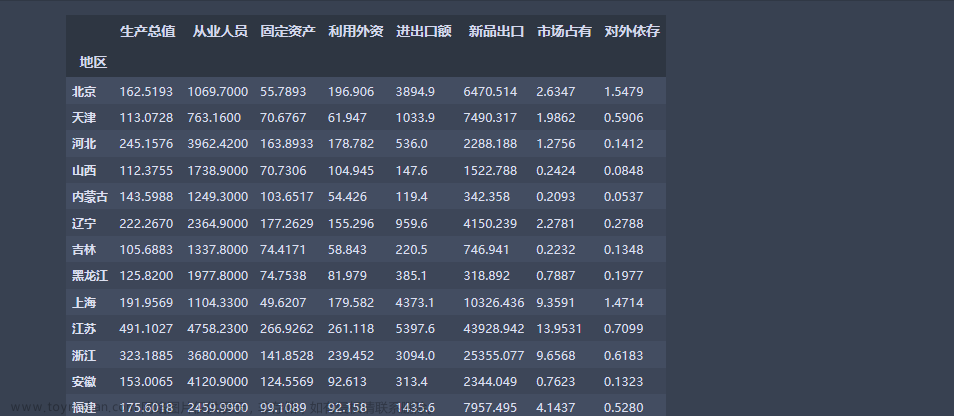
应用
文章来源地址https://www.toymoban.com/news/detail-489592.html