推导过程整理自https://www.bilibili.com/video/BV1s54y1S7Ji。
预备知识
Γ \Gamma Γ函数(伽马函数)
- 定义: Γ ( s ) = ∫ 0 + ∞ e − t t s − 1 d t \Gamma(s)=\int_{0}^{+\infty}e^{-t}t^{s-1}\text{d}t Γ(s)=∫0+∞e−tts−1dt
- 递推公式: Γ ( s + 1 ) = s Γ ( s ) , ( s > 0 ) \Gamma(s+1)=s\Gamma(s),\space(s>0) Γ(s+1)=sΓ(s), (s>0)
- 几个重要的值: Γ ( 1 ) = 1 \Gamma(1)=1 Γ(1)=1, Γ ( 1 2 ) = π \Gamma(\frac{1}{2})=\sqrt{\pi} Γ(21)=π
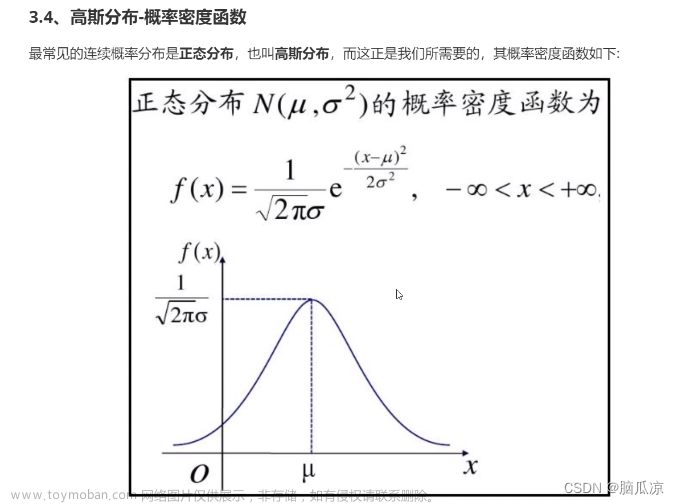
标准正态分布
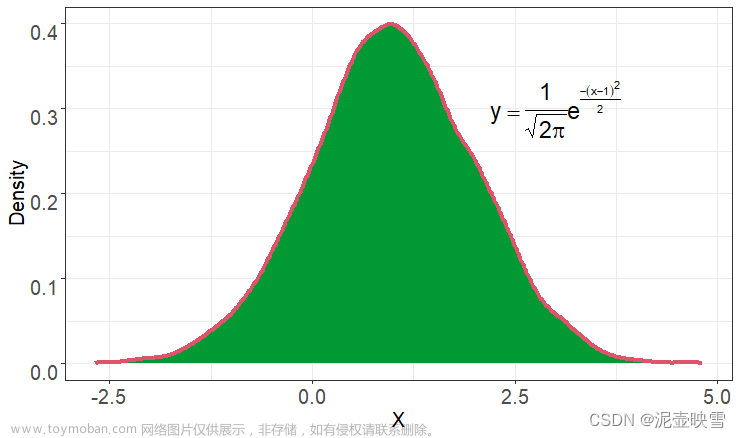
- 概率密度函数: φ ( x ) = 1 2 π e − x 2 2 \varphi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} φ(x)=2π1e−2x2
- 分布函数: ϕ ( x ) = ∫ − ∞ x 1 2 π e − t 2 2 d t \phi(x)=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}\text{d}t ϕ(x)=∫−∞x2π1e−2t2dt
卡方分布
- 概率密度函数: p ( x ) = { 1 2 n / 2 Γ ( n / 2 ) e − x 2 x n 2 − 1 , x > 0 0 , x ⩽ 0 p(x)=\left\{\begin{array}{cc} \frac{1}{2^{n/2}\Gamma(n/2)}e^{-\frac{x}{2}}x^{\frac{n}{2}-1}, & x>0 \\ 0, & x\leqslant 0 \end{array}\right. p(x)={2n/2Γ(n/2)1e−2xx2n−1,0,x>0x⩽0
推导目标
已知 X X X服从标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1), Y Y Y服从卡方分布 χ 2 ( n ) \chi^2(n) χ2(n),且 X X X与 Y Y Y相互独立。
求 T = X Y / n T=\frac{X}{\sqrt{Y/n}} T=Y/nX的概率密度函数。
引理:连续型随机变量商的分布
设
(
X
,
Y
)
(X,Y)
(X,Y)为二维随机变量,其联合密度函数为
p
(
x
,
y
)
p(x,y)
p(x,y),则
Z
=
X
/
Y
Z=X/Y
Z=X/Y的密度函数
p
Z
(
z
)
p_{Z}(z)
pZ(z)满足
p
Z
(
z
)
=
∫
−
∞
+
∞
p
(
z
y
,
y
)
∣
y
∣
d
y
。
p_{Z}(z) = \int_{-\infty}^{+\infty}p(zy, y)|y|\text{d}y \thinspace。
pZ(z)=∫−∞+∞p(zy,y)∣y∣dy。
证明
使用分布函数法,先求 Z Z Z的分布函数,再对分布函数求导得到 p Z ( z ) p_{Z}(z) pZ(z)。
对 z z z的正负性进行讨论,得到积分区域如下图中阴影部分所示。

|

|
我们发现这两种情况可以合并,积分区域均为
{
(
y
,
x
)
∣
y
<
0
∧
x
⩾
z
y
}
\{(y,x) \space|\space y<0 \space\wedge\space x\geqslant zy\}
{(y,x) ∣ y<0 ∧ x⩾zy}
∪
\space\cup\space
∪
{
(
y
,
x
)
∣
y
>
0
∧
x
⩽
z
y
}
\{(y,x) \space|\space y>0 \space\wedge\space x\leqslant zy\}
{(y,x) ∣ y>0 ∧ x⩽zy}。于是有
F
Z
(
z
)
=
P
(
Z
<
z
)
=
P
(
X
Y
<
z
)
=
∫
−
∞
0
d
y
∫
y
z
+
∞
p
(
x
,
y
)
d
x
+
∫
0
+
∞
d
y
∫
−
∞
y
z
p
(
x
,
y
)
d
x
=
x
=
u
y
∫
−
∞
0
d
y
∫
z
+
∞
p
(
u
y
,
y
)
y
d
u
+
∫
0
+
∞
d
y
∫
−
∞
z
p
(
u
y
,
y
)
y
d
u
=
∫
z
+
∞
d
u
∫
−
∞
0
p
(
u
y
,
y
)
y
d
y
+
∫
−
∞
z
d
u
∫
0
+
∞
p
(
u
y
,
y
)
y
d
y
。
\begin{aligned} F_{Z}(z) &\space\space=\space\space P(Z<z) \\ &\space\space=\space\space P(\frac{X}{Y}<z) \\ &\space\space=\space\space \int_{-\infty}^{0}\text{d}y\int_{yz}^{+\infty}p(x,y)\text{d}x + \int_{0}^{+\infty}\text{d}y\int_{-\infty}^{yz}p(x,y)\text{d}x \\ &\overset{x=uy}{=} \int_{-\infty}^{0}\text{d}y\int_{z}^{+\infty}p(uy,y)y\text{d}u + \int_{0}^{+\infty}\text{d}y\int_{-\infty}^{z}p(uy,y)y\text{d}u \\ &\space\space=\space\space \int_{z}^{+\infty}\text{d}u\int_{-\infty}^{0}p(uy,y)y\text{d}y + \int_{-\infty}^{z}\text{d}u\int_{0}^{+\infty}p(uy,y)y\text{d}y \thinspace。 \end{aligned}
FZ(z) = P(Z<z) = P(YX<z) = ∫−∞0dy∫yz+∞p(x,y)dx+∫0+∞dy∫−∞yzp(x,y)dx=x=uy∫−∞0dy∫z+∞p(uy,y)ydu+∫0+∞dy∫−∞zp(uy,y)ydu = ∫z+∞du∫−∞0p(uy,y)ydy+∫−∞zdu∫0+∞p(uy,y)ydy。因此
p
Z
(
z
)
=
F
Z
′
(
z
)
=
−
∫
−
∞
0
p
(
z
y
,
y
)
y
d
y
+
∫
0
+
∞
p
(
z
y
,
y
)
y
d
y
=
∫
−
∞
+
∞
p
(
z
y
,
y
)
∣
y
∣
d
y
。
\begin{aligned} p_{Z}(z) &= F_{Z}'(z) \\ &= -\int_{-\infty}^{0}p(zy,y)y\text{d}y + \int_{0}^{+\infty}p(zy,y)y\text{d}y \\ &= \int_{-\infty}^{+\infty}p(zy,y)|y|\text{d}y \thinspace。 \end{aligned}
pZ(z)=FZ′(z)=−∫−∞0p(zy,y)ydy+∫0+∞p(zy,y)ydy=∫−∞+∞p(zy,y)∣y∣dy。
推导过程
先计算 W = Y / n W=\sqrt{Y/n} W=Y/n 的概率密度函数 p W ( w ) p_{W}(w) pW(w)
同样地,我们使用分布函数法。当
w
⩽
0
w\leqslant 0
w⩽0时,注意到
W
=
Y
/
n
W=\sqrt{Y/n}
W=Y/n恒为非负,所以
P
(
W
<
w
)
=
0
P(W<w)=0
P(W<w)=0,从而
p
W
(
w
)
=
0
p_{W}(w)=0
pW(w)=0。下面针对
w
>
0
w>0
w>0的情况进行计算。
F
W
(
w
)
=
P
(
W
<
w
)
=
P
(
Y
<
n
w
2
)
=
∫
0
n
w
2
1
2
n
/
2
Γ
(
n
/
2
)
e
−
x
2
x
n
2
−
1
d
x
。
\begin{aligned} F_{W}(w) &= P(W<w) \\ &= P(Y<nw^2) \\ &= \int_{0}^{nw^2}\frac{1}{2^{n/2}\Gamma(n/2)}e^{-\frac{x}{2}}x^{\frac{n}{2}-1}\text{d}x \thinspace。 \end{aligned}
FW(w)=P(W<w)=P(Y<nw2)=∫0nw22n/2Γ(n/2)1e−2xx2n−1dx。求导得
p
W
(
w
)
=
F
W
′
(
w
)
=
1
2
n
/
2
Γ
(
n
/
2
)
e
−
n
w
2
2
(
n
w
2
)
n
2
−
1
⋅
2
n
w
=
1
Γ
(
n
/
2
)
2
1
−
n
2
n
n
2
e
−
n
w
2
2
w
n
−
1
。
\begin{aligned} p_{W}(w) &= F_{W}'(w) \\ &= \frac{1}{2^{n/2}\Gamma(n/2)}e^{-\frac{nw^2}{2}}(nw^2)^{\frac{n}{2}-1}\cdot 2nw \\ &= \frac{1}{\Gamma(n/2)}2^{1-\frac{n}{2}}n^{\frac{n}{2}} e^{-\frac{nw^2}{2}}w^{n-1} \thinspace。 \end{aligned}
pW(w)=FW′(w)=2n/2Γ(n/2)1e−2nw2(nw2)2n−1⋅2nw=Γ(n/2)121−2nn2ne−2nw2wn−1。综上,有
p
W
(
w
)
=
{
1
Γ
(
n
/
2
)
2
1
−
n
2
n
n
2
e
−
n
w
2
2
w
n
−
1
,
w
>
0
0
,
w
⩽
0
。
p_{W}(w) = \left\{\begin{array}{cc} \frac{1}{\Gamma(n/2)}2^{1-\frac{n}{2}}n^{\frac{n}{2}} e^{-\frac{nw^2}{2}}w^{n-1}, & w>0 \\ 0, & w\leqslant 0 \end{array}\right. \thinspace。
pW(w)={Γ(n/2)121−2nn2ne−2nw2wn−1,0,w>0w⩽0。文章来源:https://www.toymoban.com/news/detail-489757.html
再计算 T = X W T=\frac{X}{W} T=WX概率密度函数 p T ( t ) p_{T}(t) pT(t)
因为
X
X
X与
Y
Y
Y相互独立,所以
X
X
X与
W
=
Y
/
n
W=\sqrt{Y/n}
W=Y/n也相互独立,于是
(
X
,
W
)
(X,W)
(X,W)的联合概率密度函数
p
(
x
,
w
)
p(x,w)
p(x,w)满足
p
(
x
,
w
)
=
p
X
(
x
)
p
W
(
w
)
。
p(x,w) = p_{X}(x)p_{W}(w) \thinspace。
p(x,w)=pX(x)pW(w)。再根据引理,我们有
p
T
(
t
)
=
∫
−
∞
+
∞
p
(
t
w
,
w
)
∣
w
∣
d
w
=
∫
−
∞
+
∞
p
X
(
t
w
)
p
W
(
w
)
∣
w
∣
d
w
=
∫
0
+
∞
p
X
(
t
w
)
p
W
(
w
)
w
d
w
=
∫
0
+
∞
1
2
π
e
−
t
2
w
2
2
⋅
1
Γ
(
n
2
)
2
1
−
n
2
n
n
2
e
−
n
w
2
2
w
n
−
1
⋅
w
d
w
=
1
π
⋅
Γ
(
n
2
)
2
1
−
n
2
n
n
2
∫
0
+
∞
e
−
n
+
t
2
2
w
2
w
n
d
w
=
w
=
2
z
n
+
t
2
1
π
⋅
Γ
(
n
2
)
2
1
−
n
2
n
n
2
⋅
1
2
(
2
n
+
t
2
)
n
+
1
2
∫
0
+
∞
e
−
z
z
n
−
1
2
d
z
=
Γ
(
n
+
1
2
)
π
⋅
Γ
(
n
2
)
⋅
n
n
2
(
1
n
+
t
2
)
n
+
1
2
=
Γ
(
n
+
1
2
)
n
π
⋅
Γ
(
n
2
)
(
1
+
t
2
n
)
−
n
+
1
2
。
\begin{aligned} p_{T}(t) &\quad\space\,=\quad\space\, \int_{-\infty}^{+\infty}p(tw, w)|w|\text{d}w \\ &\quad\space\,=\quad\space\, \int_{-\infty}^{+\infty}p_{X}(tw)p_{W}(w)|w|\text{d}w \\ &\quad\space\,=\quad\space\, \int_{0}^{+\infty}p_{X}(tw)p_{W}(w)w\text{d}w \\ &\quad\space\,=\quad\space\, \int_{0}^{+\infty} \frac{1}{\sqrt{2\pi}}e^{-\frac{t^2w^2}{2}}\cdot \frac{1}{\Gamma(\frac{n}{2})}2^{1-\frac{n}{2}}n^{\frac{n}{2}} e^{-\frac{nw^2}{2}}w^{n-1}\cdot w\text{d}w \\ &\quad\space\,=\quad\space\, \frac{1}{\sqrt{\pi}\cdot \Gamma(\frac{n}{2})}2^{\frac{1-n}{2}}n^{\frac{n}{2}} \int_{0}^{+\infty}e^{-\frac{n+t^2}{2}w^2}w^n\text{d}w \\ &\overset{w=\sqrt{\frac{2z}{n+t^2}}}{=} \frac{1}{\sqrt{\pi}\cdot\Gamma(\frac{n}{2})}2^{\frac{1-n}{2}}n^{\frac{n}{2}}\cdot \frac{1}{2}(\frac{2}{n+t^2})^{\frac{n+1}{2}} \int_{0}^{+\infty}e^{-z}z^{\frac{n-1}{2}}\text{d}z \\ &\quad\space\,=\quad\space\, \frac{\Gamma(\frac{n+1}{2})}{\sqrt{\pi}\cdot \Gamma(\frac{n}{2})}\cdot n^{\frac{n}{2}}(\frac{1}{n+t^2})^{\frac{n+1}{2}} \\ &\quad\space\,=\quad\space\, \frac{\Gamma(\frac{n+1}{2})}{\sqrt{n\pi}\cdot \Gamma(\frac{n}{2})} (1+\frac{t^2}{n})^{-\frac{n+1}{2}} \thinspace。 \end{aligned}
pT(t) = ∫−∞+∞p(tw,w)∣w∣dw = ∫−∞+∞pX(tw)pW(w)∣w∣dw = ∫0+∞pX(tw)pW(w)wdw = ∫0+∞2π1e−2t2w2⋅Γ(2n)121−2nn2ne−2nw2wn−1⋅wdw = π⋅Γ(2n)1221−nn2n∫0+∞e−2n+t2w2wndw=w=n+t22zπ⋅Γ(2n)1221−nn2n⋅21(n+t22)2n+1∫0+∞e−zz2n−1dz = π⋅Γ(2n)Γ(2n+1)⋅n2n(n+t21)2n+1 = nπ⋅Γ(2n)Γ(2n+1)(1+nt2)−2n+1。推导完毕。文章来源地址https://www.toymoban.com/news/detail-489757.html
到了这里,关于t分布概率密度函数的推导的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!