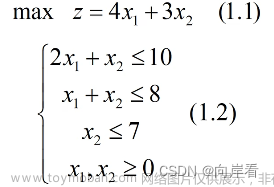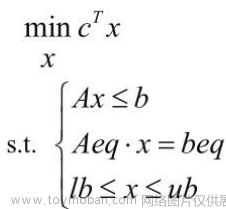目录
1.1 线性规划模型的一般形式:
1.2 线性规划模型
1.1 线性规划模型的一般形式:
- minz=f(x)
- s.t. (i=1,2,···,m)
1和2组成的模型属于约束优化
f(x)称为目标函数,称为约束条件
决策变量、目标函数、约束条件构成了线性规划的3个基本要素
1.2 线性规划模型的矩阵形式:
min u=cx
s.t. Axb
vlb x vub
1.3 线性规划模型
建立线性规划模型的三个基本步骤:
- 找出待定的未知变量(决策变量),用
- 找出问题中所有限制和约束,写出未知变量的线性方程或线性不等式
- 找到模型的目标或判据,写成决策变量的线性函数,以便求出最大值或最小值
例1: 任务分配问题.某车间有甲、乙两台机床,可用于加工三种工件.假定这两台车床的可用台时数分别为800和900.三种工件的数量分别为400,600和500.问怎样分配车床的加工任务,才能既满足加工工件的要求,又使加工费用最低。
| 车床类型 | 单位工件所需加工台时数 | 单位工件的加工费用 | 可用台时数 | ||||
| 工件1 | 工件2 | 工件3 | 工件4 | 工件5 | 工件6 | ||
| 甲 | 0.4 | 1.1 | 1.0 | 13 | 9 | 10 | 800 |
| 乙 | 0.5 | 1.2 | 1.3 | 11 | 12 | 8 | 900 |
解:设在甲机床上加工工件1,2,3的数量为x1,x2,x3,乙机床上加工工件1,2,3的数量为x4,x5,x6.可建立以下线性规划模型:
s.t.
例2: 某厂每日8小时的产量不低于1800件,为了进行质量控制,计划聘请两种不同水平的检验员,且每种检验员的日产量不高于1800件,一级检验员的标准为:速度25 件/h,正确率98%,计时工资4 元/h;二级检验员的标准为:速度 15件/h,正确率95%,计时工资3 元/h.检验员每错检一次,工厂要损失两元.为使总检验费用最省,该工厂应聘一级、二级检验员各几个?
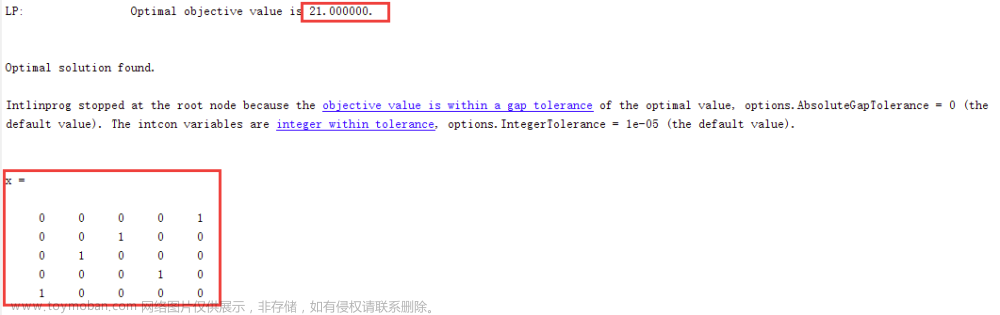
解: 设该工厂应聘一级、二级检验员人数分别为x1,x2
工厂所需支付工资为8×4×x1+8×3×x2=32x1+24x2
因错检造成的损失为(8×25×0.02×x1+8×15×0.05×x2)×2=8x1+12x2
故目标函数为
约束条件为
本问题还应有一个约束条件:x1,x2取整数
注意:
1.在考试时应写全前面的推导过程和建立的线性规划模型,有能力的人可以改写为矩阵形式后编写M文件输出。文章来源:https://www.toymoban.com/news/detail-489853.html
2.编程求解请看线性规划2,将代码放在那里展示了文章来源地址https://www.toymoban.com/news/detail-489853.html
到了这里,关于MATLAB-数学建模-线性规划-1的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!