最小生成树—Prim算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了最小生成树—Prim算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

我们要讨论的问题是如何在一个无向图中找到它的最小生成树，虽然这个问题对有向图也有意义，但是处理起来更麻烦。

一个无向图 G 的最小生成树就是连接 G 上所有顶点的边构成的树，且这些边的总权值最低。当且仅当图是连通的才有最小生成树。

在无向图的最小生成树中，边的条数为。最小生成树是一棵树，因为它无圈；边的总权值最低，所以它最小；包含所有顶点，所以是生成树。显然，最小生成树是包含所有顶点的最小的树。如果我们需要给一所房子里安装电路，那么这就是一个最小生成树问题。

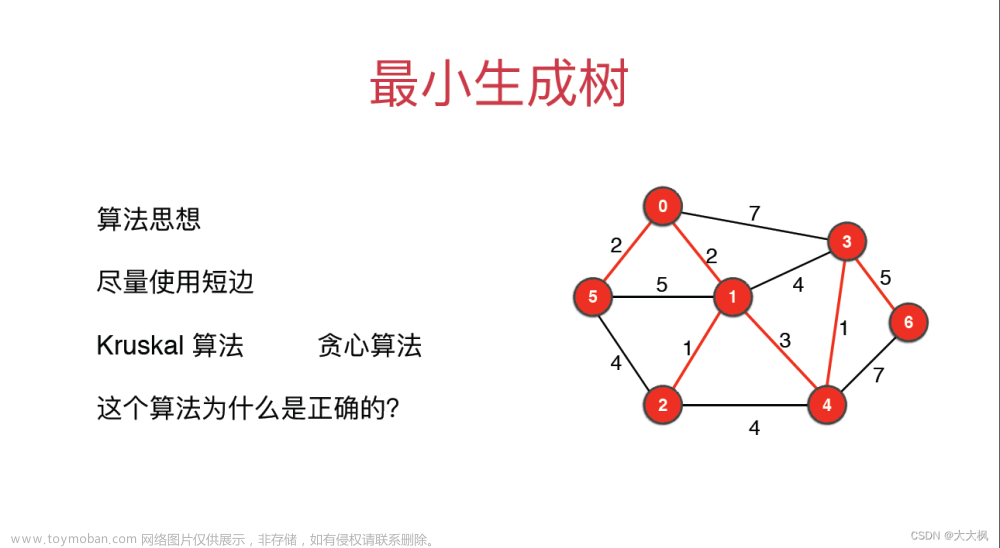
对于任意生成树，如果向树中增加一条不属于树的边，就会形成一个圈，除去圈中任意一条边，又会变回生成树。如果边的值比除去的边值低，那么新的生成树的值就比原树小。如果在建立生成树时所添加的边在所有不成圈的边值中最小，那么最后得到的生成树就不能被改进，否则更改后的树要么成圈，要么权值更高。

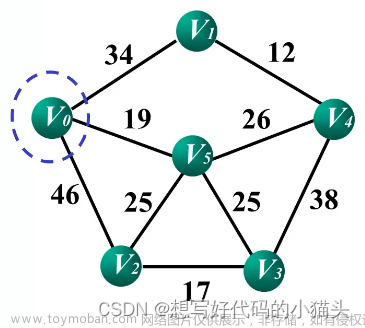
最小生成树的建立方法有两种：Prim算法和Kruskal算法。下面以下图为例，从出发，建立该图的最小生成树。

最小生成树—Prim算法

Prim算法：

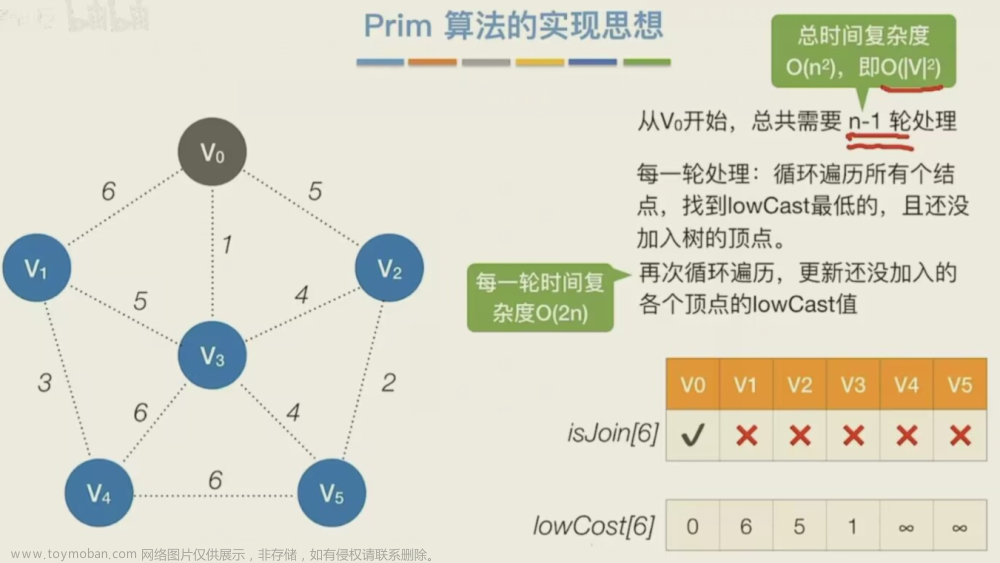
计算最小生成树的方法是使其连续的一步步的成长。在每一步，都要把当前节点当作根节点并往上加边。

Prim算法与Djkstra算法非常相似（Djkstra算法在前一篇文章），在处理当前顶点时，先将其标记为已知，如果的邻接顶点未知，且对应的dvw要小于当前的d，那么就需要更新顶点的d以及path，与Djkstra算法不同的是，d表示的不再是从到输入顶点的距离，而是与邻接顶点的距离，所以其是否更新的判断法则也需要改变。这个算法也是一种贪婪算法，因为在每一步，我们所加入的都是目前权值最小的边，这个算法不会形成圈，因为在算法中不会再改变已知的顶点，并且每一步都将处理顶点视为根节点，所以任何顶点都只能与最后使其d改变的顶点直接相连。

下面说明Prim算法的具体过程，从开始建立最小生成树：

最小生成树—Prim算法

Known	d	path
0	0	-1
0	inf	-1
0	inf	-1
0	inf	-1
0	inf	-1
0	inf	-1
0	inf	-1

与Djkstra算法一样，首先找到d最小的未知顶点，即,将其标记为已知，并更新与它邻接的未知顶点的信息，并且当前更新边中的最小边添加进树（这个操作实际上就是标记该节点为已知，则该节点和其path节点之间的边就被添加进树中，加上边（假设有），总共七条边添加在树中，也就是所有的顶点都被标记为已知，算法就结束）：

最小生成树—Prim算法

Known	d	path
1	0	-1
0	2
0	4
0	1
0	inf	-1
0	inf	-1
0	inf	-1

接下来，d最小的未知顶点是，将其标记为已知，并更新其邻接顶点信息，由于已知，所以不考察，而边的值要大于目前的d，所以的信息不变，但边的值小于目前的d，所以的信息要进行更新，而目前最小的边为，所以将它添加进树：

最小生成树—Prim算法

Known	d	path
1	0	-1
0	2
0	2
1	1
0	7
0	8
0	4

下一个要选择的顶点是，并加入目前的最小边，显然它不会使任何信息改变（除过其自身的Known变为1）。

最小生成树—Prim算法

Known	d	path
1	0	-1
1	2
0	2
1	1
0	7
0	8
0	4

下面要选择的顶点是，对其进行与之前顶点同样的处理：

最小生成树—Prim算法

Known	d	path
1	0	-1
1	2
1	2
1	1
0	7
0	5
0	4

下一步选择的顶点是：

最小生成树—Prim算法

Known	d	path
1	0	-1
1	2
1	2
1	1
0	6
0	1
1	4

接下来选择，并将最小的边加入树中，它不会对任何信息产生影响：

最小生成树—Prim算法

Known	d	path
1	0	-1
1	2
1	2
1	1
0	6
1	1
1	4

最后考察，它也不会对任何信息产生影响：

最小生成树—Prim算法

Known	d	path
1	0	-1
1	2
1	2
1	1
1	6
1	1
1	4

到此，就成功建立了该图的最小生成树，代码如下：

void Prim(g* p) {
	int min, i, Dmin;
	for (;;) {
		Dmin = inf;//找到d最小的未知顶点
		for (i = 0; i < 7; i++) {
			if (p->v[i]->known == 0 && p->v[i]->d < Dmin) {
				min = i;
				Dmin = p->v[i]->d;
			}
		}
		if (Dmin == inf) {//满足这个条件时，要么顶点全部已知，要么图是不连通的
			break;
		}
		p->v[min]->known = 1;
		l* tmp = p->v[min]->next;
		while (tmp != NULL) {
			if (p->v[tmp->val]->known == 0) {
				if (p->v[tmp->val]->d > tmp->dvw) {//判断条件相比Djkstra算法改变
					p->v[tmp->val]->d = tmp->dvw;
					p->v[tmp->val]->path = min;
				}
			}
			tmp = tmp->next;
		}
	}
}

使用两层循环的Prim算法时间复杂度为，当图稠密时，使用这样的方法是好的，如果图是稀疏的，使用二叉堆的时间复杂度为，对于稀疏图来说，这是一个好的界（当图是稠密的，则有，所以使用两层循环是合适的，当图稀疏时，不再满足这个条件，那么的界就比好很多了）。前面提到当且仅当图是连通的才具有最小生成树，判断图是否连通很简单，当程序中最外层的for循环终止后，如果图中仍存在顶点的d=inf，那么就说明图是不连通的。文章来源地址https://www.toymoban.com/news/detail-490129.html

到了这里，关于最小生成树—Prim算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！