主成分分析（PCA）实例讲解-Toy模板网

这篇具有很好参考价值的文章主要介绍了主成分分析（PCA）实例讲解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、什么是主成分分析？

主成分分析（PCA）是一种降维算法，PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分（特征之间互相独立），是在原有n维特征的基础上重新构造出来的k维特征（k<=n），会带来部分信息损失。

二、主成分分析作用？

一般来说，当研究的问题涉及到多变量且变量之间存在很强的相关性时，我们可考虑使用主成分分析的方法来对数据进行简化。

三、主成分分析原理推导

可参考主成分分析原理推导和视频讲解

四、相关问题

1、什么是协方差矩阵？
答:协方差矩阵表示的是两个变量在变化过程中是同向变化（值为正，正相关）还是反向变化（值为负，负相关），变化的程度是多少（值的大小，值为0表示不想关）。协方差公式如下：
主成分分析（PCA）实例讲解
协方差矩阵如下：

协方差矩阵示例：

对数据进行标准化后，每一列数据的期望均为0，此时协方差矩阵可表示为：

2、协方差矩阵特征值为什么可以代表包含信息的多少？
答：协方差矩阵的特征向量表示新坐标轴，特征值表示坐标轴方向的方差，而方差即表示了包含信息的多少。
3、PCA的本质是什么？
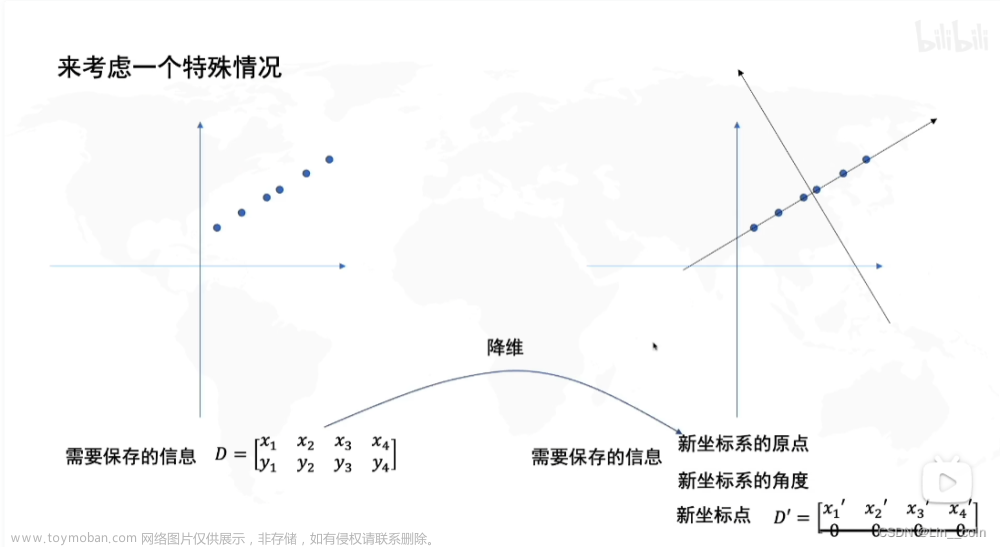
答：PCA的本质其实就是在空间上寻找新的坐标系，使数据在新坐标系下能够尽可能的多保留信息。保留信息的多少用方差来表示，数据越分散，方差越大，信息越多，PCA的作用就是使原有数据在新坐标上方差最大，坐标轴1就是主成分1，坐标轴2就是主成分2，以此类推。
4、PCA的缺点？
答：离群点对于降维结果影响很大

五、PCA公式推导

1、矩阵拉伸变换如下：
主成分分析（PCA）实例讲解
坐标向量表示如下：

拉伸变换前后图像：

2、矩阵旋转变换如下：

坐标向量表示如下：

旋转变换后图像：

3、公式推导：
结合第四节对协方差矩阵的描述内容，对公式进行推导如下：
主成分分析（PCA）实例讲解
其协方差特征值意义如下：

4、求解过程如下：

六、实例讲解

取第三节中数据放入data.xlsx中如下：
主成分分析（PCA）实例讲解
此数据共包含5列15行，即5个维度，先使用sklearn中的PCA模块进行降维，代码如下：

from sklearn.decomposition import PCA
from sklearn.preprocessing import scale
from sklearn.preprocessing import StandardScaler
import pandas as pd

path=r'E:\评分卡逻辑\PCA\data.xlsx'
df=pd.read_excel(path)
data=df.iloc[:,1:]

scale_data=scale(data)
StandardScaler_data=StandardScaler().fit_transform(data)

pca=PCA(n_components=5, copy=True, whiten=False)
pca.fit(scale_data)

newdata=pca.transform(scale_data)

print(pca.explained_variance_)#特征值，即方差
print(pca.explained_variance_ratio_)#占比
print(pca.components_)#特征值对应特征向量