线性变换
线性变换 T \mathcal T T是从向量到向量的映射,并且满足可加性和数乘性: T ( k α + l β ) = k T ( α ) + l T ( β ) \mathcal T(k\alpha+l\beta)=k\mathcal T(\alpha)+l\mathcal T(\beta) T(kα+lβ)=kT(α)+lT(β)
给定一个坐标系后,线性变换 T \mathcal T T对应一个矩阵 A ∈ C m × n \mathbf A\in\mathcal C^{m\times n} A∈Cm×n
- 线性变换的值域Range R ( T ) R(\mathcal T) R(T)就是 A \mathbf A A的列空间 C ( A ) C(\mathbf A) C(A),线性变换的核 N ( T ) N(\mathcal T) N(T)就是 A \mathbf A A的零空间 N ( A ) N(\mathbf A) N(A)
ps. 这里的值域/列空间记为 R R R,而不是 C C C
- 他们仍然满足矩阵四个子空间的结论,例如整个空间
V
=
N
(
T
)
⊕
行空间
(
T
)
V=N(\mathcal T)\oplus 行空间(\mathcal T)
V=N(T)⊕行空间(T),但一般
V
=
N
(
T
)
⊕
R
(
T
)
V=N(\mathcal T)\oplus R(\mathcal T)
V=N(T)⊕R(T)不成立
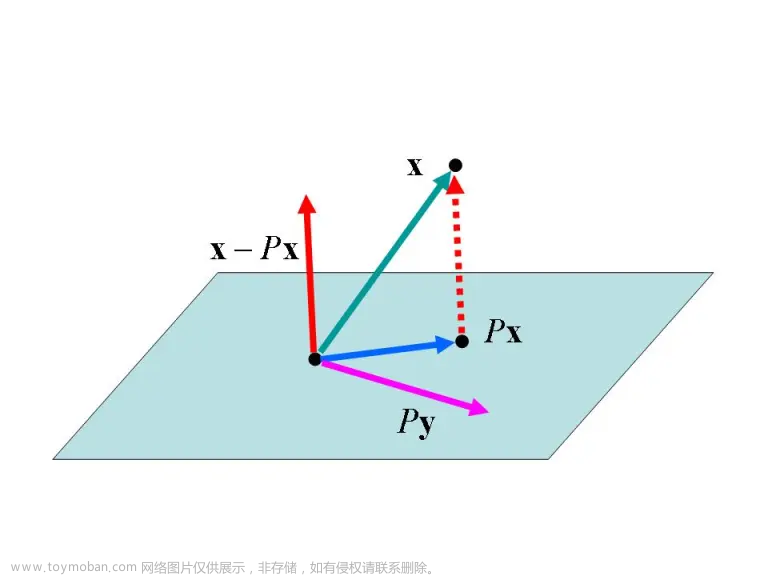
详见线性代数学习笔记4-6:矩阵的四个子空间 - 对于投影变换
T
\mathcal T
T,满足
V
=
N
(
T
)
⊕
R
(
T
)
V=N(\mathcal T)\oplus R(\mathcal T)
V=N(T)⊕R(T)(直和补)
进一步,对于正交投影 T \mathcal T T,满足 N ( T ) ⊥ = R ( T ) N(\mathcal T)^{\bot }= R(\mathcal T) N(T)⊥=R(T)(正交补)
常见的线性变换
在实数域的欧式空间上:
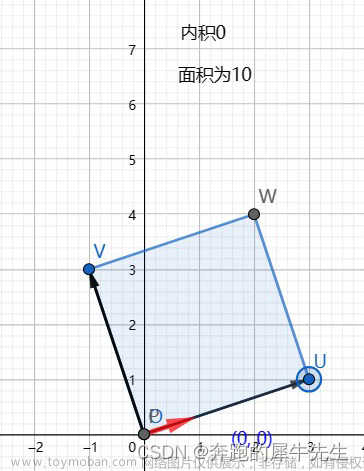
- 正交变换:在一组标准正交基下的矩阵为正交矩阵
特点:特征值 λ \lambda λ满足 ∣ λ ∣ = 1 |\lambda|=1 ∣λ∣=1,且保内积不变 - 对称变换:在一组标准正交基下的矩阵为对称矩阵
特点:特征值全为实数,属于不同特征值的特征子空间(特征向量)互相正交
推广至复数域的酉空间上:
- 酉变换:在一组标准正交基下的矩阵为酉矩阵
- 共轭变换:在一组标准正交基下的矩阵为Hermite矩阵( A H = A \mathbf A^H=\mathbf A AH=A)
具有良好性质的一类变换是正规变换:在一组标准正交基下的矩阵为正规矩阵,满足 A H A = A A H \mathbf A^H\mathbf A=\mathbf A\mathbf A^H AHA=AAH( A \mathbf A A和 A H \mathbf A^H AH都是正规矩阵)
- 特点1:特征向量(
A
x
=
λ
x
\mathbf A\mathbf x={\lambda }\mathbf x
Ax=λx)满足
A
H
x
=
λ
ˉ
x
\mathbf A^H\mathbf x=\bar{\lambda }\mathbf x
AHx=λˉx
或者说,正规变换 A \mathbf A A与正规变换 A H \mathbf A^H AH的特征向量完全相同(且特征值互为共轭) - 特点2:正规矩阵
A
\mathbf A
A是单纯矩阵(可相似对角化),并且与对角阵酉相似(
A
=
U
Λ
U
H
\mathbf A=\mathbf U\mathbf \Lambda\mathbf U^H
A=UΛUH)
另外,根据特点1,正规矩阵 A H = U Λ H U H = U Λ ˉ U H \mathbf A^H=\mathbf U {\mathbf \Lambda}^H\mathbf U^H=\mathbf U \bar{\mathbf \Lambda}\mathbf U^H AH=UΛHUH=UΛˉUH(与前面是相同的 U \mathbf U U和 Λ \mathbf \Lambda Λ) - 特点3:正规变换/正规矩阵 属于不同特征值的特征子空间(特征向量)互相正交
证明:
对于对称矩阵 A \mathbf A A,两个不同的特征向量满足 A x = λ x , A y = α y ( λ ≠ α ) \mathbf A\mathbf x=\lambda \mathbf x,\mathbf A\mathbf y=\alpha \mathbf y(\lambda\neq\alpha) Ax=λx,Ay=αy(λ=α)
目标:构造内积 ( x , y ) = x H y = 0 (\mathbf x,\mathbf y)=\mathbf x^H\mathbf y=0 (x,y)=xHy=0
①由 A x = λ x \mathbf A\mathbf x=\lambda \mathbf x Ax=λx,转置得 x H A H = λ ˉ x H \mathbf x^H\mathbf A^H=\bar\lambda\mathbf x^H xHAH=λˉxH,故 x H A H y = λ ˉ x H y \mathbf x^H\mathbf A^H\mathbf y=\bar\lambda\mathbf x^H\mathbf y xHAHy=λˉxHy
②由 A y = α y \mathbf A\mathbf y=\alpha \mathbf y Ay=αy,结合上共轭矩阵的性质得 A H y = α ˉ y \mathbf A^H\mathbf y=\bar{\alpha}\mathbf y AHy=αˉy,故 x H A H y = α ˉ x H y \mathbf x^H\mathbf A^H\mathbf y=\bar{\alpha}\mathbf x^H\mathbf y xHAHy=αˉxHy
结合①②可知 λ ˉ x H y = α ˉ x H y \bar\lambda\mathbf x^H\mathbf y=\bar{\alpha}\mathbf x^H\mathbf y λˉxHy=αˉxHy,即 ( λ ˉ − α ˉ ) x H y = 0 (\bar\lambda-\bar{\alpha})\mathbf x^H\mathbf y=0 (λˉ−αˉ)xHy=0而 λ ≠ α \lambda\neq\alpha λ=α,故 x T y = 0 \mathbf x^T \mathbf y=0 xTy=0,即两特征向量正交,由 λ \lambda λ和 α \alpha α的任意性可知,正规矩阵属于不同特征值的特征向量必正交
正交变换、对称变换、反对称变换都是正规变换
不变子空间(invariant subspace)
不变子空间的概念是针对特定的线性变换
T
\mathcal T
T而言的:
对于子空间
V
1
=
s
p
a
n
(
α
1
,
.
.
.
,
α
r
)
V_1=span(\bold{\alpha_1,...,\alpha_r})
V1=span(α1,...,αr),
T
(
α
i
)
∈
V
1
,
i
=
1
,
2
,
.
.
.
,
r
\mathcal T(\bold{\alpha_i})\in V_1,i=1,2,...,r
T(αi)∈V1,i=1,2,...,r(该空间的任意基向量做线性变换
T
\mathcal T
T,仍属于该空间)
⟺
\iff
⟺
V
1
V_1
V1是线性变换
T
\mathcal T
T的不变子空间
或者说:不变子空间 V 1 V_1 V1内的任意向量 x \bold x x,都满足 T ( x ) ∈ V 1 \mathcal T(\bold{x})\in V_1 T(x)∈V1
(任意向量都可以表示为基向量的线性组合,结合上线性变换的可加性与数乘性,即可证明)
不变子空间是一个特殊的线性子空间,该子空间中的任意向量 x \bold x x经过线性变换 T \mathcal T T后,仍然在该子空间内
不变子空间的性质:
- 最典型的不变子空间:
线性变换 T \mathcal T T的任意特征值 λ \lambda λ的特征子空间 V λ = { x ∣ T x = λ x } V_\lambda =\{x|\mathcal Tx=\lambda x\} Vλ={x∣Tx=λx},都是 T \mathcal T T的不变子空间
i.e. 特征值 λ i \lambda_i λi对应的特征向量的张成空间是不变子空间,特征值分解 A = V Λ V − 1 \mathbf A =\mathbf V \mathbf \Lambda \mathbf V^{-1} A=VΛV−1中 V \mathbf V V的相应列就给出了该不变子空间的一组基(特别的,对于对称阵 A \mathbf A A, V \mathbf V V给出的是一组正交基);
当特征值 λ i \lambda_i λi为唯一的,则对应一个一维不变子空间,基就是特征向量本身;
对于高维不变子空间,基底不唯一文章来源:https://www.toymoban.com/news/detail-491130.html
- 线性变换 T \mathcal T T有多个不变子空间,这些不变子空间的交/这些不变子空间的和,仍为不变子空间
推论: V 1 V_1 V1是线性变换 T \mathcal T T的不变子空间,那么 V 1 V_1 V1也是任何多项式 f ( T ) f(\mathcal T) f(T)的不变子空间
推论: V 1 V_1 V1同时是线性变换 T 1 \mathcal T_1 T1和 T 2 \mathcal T_2 T2的不变子空间,那么 V 1 V_1 V1也是 T 1 + T 2 \mathcal T_1+\mathcal T_2 T1+T2及 T 1 T 2 \mathcal T_1\mathcal T_2 T1T2的不变子空间文章来源地址https://www.toymoban.com/news/detail-491130.html
- 值域 R ( T ) R(\mathcal T) R(T)和核 N ( T ) N(\mathcal T) N(T)都是线性变换 T \mathcal T T的不变子空间(用定义可验证)
到了这里,关于矩阵理论| 基础:线性变换(正交/酉变换、对称/共轭变换、正规变换)、不变子空间的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!