day57|动态规划17-最长回文子串问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了day57|动态规划17-最长回文子串问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

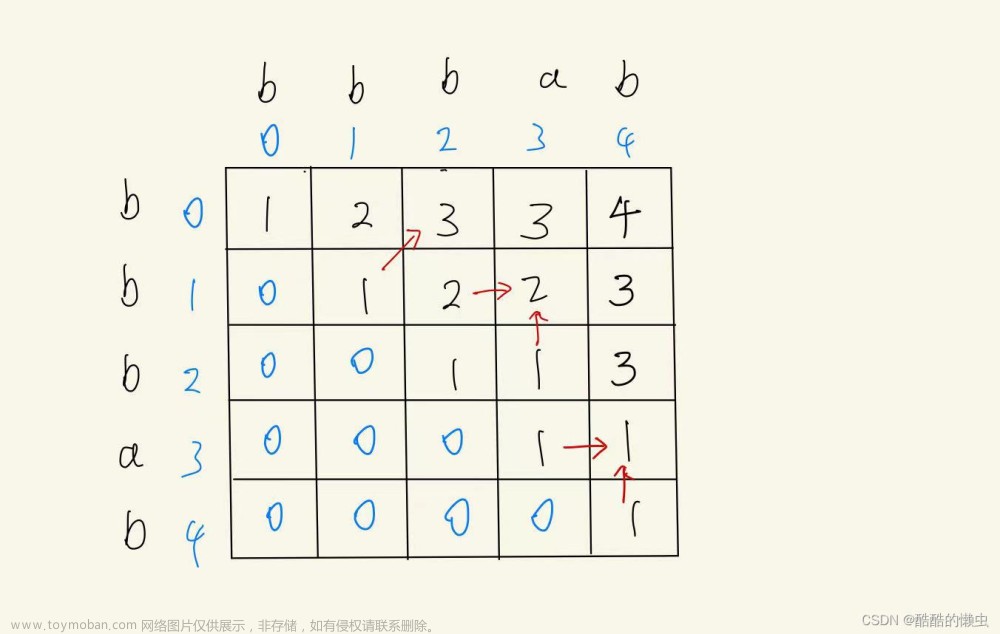
回文子串：强调连续
回文子序列：不强调连续

647. 回文子串的个数

day57|动态规划17-最长回文子串问题

暴力思路：三层for循环
双指针思路：
动态规划
dp数组

dp[i][j]： 根据字符串的形式和所解决的问题确定dp数组的形式和含义。
递归公式（分情况讨论）
2.1 如果 ij
2.2 如果 j-i1
2.3 如果 j-i>1: 此时依赖于dp[i+1][j-1]是不是一个回文子串，当dp[i+1][j-1]为一个回文子串时，那么外层也就是一个回文子串。外层利用result记录回文子串的个数。
初始化：默认都不是回文子串
遍历顺序： 从底往上，从左到右进行遍历（再确定遍历顺序的时候，一定要搞清楚后一个状态与前一个状态的以来依赖关系，依赖关系决定了元素的遍历顺序。并且要控制j应该是大于等于i的。
输出结果

class Solution:
    def countSubstrings(self, s: str) -> int:
    	# dp[i][j]表示字符串i-j之间的字符串是否为回文子串
        s = list(s)
        row,col = len(s),len(s)
        dp = [[False]*col for _ in range(row)]
        result = 0
        for i in range(row-1,-1,-1):
            # j的取值一定是大于或者等于i的所以在第2个循环中需要初始化j的取值为i
            for j in range(i,col):
                if s[i] == s[j]:
                    if j-i<=1: dp[i][j] = True
                    else: dp[i][j] = dp[i+1][j-1]
                    if dp[i][j] : result += 1
        return result

516.最长回文子序列

元素不连续应该怎么分析呢？

dp[i][j] 表示i-j这个范围内的回文子序列的长度
递推公式： 如何得到i-j之间的回文子序列的长度，还是先比较s[i]和s[j]是否相同。
2.1 如果s[i]==s[j] 那么最长回文子序列的长度取决于内部的情况dp[i+1][j-1]+2
2.2 如果s[i]!=s[j] 那么可以分为两种分别考虑s[i]和s[j]的情况，因为考虑的是最长回文子序列，所以取max即可。
初始化： dp[i][i]=1，在相同的子串时的状态应该初始化为1
遍历顺序： 从下向上进行遍历
打印dp数组

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        # dp表示i-j之间的最大回文子串有多少个
        s = list(s)
        row,col = len(s),len(s)
        dp = [[0]*row for _ in range(col)]
        for i in range(row):
            dp[i][i] = 1
        for i in range(row-1,-1,-1):
            for j in range(i+1,col,1):
                if s[i] == s[j]:
                    dp[i][j] = dp[i+1][j-1] + 2
                else:
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1])
        # 最后一个状态的元素是[0][-1]
        return dp[0][-1]