目录
大学生恋爱数据分析报告
一、研究目的
二、数据来源和相关说明
三、描述性统计分析
3.1 基本情况
(1)年级、性别、家乡情况
(2)身高、体重情况
3.2 恋爱情况
(1)恋爱比例
(2)恋爱史
3.3 职务担任情况
3.4 运动情况
3.5 才艺情况
3.6 颜值情况
3.7 生活规划情况
3.8 变量间的相关性
(1)连续型变量热力图
(2)连续变量与是否恋爱的关系
四、数据建模
4.1 全模型
(1)模型建立
(2)结果预测
4.2 基于AIC准则下的选模型A
4.3 基于BIC准则下的选模型B
4.4 模型评估
五、结论及建议
5.1 结论
5.2 建议
六、代码
大学生恋爱数据分析报告
内容提要:本文依据“大学生恋爱数据”,对大学生恋爱状况和恋爱影响因素进行分析。被调查的学生中,大四学生最多,男女比例基本一致,大部分学生来自于二三线城市,身高介于155-185cm之间,体重介于40-70kg之间。被调查学生中,72%的人恋爱,大部分人被别人追求过且为党员,且会跑步、打羽毛球、吹乐器和唱歌。用全模型对第一个受访者的恋爱状况进行预测时,分界点α=0.5 时判断正确,α=0.3 时判断错误。是否追求过别人、是否被别人追求过、寝室同学是否谈过恋爱和每月话费对是否恋爱由显著影响。结合ROC曲线和AUC值可以得出,三个模型中AIC模型分类效果最好。
一、研究目的
近年来,老龄化愈发严重,新生儿出生率显著降低。婚姻是生育的前提,探究现代人的婚恋观具有重要意义。00后婚恋观与以往发生了较大变化,计划终生不婚在00后中较为常见,调研青年人婚恋观的影响因素,对于提升生育率有重要意义。本文旨在依据“大学生恋爱数据”,分析大学生恋爱现状,进而得出大学生恋爱的影响因素。
二、数据来源和相关说明
数据来源于“大学生恋爱数据”文件,据此分析大学生恋爱现状与影响因素。数据共包含32个变量,包括一个因变量和31个自变量。根据变量的含义,将31个变量分为了七类——基本信息、恋爱情况、职务情况、运动情况、才艺情况、颜值情况和生活规划情况。由于变量较多,本文用给定的符号代表这些变量,具体符号与变量解释如表2-1所示。
表2-1 变量解释与符号
| 变量 |
解释 |
符号 |
变量 |
解释 |
符号 |
| 是否恋爱 |
0-否;1-是 |
Y |
唱歌 |
0-否;1-是 |
CY1 |
| 年级 |
1-大一;2-大二; 3-大三;4-大四 |
JB1 |
主持 |
0-否;1-是 |
CY2 |
| 性别 |
0-男;1-女 |
JB2 |
舞蹈 |
0-否;1-是 |
CY3 |
| 家乡 |
1-一线城市;2-二线城市; 3-三线城市;4-县级市; 5-农村 |
JB3 |
乐器 |
0-否;1-是 |
CY4 |
| 身高 |
连续变量 |
JB4 |
其他才艺 |
0-否;1-是 |
CY5 |
| 体重 |
连续变量 |
JB5 |
是否戴眼镜 |
0-否;1-是 |
YZ1 |
| 是否追求过别人 |
0-否;1-是 |
LA1 |
颜值 |
连续变量 |
YZ2 |
| 是否被别人追求过 |
0-否;1-是 |
LA2 |
每周自习时间 |
连续变量 |
GH1 |
| 寝室同学是否谈过恋爱 |
0-否;1-是 |
LA3 |
每周娱乐时间 |
连续变量 |
GH2 |
| 班干部 |
0-否;1-是 |
ZW1 |
每周睡觉时间 |
连续变量 |
GH3 |
| 党员 |
0-否;1-是 |
ZW2 |
每周运动时间 |
连续变量 |
GH4 |
| 足球 |
0-否;1-是 |
YD1 |
每月话费 |
连续变量 |
GH5 |
| 篮球 |
0-否;1-是 |
YD2 |
学生组织个数 |
连续变量 |
GH6 |
| 乒乓球 |
0-否;1-是 |
YD3 |
成绩水平 |
连续变量 |
GH7 |
| 羽毛球 |
0-否;1-是 |
YD4 |
生活费_百元 |
连续变量 |
GH8 |
| 跑步 |
0-否;1-是 |
YD5 |
|||
| 台球 |
0-否;1-是 |
YD6 |
三、描述性统计分析
为了获得对数据的整体了解,本文先对数据进行了描述性统计分析。考虑到变量较多,本文从基本情况、恋爱情况、职务情况、运动情况、才艺情况、颜值情况、生活规划情况和变量间的相关性八个方面对数据进行可视化。
3.1 基本情况
为了分析学生基本情况,本文绘制了饼图和直方图,分别如图3-1和3-2所示。
(1)年级、性别、家乡情况
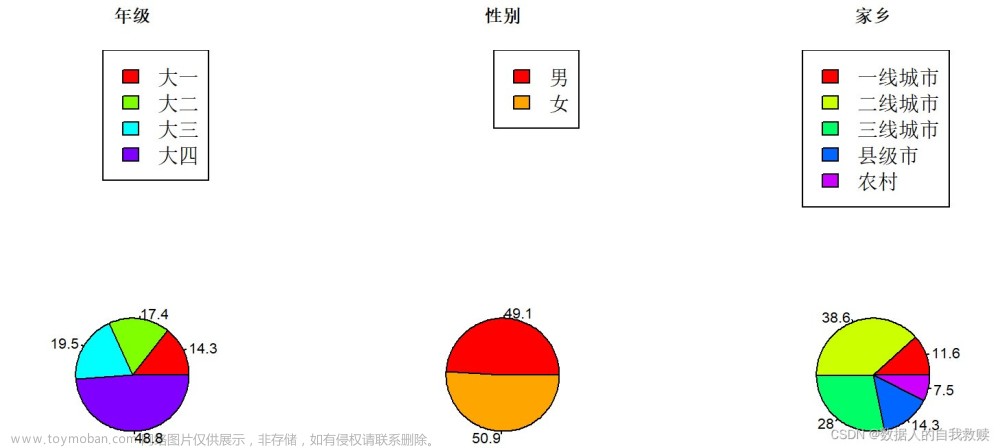
图3-1 学生基本情况饼图
由图3-1可以得出:
- 被调查的学生中,大一到大三年级人数较少,占比在14%~20%之间内,大四人数最多,约占到被调查学生的一半,占比48.8%。
- 男生占比49.1%,女生占比50.9%,男女比例基本符合1:1。
- 家乡来源中,二线城市人数最多,占比38.6%,其次为三线城市和县级市,分别占比28%和14.3%,农村人数最少,仅占比7.5%。
(2)身高、体重情况
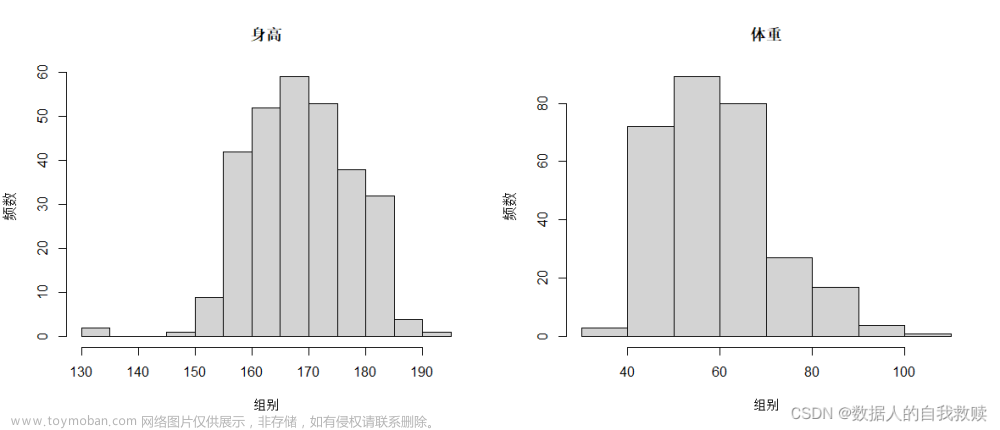
图3-2 学生身高、体重直方图
由图3-2可以得出:
- 学生身高在165cm-170cm频数最高,大部分学生的身高集中在155cm-185cm范围内,学生的身高状况大致服从正态分布。
- 学生体重在50kg-60kg频数最高,大部分学生的体重集中在40kg-70kg范围内,学生的体重状况也大致服从正态分布。
3.2 恋爱情况
(1)恋爱比例
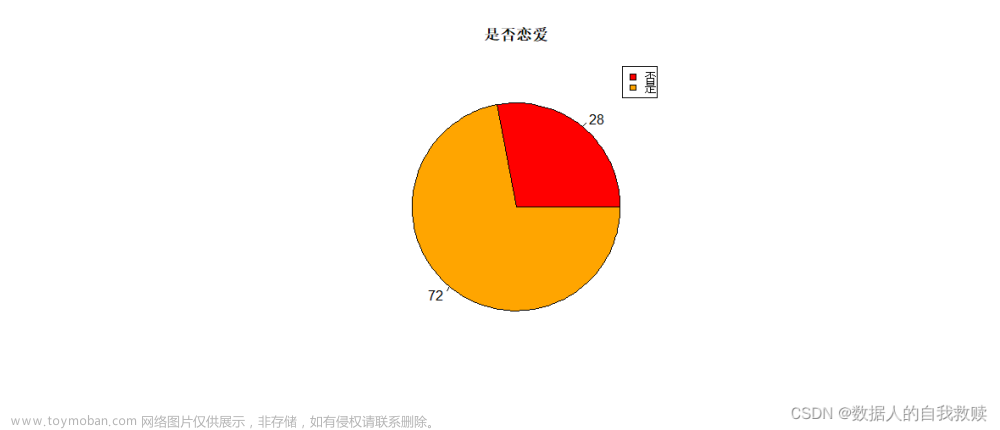
图3-3 是否恋爱饼图
由图3-3可以得出:被调查的大学生中,72%的学生在恋爱,只有28%的学生未恋爱,即大学生恋爱比例还是相对较高的。
(2)恋爱史

图3-4 学生恋爱史饼图
由图3-4可以得出:
- 有54.3%的学生追求过别人,45.7%的学生没有追求过别人,追求过别人的人占总人数的一半以上。
- 有74.7%的学生被别人追求过,25.6%的学生没有被别人追求过,较大部分学生被别人追求过。
- 有70%的同学寝室同学没有谈过恋爱,有30%的同学寝室同学没有谈过恋爱,寝室同学谈过恋爱的同学占比较少。
3.3 职务担任情况

图3-5 职务担任情况饼图
由图3-5可以得出:学生中65.6%是班干部,81.6%是党员,班干部学生占比一半以上,学生证大部分都是党员。
3.4 运动情况
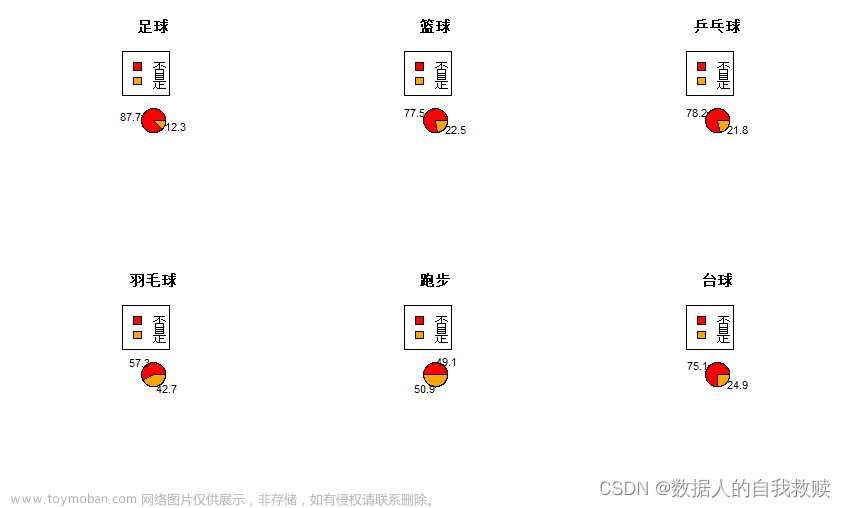
图3-6 学生运动情况饼图
由图3-6可以得出:跑步、羽毛球和台球比较受被调查大学生的欢迎,分别占比50.9%、42.7和24.9;足球最不受被调查大学生的欢迎,占比仅为12.3%。
3.5 才艺情况
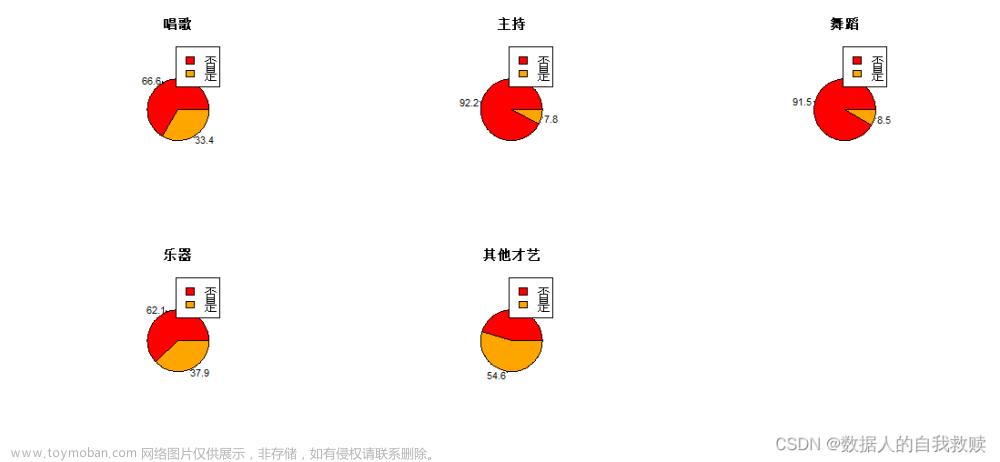
图3-7 学生才艺情况饼图
由图3-7可以得出:学生中会其他才艺、乐器和唱歌的人数较多,分别占比54.6%、37.9%和33.4%,学生中会主持和舞蹈的人数较少,仅占比8%~9%。
3.6 颜值情况
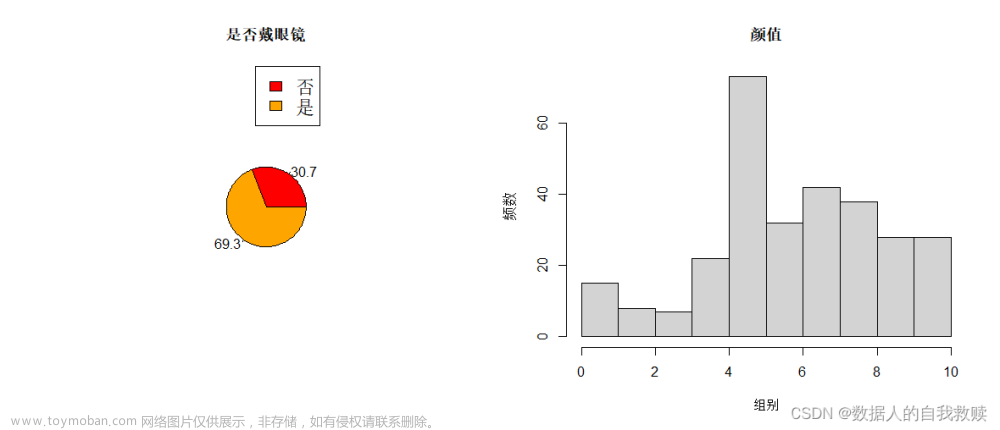
图3-8 学生颜值状况
由图3-8可以得出:69.3%的学生均佩戴眼镜,占总人数的一半以上;学生的颜值在4-5分之间人数最多,远远多于其他组颜值;相较于低颜值,高颜值人群人数要多于低颜值人群,即人群整体颜值集中在4-10分,极低颜值人数较少。
3.7 生活规划情况

图3-9 学生生活规划情况
由图3-9可以得出:学生每周自习时间集中在0-20h,其中5-10h与15-20h人数最多;学生每周娱乐时间集中在0-30和,其中0-10h人数最多;学生每周睡觉时间集中在40-60h,其中50-60h人数最多;学生每周运动时间集中在0-10h,其中0-5h人数最多;学生每月话费集中在30-60元和90-100元,其中90-100元人数最多;学生组织个数集中在0.5-1、1.5-2和2.5-3,其中2.5-3人数最多;学生成绩水平分布较为均匀,其中40-50分人数最多;学生生活费集中在0-3000元,其中1000-2000元人数最多。
3.8 变量间的相关性
(1)连续型变量热力图

图3-10 相关性热力图
由图3-10可以得出:除了身高和体重间的相关性外,其他各个变量间的相关性非常弱。身高和体重的相关系数为0.75,属于中强度正相关关系,其他变量间的相关系数绝对值均不超过0.25,因而相关关系非常弱。
(2)连续变量与是否恋爱的关系
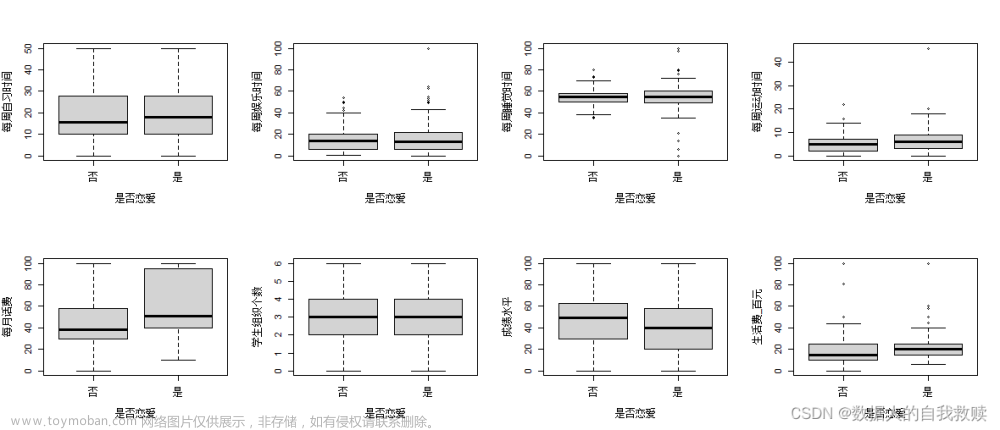
图3-11 箱线图
由图3-11可以得出:生活规划的变量在是否恋爱上不全存在差异性,从箱线图可以看出,每月话费、成绩水平和生活费在是否恋爱上存在较大的差异性,其它的变量差异性较小或几乎不存在差异性。
四、数据建模
4.1 全模型
(1)模型建立
将所有变量全部纳入模型,建立logistic回归模型,模型形式如下:
logitp=ln(p/1p)=β0+β1as.factorJB12+β2as.factorJB13+β3as.factorJB14+β4JB2+β5as.factorJB32+β6as.factorJB33+β7as.factorJB34+β8as.factorJB35+β9JB4+β10JB5+β11LA1+β12LA2+β13LA3+β14ZW1+β15ZW2+β16YD1+β17YD2+β18YD3+β19YD4+β20YD5+β21YD6+β22CY1+β23CY2+β24CY3+β25CY4+β26CY5+β27YZ1+β28YZ2+β29GH1+β30GH2+β31GH3+β32GH4+β33GH5+β34GH6+β35GH7+β36GH8
模型的参数估计如表4-1所示。
表4-1 全模型参数估计
| 变量 |
Estimate |
Pr(>|z|) |
变量 |
Estimate |
Pr(>|z|) |
| (Intercept) |
-4.4842 |
0.4128 |
YD4 |
-0.3917 |
0.3192 |
| as.factor(JB1)2 |
-0.5786 |
0.3699 |
YD5 |
0.1803 |
0.6461 |
| as.factor(JB1)3 |
0.2452 |
0.7283 |
YD6 |
1.1374 |
0.01987* |
| as.factor(JB1)4 |
-0.0625 |
0.9178 |
CY1 |
0.1752 |
0.6890 |
| JB2 |
0.3651 |
0.5629 |
CY2 |
1.1006 |
0.1791 |
| as.factor(JB3)2 |
0.0259 |
0.9702 |
CY3 |
-0.7648 |
0.2619 |
| as.factor(JB3)3 |
-0.5337 |
0.4534 |
CY4 |
0.4320 |
0.3584 |
| as.factor(JB3)4 |
-0.2499 |
0.7645 |
CY5 |
0.7619 |
0.1108 |
| as.factor(JB3)5 |
-1.2400 |
0.1846 |
YZ1 |
0.2786 |
0.4953 |
| JB4 |
0.0056 |
0.8628 |
YZ2 |
0.1027 |
0.2201 |
| JB5 |
-0.0015 |
0.9501 |
GH1 |
0.0033 |
0.8182 |
| LA1 |
2.0757 |
2.74e-06*** |
GH2 |
0.0085 |
0.6225 |
| LA2 |
2.1950 |
1.76e-07*** |
GH3 |
0.0070 |
0.7362 |
| LA3 |
1.5127 |
0.00234** |
GH4 |
0.0017 |
0.9685 |
| ZW1 |
-0.5238 |
0.2207 |
GH5 |
0.0136 |
0.08147· |
| ZW2 |
-0.0978 |
0.8492 |
GH6 |
0.1609 |
0.1713 |
| YD1 |
-0.3616 |
0.5976 |
GH7 |
-0.0122 |
0.1121 |
| YD2 |
-0.0400 |
0.9415 |
GH8 |
-0.0066 |
0.4049 |
| YD3 |
-0.9684 |
0.03585* |
由表4-1可以得出:
- 并不是所有的变量都在统计学意义上显著,其中变量LA1、LA2、LA3、YD3和YD6在统计学意义上显著,即变量是否追求过别人、是否被别人追求过、寝室同学是否谈过恋爱、乒乓球、台球在统计学意义上显著,其他自变量不显著。
- 追求过别人,学生恋爱的优势变为原来的7.97倍;被别人追求过,学生恋爱的优势变为原来的8.98倍;寝室同学谈过恋爱,学生恋爱的优势变为原来的4.54倍;打乒乓球,学生恋爱的优势变为原来的0.38倍,即学生恋爱发生的可能性降低;打台球,学生恋爱的优势变为原来的3.12倍。这些变化都在统计学意义上显著。
- 与大一学生相比,大二和大四学生恋爱的优势是大一学生的0.56倍和0.94倍,大三学生恋爱的优势是大一学生的1.28倍,即四个年级中,大三学生更可能谈恋爱,其次是大一学生、大四学生,最不可能谈恋爱的是大二学生,这些在统计学上不具有显著性。
- 与男学生相比,女学生恋爱的有时比是男同学的1.44倍,但这在统计学上不具有显著性。
- 与一线城市相比,二线城市学生恋爱的优势是其1.03倍,三线城市、县级市和农村学生恋爱的优势是其0.59倍、0.78倍和0.29倍,即二线城市学生最容易恋爱,其次是一线城市、县级市和三线城市,最后是农村学生。但是这些在统计学上不显著。
- 在其他条件不变的条件下,身高每增加1cm,学生恋爱的优势变为未增加时的1.0056倍;体重每增加1kg,学生恋爱的优势变为未增加前的0.99倍。但这些在统计学上不显著。
- 班干部、党员、踢足球、篮球、打羽毛球的学生恋爱的优势要低于非这些的学生,但是在统计学上不显著。
- 跑步、会唱歌、主持、乐器和其他才艺的学生恋爱的优势要高于非这些的学生,但在统计学上不显著。
- 学生的生活规划变量均对学生恋爱的优势比有正向影响,但这些影响在统计学上不存在显著性。
(2)结果预测
用全模型对第一个受访者的恋爱概率进行预测,预测值为-0.46617305,则恋爱的概率为p(Y=1) = 0.385522。当分界点α=0.5 时,第一个受访者被判为不恋爱,当分界点α=0.3 时,第一个受访者被判为恋爱。第一个受访者本身是不恋爱,因而α=0.5 时判断正确,α=0.3 时判断错误。
4.2 基于AIC准则下的选模型A
基于AIC准则对全模型的变量进行选择,得到选模型A,模型参数估计值如表4-2所示。
表4-2 选模型A参数估计结果
| 变量 |
Estimate |
Std.Error |
z value |
Pr(>|z|) |
| (Intercept) |
-1.9104 |
0.5541 |
-3.4480 |
0.0006*** |
| LA1 |
1.8057 |
0.3593 |
5.0250 |
5.03e-07*** |
| LA2 |
2.1443 |
0.3574 |
5.9990 |
1.98e-09*** |
| LA3 |
1.2134 |
0.4250 |
2.8550 |
0.0043* |
| YD3 |
-0.8502 |
0.4013 |
-2.1190 |
0.0341* |
| YD6 |
0.9293 |
0.4378 |
2.1230 |
0.0338* |
| GH5 |
0.0139 |
0.0062 |
2.2380 |
0.0252* |
| GH7 |
-0.0098 |
0.0063 |
-1.5590 |
0.1189 |
由表4-2可以得出:选模型A保留了变量LA1、LA2、LA3、YD3、YD6、GH5和GH7,即保留了是否追求过别人、是否被别人追求过、寝室同学是否谈过恋爱、乒乓球、台球、每月话费和成绩水平。除了变量成绩水平,其他变量在显著性水平α=0.05 下都具有统计学显著性。
4.3 基于BIC准则下的选模型B
基于BIC准则对全模型的变量进行选择,得到选模型B,模型参数估计值如表4-3所示。
表4-3 选模型B参数估计结果
| 变量 |
Estimate |
Std.Error |
z value |
Pr(>|z|) |
| (Intercept) |
-2.4436 |
0.4708 |
-5.1910 |
2.10e-07*** |
| LA1 |
1.7478 |
0.3423 |
5.1060 |
3.28e-07*** |
| LA2 |
2.0938 |
0.3418 |
6.1260 |
9.02e-10*** |
| LA3 |
1.3098 |
0.4128 |
3.1730 |
0.00151** |
| GH5 |
0.0165 |
0.0060 |
2.7440 |
0.00607** |
由表4-3可以得出:选模型B保留了变量LA1、LA2、LA3和GH5四个特别显著的变量,即保留了是否追求过别人、是否被别人追求过、寝室同学是否谈过恋爱和每月话费。这些变量在显著性水平α=0.05 下都具有较高显著性。
4.4 模型评估
以70%的样本作为训练集,30%样本作为测试集,通过ROC曲线比较全模型和选模型A、B的分类效果,得到的三个模型的ROC曲线如图4-1所示。同时,进行随机模拟,绘制三个模型外样本AUC箱线图如图4-2所示。
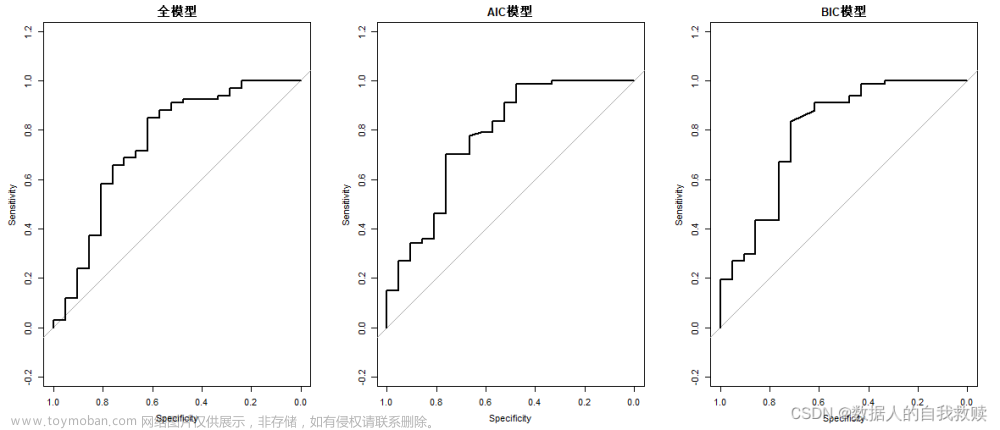
图4-1 三个模型的ROC曲线
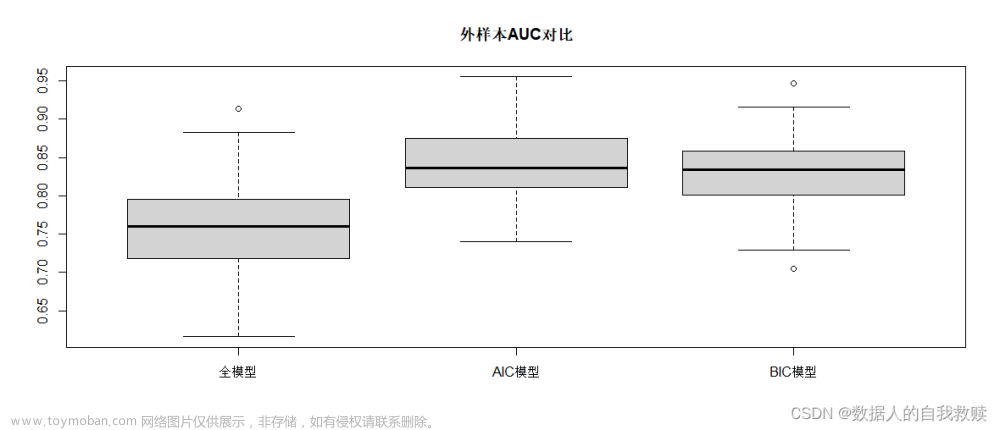
图4-2 三个模型AUC对比
结合图4-1和图4-2可以得出:AIC模型的ROC曲线与x轴围成的面积最大,且AIC模型AUC值的箱线图最高,综合ROC曲线和AUC值可以得出,三个模型中AIC模型分类效果最好。
五、结论及建议
5.1 结论
- 被调查的学生中,大四学生最多,男女比例基本一致,大部分学生来自于二三线城市,身高介于155-185cm之间,体重介于40-70kg之间,69.3%的人戴眼镜。
- 被调查学生中,72%的人恋爱,大部分人被别人追求过且为党员,且会跑步、打羽毛球、吹乐器和唱歌。
- 用全模型对第一个受访者的恋爱概率进行预测时,当分界点α=0.5 时,第一个受访者被判为不恋爱,当分界点α=0.3 时,第一个受访者被判为恋爱。第一个受访者本身是不恋爱,因而α=0.5 时判断正确,α=0.3 时判断错误。
- 是否追求过别人、是否被别人追求过、寝室同学是否谈过恋爱和每月话费对是否恋爱由显著影响。
- 结合ROC曲线和AUC值可以得出,三个模型中AIC模型分类效果最好。
5.2 建议
自身是否被追求过、是否追求过别人、寝室同学是否谈过恋爱和每月话费对大学生是否恋爱有显著影响。从中可以看出环境和自身意愿对是否恋爱的影响,要是想提升大学生恋爱意愿,可以加大宣传,以提升学生恋爱意愿。
六、代码
a=read.csv("D:/个人成长/学业/课程/大三下课程/统计模型/作业/第三次作业/大学生恋爱数据.csv",header=T)##读入文件
a[c(1:5),]
attach(a)
b=a[,22:32]
JB1=as.factor(JB1)
JB3=as.factor(JB3)
#统计恋爱状况
x=c(82,211)
color=c('red','orange')
piepercent1=round(100*x/sum(x),1)
pie(x,labels=piepercent1,main="是否恋爱",col=color)
legend("topright",c("否","是"),cex=0.8,fill=color)
#学生基本情况统计——年级、性别、家乡、身高、体重
x1=c(42,51,57,143)#年级
piepercent2=round(100*x1/sum(x1),1)
x2=c(144,149)#性别
piepercent3=round(100*x2/sum(x2),1)
x3=c(34,113,82,42,22)#家乡
piepercent4=round(100*x3/sum(x3),1)
par(mfrow=c(1,3))
pie(x1,labels=piepercent2,main="年级",col=rainbow(length(x1)))
legend("topright",c("大一","大二","大三","大四"),cex=1.5,fill=rainbow(length(x1)))
pie(x2,labels=piepercent3,main="性别",col=color)
legend("topright",c("男","女"),cex=1.5,fill=color)
pie(x3,labels=piepercent4,main="家乡",col=rainbow(length(x3)))
legend("topright",c("一线城市","二线城市","三线城市","县级市","农村"),cex=1.5,fill=rainbow(length(x3)))
#学生身高体重统计
par(mfrow=c(1,2))
hist(a$身高,main="身高",xlab="组别" ,ylab = "频数")#直方图
hist(a$体重,main="体重",xlab="组别" ,ylab = "频数")#直方图
#学生恋爱史统计
y1=c(134,159)#是否追求过别人
piepercent11=round(100*y1/sum(y1),1)
y2=c(75,218)#是否被别人追求过
piepercent12=round(100*y2/sum(y2),1)
y3=c(205,88)#寝室同学是否谈过恋爱
piepercent13=round(100*y3/sum(y3),1)
par(mfrow=c(1,3))
pie(y1,labels=piepercent11,main="是否追求过别人",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(y2,labels=piepercent12,main="是否被别人追求过",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(y3,labels=piepercent13,main="寝室同学是否谈过恋爱",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
#学生职务担任情况
z1=c(101,192)#班干部
piepercent21=round(100*z1/sum(z1),1)
z2=c(239,54)#党员
piepercent22=round(100*z2/sum(z2),1)
par(mfrow=c(1,2))
pie(z1,labels=piepercent21,main="班干部",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(z2,labels=piepercent22,main="党员",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
#学生运动情况
w1=c(257,36)#足球
piepercent31=round(100*w1/sum(w1),1)
w2=c(227,66)#篮球
piepercent32=round(100*w2/sum(w2),1)
w3=c(229,64)#乒乓球
piepercent33=round(100*w3/sum(w3),1)
w4=c(168,125)#羽毛球
piepercent34=round(100*w4/sum(w4),1)
w5=c(144,149)#跑步
piepercent35=round(100*w5/sum(w5),1)
w6=c(220,73)#台球
piepercent36=round(100*w6/sum(w6),1)
par(mfrow=c(2,3))
pie(w1,labels=piepercent31,main="足球",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(w2,labels=piepercent32,main="篮球",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(w3,labels=piepercent33,main="乒乓球",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(w4,labels=piepercent34,main="羽毛球",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(w5,labels=piepercent35,main="跑步",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(w6,labels=piepercent36,main="台球",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
#学生才艺情况
v1=c(195,98)#唱歌
piepercent41=round(100*v1/sum(v1),1)
v2=c(270,23)#主持
piepercent42=round(100*v2/sum(v2),1)
v3=c(268,25)#舞蹈
piepercent43=round(100*v3/sum(v3),1)
v4=c(180,110)#乐器
piepercent44=round(100*v4/sum(v4),1)
v5=c(133,160)#其他才艺
piepercent45=round(100*v5/sum(v5),1)
par(mfrow=c(2,3))
pie(v1,labels=piepercent41,main="唱歌",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(v2,labels=piepercent42,main="主持",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(v3,labels=piepercent43,main="舞蹈",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(v4,labels=piepercent44,main="乐器",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(v5,labels=piepercent45,main="其他才艺",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
#学生颜值情况
t1=c(90,203)#是否戴眼镜
piepercent51=round(100*t1/sum(t1),1)
par(mfrow=c(1,2))
pie(t1,labels=piepercent51,main="是否戴眼镜",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
hist(a$颜值,main="颜值",xlab="组别" ,ylab = "频数")#直方图
#学生生活规划情况
par(mfrow=c(2,4))
hist(a$每周自习时间,main="每周自习时间",xlab="组别" ,ylab = "频数")
hist(a$每周娱乐时间,main="每周娱乐时间",xlab="组别" ,ylab = "频数")
hist(a$每周睡觉时间,main="每周睡觉时间",xlab="组别" ,ylab = "频数")
hist(a$每周运动时间,main="每周运动时间",xlab="组别" ,ylab = "频数")
hist(a$每月话费,main="每月话费",xlab="组别" ,ylab = "频数")
hist(a$学生组织个数,main="学生组织个数",xlab="组别" ,ylab = "频数")
hist(a$成绩水平,main="成绩水平",xlab="组别" ,ylab = "频数")
hist(a$生活费_百元,main="生活费_百元",xlab="组别" ,ylab = "频数")
#连续变量之间相关性热力图
library(corrplot)
k=cor(b,use='everything',method='pearson')
par(mfrow=c(1,1))
corrplot(k,addCoef.col = "black")
#绘制箱线图
par(mfrow=c(2,4))
boxplot(a$每周自习时间~a$是否恋爱,ylab="每周自习时间",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$每周娱乐时间~a$是否恋爱,ylab="每周娱乐时间",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$每周睡觉时间~a$是否恋爱,ylab="每周睡觉时间",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$每周运动时间~a$是否恋爱,ylab="每周运动时间",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$每月话费~a$是否恋爱,ylab="每月话费",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$学生组织个数~a$是否恋爱,ylab="学生组织个数",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$成绩水平~a$是否恋爱,ylab="成绩水平",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$生活费_百元~a$是否恋爱,ylab="生活费_百元",xlab="是否恋爱",data=a,names=c("否","是"))
#全模型
model.full=glm(Y~as.factor(JB1)+JB2+as.factor(JB3)+JB4+JB5+LA1+LA2+LA3+ZW1+ZW2+YD1+YD2+YD3+YD4+YD5+YD6+CY1+
CY2+CY3+CY4+CY5+YZ1+YZ2+GH1+GH2+GH3+GH4+GH5+GH6+GH7+GH8,family=binomial(link=logit),data=a)
#模型结果,不显著的变量也要解读,加上不具有统计学意义
summary(model.full)
#似然比卡方检验模型整体效果
1-pchisq(30.56,df=7)
pred=predict(model.full,a)
#基于AIC准则下变量的选择
c(AIC(model.full),BIC(model.full))
model.aic=step(model.full,trace = F)
summary(model.aic)
ss=length(a[,1])#样本量
#基于BIC准则下变量的选择
model.bic=step(model.full,trace = F,k=log(ss))
summary(model.bic)
#只留了特别显著的变量
library(pROC)
#多次模拟,去除随机误差的影响(了解即可)
nsimu=100#进行100次模拟
p=0.7#用作训练集的样本概率
ss0=round(ss*p)#训练集样本量
AUC=as.data.frame(matrix(0,nsimu,3))#100行,3列的零数据框
names(AUC)=c("全模型","AIC模型","BIC模型")
#开始模拟
for(i in 1:nsimu){
#打乱a样本顺序,随即编号并排序
aa=a[order(runif(ss)),]
#数据集aa的前70%作为训练集
A0=aa[c(1:ss0),]
#数据集aa的后30%作为测试集
A1=aa[-c(1:ss0),]
model.1=glm(Y~as.factor(JB1)+JB2+as.factor(JB3)+JB4+JB5+LA1+LA2+LA3+ZW1+ZW2+YD1+YD2+YD3+YD4+YD5+YD6+CY1+
CY2+CY3+CY4+CY5+YZ1+YZ2+GH1+GH2+GH3+GH4+GH5+GH6+GH7+GH8,family=binomial(link=logit),data=A0)
model.2=glm(Y~LA1+LA2+LA3+YD3+YD6+GH5+GH7,family=binomial(link=logit),data=A0)
model.3=glm(Y~LA1+LA2+LA3+GH5,family=binomial(link=logit),data=A0)
#测试集检验模型效果,计算预测值
pred.1=predict(model.1,A1)
pred.2=predict(model.2,A1)
pred.3=predict(model.3,A1)
#计算AUC值
y=A1$Y
auc.1=roc(y,pred.1)$auc
auc.2=roc(y,pred.2)$auc
auc.3=roc(y,pred.3)$auc
#将各个AUC值填充到零矩阵中
AUC[i,]=c(auc.1,auc.2,auc.3)
}
#绘制箱线图看三个模型的AUC分布情况,AUC越大,模型分类效果越好
par(mfrow=c(1,1))
boxplot(AUC,main="外样本AUC对比")
#利用最后一次模拟数据绘制三个模型的ROC曲线
#计算混淆矩阵
roc.1=roc(y,pred.1)
roc.2=roc(y,pred.2)
roc.3=roc(y,pred.3)
#绘制三条ROC曲线,比较效果
par(mfrow=c(1,3))
plot(roc.1,main="全模型")
plot(roc.2,main="AIC模型")
plot(roc.3,main="BIC模型")
个人反思:描述性统计饼图过小,可以直接用一个表格计算出百分比即可,不必画这么多饼图文章来源:https://www.toymoban.com/news/detail-491173.html
个人意见,还请各位读者批评指正!文章来源地址https://www.toymoban.com/news/detail-491173.html
到了这里,关于【统计模型】大学生恋爱数据分析报告的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!