区块链的系统探索之路：椭圆曲线之有限域

有一种有效的学习方法叫费曼学习法。它的做法是把你学到的东西系统性的讲述出来，如果别人通过你的描述也能理解其中内容，这说明你对所学知识有了一定程度的掌握。目前我正在系统性的研究区块链技术，因此想借助费曼学习法，把我掌握的信息系统性的输出，一来能帮助自己更好的理解消化知识，另一方面也希望能帮助对这方面有兴趣的同学。当然区块链的技术信息汗牛充栋，相比与其他资料，我觉得我的优势在于能体会初学者的难处，因为我自己就是初学者。

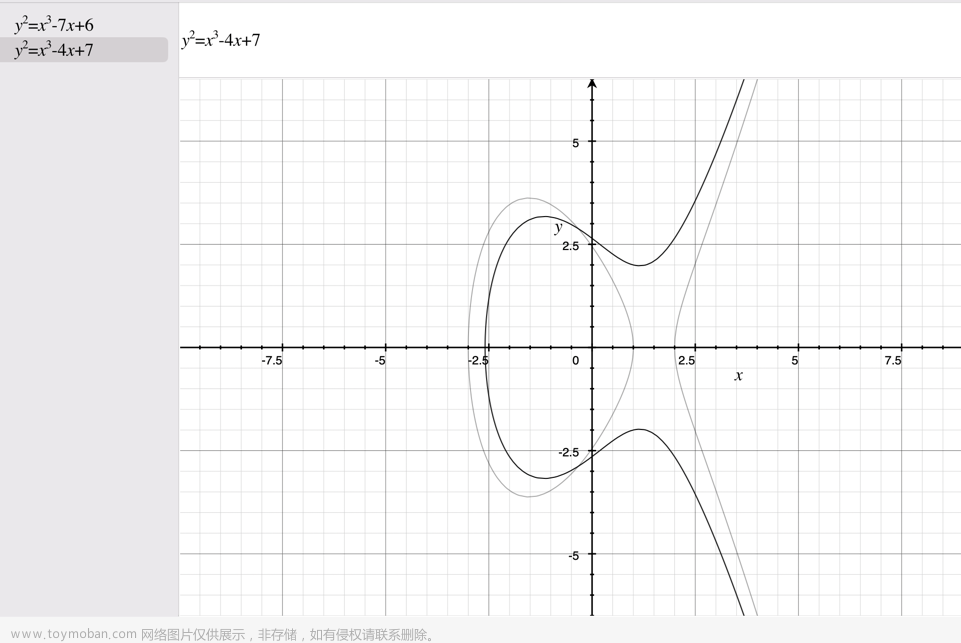
在我看来区块链技术的两大基础在于加解密和分布式。因此系统性的掌握区块链就需要系统性的掌握这两块。首先我们从加解密这块入手，其中这块中最基础的就是椭圆曲线。

从上面图形可以看到，椭圆曲线其实就是一个最高指数为3的多项式，这里需要注意的是多项式的计算要基于除法求余的基础，也就是它的计算方式如下：

y ^ 2 mod p = x^3 + a*x + b mod p

对于区块链而言他需要专门指定公式中a, b ， p 这个几个参数。因此它也有一个专有名字叫secp256k1，我们看看几个参数的具体数值：

p = 2 ^ 256 - 2 ^32 - 2 ^ 9 - 2 ^ 8 - 2 ^ 7 - 2 ^ 6 - 2 ^ 4 - 1
a = 0
b = 7

在运用中，x只取整数，我们使用代码看看椭圆曲线的例子;

def is_on_blockchain_curve(point):
    '''
    p = 2 ^ 256 - 2 ^32 - 2 ^ 9 - 2 ^ 8 - 2 ^ 7 - 2 ^ 6 - 2 ^ 4 - 1
    a = 0
    b = 7
    该函数判断给定的点是否在椭圆曲线上, 其中point包含两个数值(x,y)
    '''
    p = 2 ** 256 - 2 ** 32 - 2 ** 9 - 2 ** 8 - 2 ** 7 - 2 ** 6 - 2 ** 4 - 1
    return (point[1] ** 2) % p == (point[0] ** 3 + 7) % p

p = (55066263022277343669578718895168534326250603453777594175500187360389116729240,
     32670510020758816978083085130507043184471273380659243275938904335757337482424)

print(f"is point p on curve: {is_on_blockchain_curve(p)}")

上面代码构造了椭圆曲线，然后给定一个点p,并判断这个点是否在曲线上，代码运行后返回结果为:

is point p on curve: True

也就是给定的P点确实在曲线上，从这里可以看出，椭圆曲线在运用时，我们需要处理数值相当大的点。

在数学上椭圆曲线定义了一种运算叫"加法“，千万不要将其与我们普通的四则运算等同起来，我们看看椭圆曲线的"加法"是如何运作的。在椭圆曲线上取两点，如果这两点不是同一点，那么这两点相加的运算如下图所示:

P, Q是曲线上两点，P + Q的结果就是，先将P,Q两点连线，这条线会跟曲线交在第三点也就是上方的R点，然后找这点相对x轴的对称点，那点的左边就是P+Q的结果。如果P,Q指的是同一点，那么就在这点上做曲线的切线，这条切线会跟曲线交于第二点，把交点根据x轴进行对称操作，所得的点就是加法的结果，如下图所示：

对于椭圆曲线上针对某个点做乘法，实际上就是将加法重复相应的次数。椭圆曲线在区块链上的一大应用就是创建个人钱包的地址，这个地址类似于TCP/IP协议上的IP地址，通过这个地址，别人就可以跟你交换数据，例如将比特币转移给你。要想创建个人钱包地址，我们需要先从椭圆曲线创建一个叫"公钥”的数据，首先我们在曲线上取专门的一点用G表示，然后创建一个足够大的随机数k,然后计算这两个数相乘的结果 K = k * G , 注意这里G是椭圆曲线上的一个点，k是一个很大的整数，乘法操作就是把上面描述的加法重复k次，在这里k就是区块链用户的私钥，K就是公钥，在数学上可以证明，通过K是不能计算出k的，因此我们可以将K发布到网络上作为个人的地址。

我们看4 * G的计算过程:

首先我们计算2*G,那就是在G点做切线，它跟曲线的另一个交点记作-2G，然后根据x轴做对称得到点2G,然后对点2G做切线，它与曲线相交于点-4G,然后再根据x轴做对称得到最终结果4G，在上图中G点是一个事先指定好在椭圆曲线上的一个点，它的坐标为(0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)，可以看到这是一个相当巨大的天文数字，下面我们从数学原理并结合代码的方式来深入认识一下椭圆曲线的原理。

几乎所有加解密的原理都基于抽象代数。特别是在抽象代数中的有限域这个概念。所谓有限域它是一个包含有限个元素的集合，同时它支持两种运算，分别用“+”和“*”，来表示，这两种运算具有如下性质：
1，如果a, b 是集合中两个元素，那么a + b 和 a * b 所的的结果也属于该集合，这个性质叫闭合性。
2，集合中存在一个特殊元素用符号0表示，它满足0 + a = a
3，集合中存在一个特殊元素，用1表示，它满足 1 * a = a
4, 对集合中任何一个元素a, 集合还存在另一个对应元素记作-a, 它满足a + (-a) = 0
5, 对集合中任何一个元素a, 集合还存在另一个对应元素记作a^(-1)，它满足 a * a^(-1) = 1

这里我们需要注意，千万不要把操作+和* 跟四则运算中的加法和乘法等同起来，由于整数或实数中对应的加法和乘法都满足上面性质，因此我们在思维上会不自觉把上面定义的两种操作等同起来，因此一定要注意不要等同，不然它会对我们的理解造成很大的障碍。

有几个要点需要注意，首先集合里面元素的个数必须是有限的，假设集合中包含元素的个数为p,那么我们把p称作该集合的order。对于第一点要求，我们必须确保+和*两种操作是闭合的，假设集合元素为{1,2,3}，这两种操作对应四则运算的加法和乘法，那么这两种操作就不能实现闭合，因为1+3等于4，而4不在集合中。但是对于集合{1, 0, -1},那么四则元素的加法和乘法对于这个集合的元素就是闭合的。所以我们不要把普通的加法和乘法跟上面的定义等同起来。同时需要注意的是，对有限域而言，它元素的个数需要是素数。为了更好的理解有限域，我们看看如何使用python来实现。

class LimitFieldElement: #实现有限域的元素
    def __init__(self, num, order):
        """
        order 表示集合元素的个数，它必须是一个素数，不然有限域的性质不能满足
        num 对应元素的数值
        """

        if order <= num < 0:
            err = f"元素 {num} 数值必须在0到 {order - 1} 之间"
            raise ValueError(err)
        self.order = order
        self.num = num

    def __repr__(self):
        return f"LimitFieldElement_{self.order}({self.num})"

    def __eq__(self, other):
        if other is None:
            return False
        return self.num == other.num and self.order == other.order
        
    def __ne__(self, other):
        if other is None:
            return True

        return self.num != other.num or self.order != other.order
       

上面代码首先定义有限域元素，同时规定元素对应的值必须在0到集合元素个数之间，同时要注意，集合元素的个数需要是素数，不然它对应的性质就会有问题。注意到前面描述有限域中元素有两种运算，分别是"+“, 和”*"，这两种运算的特性是具有闭合性，也就是说两个元素执行这两种运算后，所得结果依然属于该集合，前面我们也看到，我们熟悉的四则元素加法和乘法不一定能满足闭合性，但是我们稍微对这两种运算做一个简单的“加工”，就能满足，这个“加工”就是基于求余的加法和乘法，具体来说就是对两个元素进行四则运算的加法和减法后，再把所得结果根据集合元素的个数进行求余。

举个具体例子，对应集合{0, 1, 2, 3, 4} ，3“+”5的过程为先计算3加上5的结果，也就是8，然后对对集合元素个数做求余，由于集合元素有5个，因此3 = 8 % 5 , 于是3 “+” 5的结果就是3.虽然在集合中所有元素都是正数，但是我们可以在运算”+“的基础上定义负数，如果集合中两个元素a,b，执行操作a “+” b 后结果为0， 那么我们就规定 b 可以记作-a。

这里有点违法我们的直觉，因为根据上面的定义对于元素2, 那么-2 其实就是元素3， 因为2 “+” 3 = 0，初次接触到有限域运算的同学可能会比较迷糊。下面我们把操作“+”实现在有限域的元素上，对应代码如下：

    def __add__(self, other):
        """
        有限域元素的"+"操作，它是在普通加法操作的基础上，将结果对集合中元素个数求余
        """
        if self.order != other.order:
            raise TypeError("不能对两个不同有限域集合的元素执行+操作")
        #先做普通加法，然后在结果基础上相对于集合元素的个数做求余运算
        num = (self.num + other.num) % self.order
        """
        这里使用__class__而不是LimitFieldElemet是为了后面实现类的继承考虑，
        后面我们实现的对象需要继承与这个类
        """
        return self.__class__(num, self.order)

实现上面的方法后，下面的代码结果为True:

a = LimitFieldElement(7, 13)
b = LimitFieldElement(12, 13)
c = LimitFieldElement(6, 13)
print(a + b == c)

完成了"+“操作下面我们看看”*“操作，跟”+“操作一样，”*“操作就是先将两个元素进行普通乘法操作，然后将结果针对集合的元素个数执行求余操作，例如对于集合{0, 1, 2, 3, 4}, 对于3 “*” 4, 我们先计算3*4 = 12，然后对集合元素个数求余，也就是12 % 5 = 2, 于是 3 “*” 4 = 2，在”*“操作的基础上我们可以定义倒数这个概念，对于元素a,b，如果a “*” b = 1，那么我们就规定b 可以记作1/a, 或者a 可以记作1/b。在”*"操作的基础上，我们还可以定义指数操作，对于集合中的元素a, a ^ 3对应的是a “*” a “*” a,我们看看对应操作的代码实现，相关代码如下:

 def __mul__(self, other):
        """
        有限域元素进行"*"操作时，先执行普通的乘法操作，然后将结果针对集合元素的个数进行求余
        """
        if self.order != other.order:
            raise TypeError("能对两个不同有限域集合的元素执行*操作")
        
        num = (self.num * other.num) % self.order
        return self.__class__(num, self.order)
    
    def __pow__(self, power, modulo=None):
        """
        指数操作是先执行普通四则运算下的指数操作，再将所得结果针对集合元素个数求余
        """
        num = (self.num ** power) % self.order
        return self.__class__(num, self.order)

完成上面两个函数后，如下代码在执行时返回结果都是True:

a = LimitFieldElement(3, 13)
b = LimitFieldElement(12, 13)
c = LimitFieldElement(10, 13)
print(a * b == c)

a = LimitFieldElement(3, 13)
b = LimitFieldElement(1, 13)
print(a ** 3 == b)

相对于“+”的逆运算我们定义为“-”，它的运算比较简单，对于两个集合中的元素a,b，计算a"-“b，我们先用四则运算中的减法获得其结果，然后再将结果对应到集合中的元素，例如集合{0, 1, 2 ,3 ,4}，a = 1, b = 3, 那么a “-” b就先对其进行正常的减法运算，然后将结果针对元素个数求余，因此 1 “-” 3 就先计算 1 - 3 = -2， 然后再对元素个数也就是5求余，-2 % 5 = 3，也就是1 “-” 3 = 3，如此看起来是有点反直觉。下面我们看看”*"操作下，所定义除法操作的实现，这里我们就需要一点数学推导了，以下将是一个理解难点。

对于操作“/"而言，我们不能像前面那样，先做普通的除法然后再将结果针对集合元素个数求余。这里我们需要使用一个名为费马小定理，它的内容如下：

对任一素数p，以及任意正整数n，n % p != 0，那么有：n^(p-1) % p = 1
(这里的运算对应普通的四则运算)

这个定理有很多证明方法，一种简单的做法是，如果p是素数，然后给定任意一个整数n > 0, 我们有{1, …, p - 1} 等同于({n% p, 2n%p, … (p-1)n%p}，需要注意的是，这里的等同是指两个集合包含相同的元素，而不是指两个集合的元素一一对应。我们简单研究一下这个结论，由于在第二个集合中，每个元素都对应形式( k * n) % p, 1 <= k <= p-1,由于对p求余，因此第二个集合最多包含p - 1个元素，而且元素值不超过p，如果第二个集合中没有重复元素，那么集合就包含p-1元素，由此两个集合就包含相同元素，于是两个集合等价。

假设第二个集合包含重复元素，那意味着存在1 <= t, k <= p-1, t !=k, 但是有 (t*n) % p = (k * n) % p，不失一般性，假设t > k， 那么有 [(t * n) - (k * n)] % p = 0，合并一下就有[(t - k) * n] % p = 0，由于我们在定理说明中已经有 n % p != 0,因此这个等式要成立就必须有(t-k) % p = 0, 但是我们已经知道 1 <= t < k < p - 1, 因此t - k < p, 由此(t - k) % p不能等于0，有就是说第二个集合中没有重复元素，于是两个集合包含相同元素。

于是我们就有 [1 * 2 * … * (p-1)] % p = [ (n%p) * (2n) % p * … * (p-1)*n]，简化一下两边就有(p-1)! % n = (p-1)!*(n^(p-1)) % n, 两边消掉(p-1)!%n就有 1 = n ^ (p-1) % n。

由于要计算 a “” b， 我们只要找到另一个元素c, 如果它满足 c “*” b = 1, 那么 a “” b 就转换为a “*” c，这时候费马小定理就能发挥作用，因为有b^(p-1) % p = 1, 由此我们得出c = [b ^ (p-2)] % p，由于我们已经知道如何做指数运算，因此就可以计算出c的值，由此就能计算 a “” b。

下面我们看看运算""的实现。在前面实现的函数__pow__中，我们其实可以使用python自带的pow函数来实现，这个函数不但能实现指数运算，而且还能实现基于求余的指数运算，它第三个参数就可以指定要求余的数值p，但是有个问题在于它不能接受负数，如果第二个参数是负数他就会抛出异常。因此我们不能执行pow(3, -5, 17)，但是由于有费马小定理，a ^ (p-1) % p = 1, 于是 a ^ (-5) % p = a ^ (-5) %p * a^(p-1) % p = a ^ (p-6) % p,于是我们就有pow(3, -5 , 17) = pow(3, 17-6 , 17),因此我们可以将我们前面对__pow__的实现优化如下：

    def __pow__(self, power, modulo=None):
        """
        指数操作是先执行普通四则运算下的指数操作，再将所得结果针对集合元素个数求余
        """
        while power < 0:
            power += self.order
        num = pow(self.num, power, self.order)
        return self.__class__(num, self.order)

最后我们基于上面的代码来实现"/"操作：

    def __truediv__(self, other):
        if self.order != other.order:
            raise TypeError("不能对两个不同有限域集合的元素执行*操作")
        #通过费马小定理找到除数的对应元素
        negative = other ** (self.order - 2)
        num = (self.num * negative.num) % self.order
        return self.__class__(num, self.order)

有了"/"运算后，下面的代码运行后输出结果为True:

a = LimitFieldElement(3, 13)
#由于(7 * 2) % 13 = 1，因此元素3 "/" 7 等价余 3 "*" 2, 因此 3 "/" 7 = 3 "*" 2 = 6
b = LimitFieldElement(7, 13)
c = LimitFieldElement(6, 13)

以上的内容就是区块链技术中对应的有限域原理以及实现，完整代码的下载地址：https://github.com/wycl16514/blockchain_finit_field.git，下一节我们看看椭圆曲线是如何在有限域的基础上实现数据加密的，更多内容请在b站搜索"Coding迪斯尼"。文章来源地址https://www.toymoban.com/news/detail-491207.html

到了这里，关于区块链的系统探索之路：椭圆曲线之有限域的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！