最短路问题 Bellman-Ford（单源最短路径）(图解)-Toy模板网

这篇具有很好参考价值的文章主要介绍了最短路问题 Bellman-Ford（单源最短路径）(图解)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

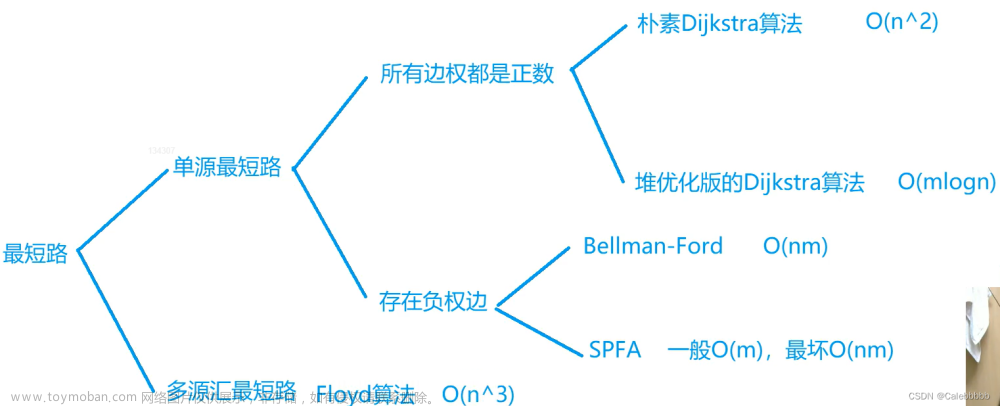
核心思想：松弛操作

对于边(u,v)，用dist（u）和（u，v）的和尝试更新dist（v）:

dist(v) = min(dist(v) , dist(u)+l(u,v)

注：dist（i）为源点（起点）到i点的距离，l（u，v）为u->v的边权。

Bellman-Ford的基本操作是进行多次迭代，每一轮迭代对图上所有边进行松弛操作，直到再一次迭代中没有点的dist发生变化即可停止迭代。为什么呢？不妨假设已经没有dist发生变化了，再进行一轮迭代的话，很显然，之后的迭代没有产生任何作用，dist数组依旧没有改变，反倒增大了时间复杂度，这不是多此一举么。

图解：

最短路问题 Bellman-Ford（单源最短路径）(图解)

初始：（S为源点）

初始设置为inf无穷大，表示还没有最短路

S	A	B	C	D	E
0	inf	inf	inf	inf	inf

第一轮迭代：

对S点连出的边（s->e，s->a）

S	A	B	C	D	E
0	7(0+7)	inf	inf	inf	5(0+5)

对A连出的边（a->c）

S	A	B	C	D	E
0	7	inf	9(7+2)	inf	5

对B连出的边（b->a)

S	A	B	C	D	E
0	7	inf	9	inf	5

dist(B)还没有找到最短路，更新其他点的最短路径无意义，故对B点的出边不进行松弛

对C连出的边（c->b）

S	A	B	C	D	E
0	7	7(9+(-2))	9	inf	5

对D连出的边（d->c,d->a）

S	A	B	C	D	E
0	7	7	9	inf	5

dist(D)还没有找到最短路，更新其他点的最短路径无意义，故对D点的出边不进行松弛

对E连出的边（e->d）

S	A	B	C	D	E
0	7	7	9	6(5+1)	5

已经对所有的边进行了松弛操作，第一轮迭代结束

第二轮迭代

对S点连出的边（s->e，s->a）

S	A	B	C	D	E
0	7	7	9	6	5

无需更新

对A连出的边（a->c）

S	A	B	C	D	E
0	7	7	9	6	5

无需更新

对B连出的边（b->a)

S	A	B	C	D	E
0	7	7	9	6	5

无需更新

对C连出的边（c->b）

S	A	B	C	D	E
0	7	7	9	6	5

无需更新

对D连出的边（d->c,d->a）

S	A	B	C	D	E
0	2(6+(-4))	7	5(6+(-1))	6	5

对E连出的边（e->d）

S	A	B	C	D	E
0	2	7	5	6	5

已经对所有的边进行了松弛操作，第二轮迭代结束

第三轮迭代

与第一第二轮同理（此处直接给出迭代结束的结果）

S	A	B	C	D	E
0	2	2	4	6	5

第四轮迭代

无任何更新，迭代结束，更新完成

算法分析：

如果最短路存在，一定存在一个不含环的最短路。（理由：对零环和正环，去掉后路径不会变长；对负环，若最短路径中存在负环，那一定不是最短路，负环可以无限绕下去，路径可以是负无穷）

最短路不含环，那么一条最短路径最多经过n-1个点（不含起点），所以最多需要n-1轮松弛操作。

复杂度分析：

最多进行n-1次迭代，每次迭代枚举遍历所有边，尝试通过边进行松弛操作，故复杂度为

O(N-1)*O(M)即O(NM)，（注：N为点数，M为边数）

伪代码

for (int i = 0; i <= n; i++)

dist[i] = inf;//初始化为无穷大

dist[s] = 0;//s为起点，自己到自己的最短路为0

for (int k = 1; k <= n - 1; k++)//迭代n-1轮

{

for (int i = 1; i <= m; i++)//枚举每一条边

{

int x = u[i], y = v[i];

if (dist[x] < inf)

dist[y] = min(dist[y], dist[x] + w[i]);//松弛

}

}

检查有无负环

将dist数组初始化为0，迭代n-1次后进行第n次迭代，如果第n次迭代有进行松弛操作，则一定存在负环，因为不存在负环最多只能进行n-1次松弛操作

代码实现：

void bellman_ford(int s, int end) // s为起点,end为终点

{

memset(dis, 127, sizeof(dis));

dis[s] = 0; //起点最短路为0

pre[s] = -1;

for (int i = 1; i <= n - 1; i++)

{

bool ok = false;

for (int j = 1; j <= m; j++)

{

int x = edge[j].u, y = edge[j].v, w = edge[j].w;

if (dis[x] < (1 << 30) && dis[x] + w < dis[y])

{

dis[y] = dis[x] + w;

pre[y] = x; // y的上一个点为x，如不需打印路径无需pre数组

ok = true;

}

}

if (ok == false)

{

break; //未进行松弛操作，提前退出循环，减小时间复杂度

}

}

if (dis[end] < (1 << 30))

cout << dis[end] << "\n";

else

cout << "-1\n";

// Print_Path(end); //打印路径

}

模板题

题目链接：最短路 - 题目 - Daimayuan Online Judge

题目描述：

给你一张简单有向图，边权都为非负整数。以及一些询问，询问两个点之间的距离。

图用以下形式给出：

第一行输入三个整数 n,m,k表示图的顶点数、边数和询问次数，顶点编号从 1 到 n。

接下来 m 行，每行三个整数 x,y,z表示 x 到 y 有一条有向边，边权为 z。

接下来 k 行，每行两个整数 x,y 询问从 x 到 y 的最短路长度，如果无法到达，输出 −1。

输入格式：

第一行三个整数 n,m,k 表示图的顶点数、边数和询问次数。

接下来 m 行，每行有三个整数，代表一条边。

接下来 k 行，每行有两个整数，代表一次询问。

输出格式：

输出共 k 行，每行一个数表示一次询问的答案。

数据规模：

对于所有数据，保证 2≤n≤5000,0≤m≤10000,1≤k≤5,1≤x,y≤n,x≠y,1≤z≤10000。

样例输入：

3 3 2

1 2 3

2 3 2

3 2 1

1 3

3 1

样例输出：

5

-1

直接给代码了

#include <bits/stdc++.h>
using namespace std;
struct Edge
{
    int u, v, w;
} edge[100009];
int pre[100009];          //记录上一个点，为了打印最短路径
int dis[100009], n, m, k; // n为点数，m为边数，dis[i]为起点到i的最短距离
void Print_Path(int x)
{
    if (pre[x] == -1)
    {
        cout << x; //起点的pre为-1，所以x为起点
        return;
    }
    else
    {
        Print_Path(pre[x]);
        cout << "->" << x;
    }
}
void bellman_ford(int s, int end) // s为起点,end为终点
{
    memset(dis, 127, sizeof(dis));
    dis[s] = 0; //起点最短路为0
    pre[s] = -1;
    for (int i = 1; i <= n - 1; i++)
    {
        bool ok = false;
        for (int j = 1; j <= m; j++)
        {
            int x = edge[j].u, y = edge[j].v, w = edge[j].w;
            if (dis[x] < (1 << 30) && dis[x] + w < dis[y])
            {
                dis[y] = dis[x] + w;
                pre[y] = x; // y的上一个点为x
                ok = true;
            }
        }
        if (ok == false)
        {
            break; //未进行松弛操作，提前退出循环，减小时间复杂度
        }
    }
    if (dis[end] < (1 << 30))
        cout << dis[end] << "\n";
    else
        cout << "-1\n";
    // Print_Path(end); //打印路径
}
int main()
{
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr); //关同步流
    cin >> n >> m >> k;
    for (int i = 1; i <= m; i++) //读入边
    {
        cin >> edge[i].u >> edge[i].v >> edge[i].w;
    }
    for (int i = 1; i <= k; i++) // k次询问
    {
        int x, y;
        cin >> x >> y;
        bellman_ford(x, y);
    }
}

参考文献：

《算法竞赛，入门经典（第二版）》

2022 Namomo Spring Camp Div2 Day8 直播课

ending

有什么错误之处欢迎指正！不胜感激！文章来源地址https://www.toymoban.com/news/detail-491285.html

到了这里，关于最短路问题 Bellman-Ford（单源最短路径）(图解)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！