ID3决策树及Python实现（详细）

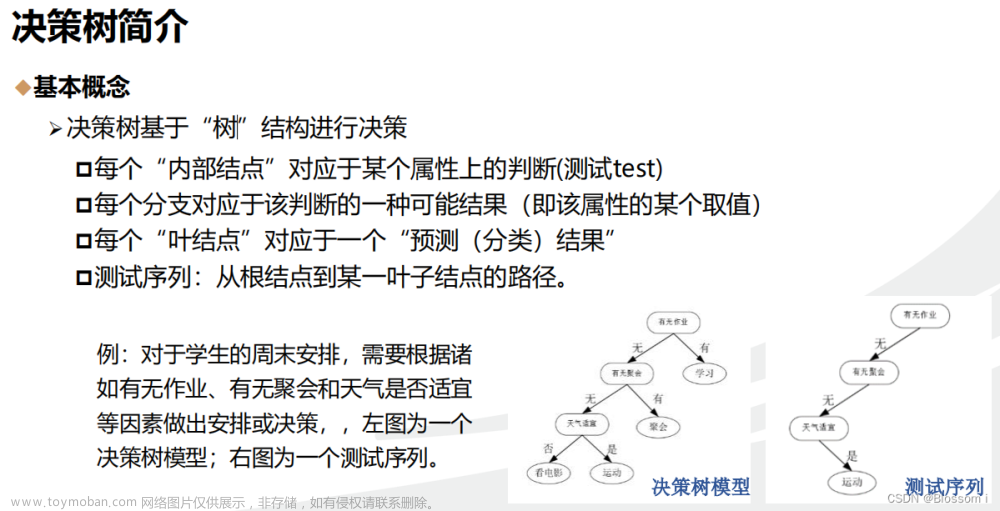
目录

一、划分特征的评价指标：

二、决策树学习算法伪代码：

三、决策树生成实例：

四、Python实现ID3决策树：

一、划分特征的评价指标：

1、信息熵 Ent(D)：

信息熵，是度量样本集合纯度的一种指标，Ent(D)的值越小，则样本集D的纯度越高；

2、信息增益 Gain(D,a)：

信息增益越大，则意味着使用属性a来划分所获得的“纯度提升”越大；ID3决策树算法就是基于信息增益来划分属性，下面介绍ID3决策树的构建过程；

公式中各变量说明：

D：样本集；

y：标签（比如好瓜、坏瓜）；

pk：某一类样本占总样本数的比例；

V：属性的取值（比如纹理属性有3种取值：清晰、稍糊、模糊）；

Dv：属性值==V从样本集D划分出的一个样本子集；

二、决策树学习算法伪代码：

决策树的生成是一个递归的过程，在决策树基本算法中，有三种情形会导致递归返回：

1. 当前结点包含的样本全属于同一类别，无需划分；
2. 当前属性集为空，或是所有样本在所有属性上取值相同，无法划分；
3. 当前结点包含的样本集合为空，不能划分； 

三、决策树生成实例：

3.1 首先获取一个训练样本集D，作为决策树的训练依据：

3.2 计算信息增益：

1、计算信息熵 Ent(D)：

2、计算当前特征集合 {色泽,根蒂,敲声,纹理,脐部,触感} 中各个特征a的信息增益Gain(D,a)：

 以“色泽”为例计算Gain(D,色泽)：

色泽的取值：{青绿,乌黑,浅白}，使用“色泽”特征对D划分可以得到3个子集：D1(色泽=青绿)={1,4,6,10,13,17}，D2(色泽=乌黑)={2,3,7,8,9,15}，D1(色泽=浅白)={5,11,12,14,16}，计算划分子集后分支结点的熵 ：

所以，得到Gain(D,色泽)：

 同理，计算其他特征的信息增益Gain(D,a)：

3.3 选取最优信息增益，选取最优划分特征：

因为Gain(D,纹理)最大，所以选取“纹理”作为本轮划分的最优划分特征，继而可以得到基于“纹理”的根节点划分：

3.4 决策树算法再对每个分支进一步划分（递归）：

将每个分支可以看成一个新的样本集，进行进一步的划分，在计算各特征信息增益时，需要将上一轮选出的最优特征在样本中去掉，不需要再对该特征进行比较。

就比如D1={1,2,3,4,5,6,8,10,15}，特征集合={色泽,根蒂,敲声,脐部,触感}。基于D1计算出各特征的信息增益Gain(D1,a)：

继续选取最大的特征信息增益，选出最优划分特征，即重复3.3步骤，递归实现决策树的建立；

3.5 生成最终的决策树：

四、Python实现ID3决策树：

总样本集：

['青绿','蜷缩','浊响','清晰','凹陷','硬滑','好瓜'],
['乌黑','蜷缩','沉闷','清晰','凹陷','硬滑','好瓜'],
['乌黑','蜷缩','浊响','清晰','凹陷','硬滑','好瓜'],
['青绿','蜷缩','沉闷','清晰','凹陷','硬滑','好瓜'],                
['青绿','稍蜷','浊响','清晰','稍凹','软粘','好瓜'],               
['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','好瓜'],                
['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','好瓜'],
['浅白','蜷缩','浊响','清晰','凹陷','硬滑','好瓜'],
['浅白','蜷缩','浊响','模糊','平坦','硬滑','坏瓜'],
             
['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','坏瓜'],
['青绿','硬挺','清脆','清晰','平坦','软粘','坏瓜'],
['浅白','蜷缩','浊响','模糊','平坦','软粘','坏瓜'],
['青绿','稍蜷','浊响','稍糊','凹陷','硬滑','坏瓜'],  
['浅白','稍蜷','沉闷','稍糊','凹陷','硬滑','坏瓜'],
['浅白','硬挺','清脆','模糊','平坦','硬滑','坏瓜'],
['乌黑','稍蜷','浊响','清晰','稍凹','软粘','坏瓜'],
['青绿','蜷缩','沉闷','稍糊','稍凹','硬滑','坏瓜']

下面从总样本种提取序号5、12、17为验证集，剩下为训练集进行训练决策树；

（1）训练集：

['青绿','蜷缩','浊响','清晰','凹陷','硬滑','好瓜'],
['乌黑','蜷缩','沉闷','清晰','凹陷','硬滑','好瓜'],
['乌黑','蜷缩','浊响','清晰','凹陷','硬滑','好瓜'],
['青绿','蜷缩','沉闷','清晰','凹陷','硬滑','好瓜'],
['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','好瓜'],
['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','好瓜'],
['浅白','蜷缩','浊响','清晰','凹陷','硬滑','好瓜'],

['浅白','蜷缩','浊响','模糊','平坦','硬滑','坏瓜'],
['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','坏瓜'],
['浅白','蜷缩','浊响','模糊','平坦','软粘','坏瓜'],
['青绿','稍蜷','浊响','稍糊','凹陷','硬滑','坏瓜'],
['浅白','稍蜷','沉闷','稍糊','凹陷','硬滑','坏瓜'],
['浅白','硬挺','清脆','模糊','平坦','硬滑','坏瓜'],
['青绿','蜷缩','沉闷','稍糊','稍凹','硬滑','坏瓜']

（2）验证集：

['青绿','稍蜷','浊响','清晰','稍凹','软粘'], ['好瓜']
['青绿','硬挺','清脆','清晰','平坦','软粘'], ['坏瓜']
['乌黑','稍蜷','浊响','清晰','稍凹','软粘'], ['坏瓜']

下面编写各个函数，每个函数有特定的功能，代码的分析过程已在code后注释。

4.1 构建样本集：

#? 构建数据集
#  返回一个元组 (dataSet,labels)
def createDataSet():    # 创造示例数据
    dataSet=[['青绿','蜷缩','浊响','清晰','凹陷','硬滑','好瓜'],
             ['乌黑','蜷缩','沉闷','清晰','凹陷','硬滑','好瓜'],
             ['乌黑','蜷缩','浊响','清晰','凹陷','硬滑','好瓜'],
             ['青绿','蜷缩','沉闷','清晰','凹陷','硬滑','好瓜'],                
             ['青绿','稍蜷','浊响','清晰','稍凹','软粘','好瓜'],               
             ['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','好瓜'],                
             ['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','好瓜'],
             
             ['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','坏瓜'],
             ['青绿','硬挺','清脆','清晰','平坦','软粘','坏瓜'],
             ['浅白','蜷缩','浊响','模糊','平坦','软粘','坏瓜'],
             ['青绿','稍蜷','浊响','稍糊','凹陷','硬滑','坏瓜'],  
             ['浅白','稍蜷','沉闷','稍糊','凹陷','硬滑','坏瓜'],
             ['乌黑','稍蜷','浊响','清晰','稍凹','软粘','坏瓜'],
             ['青绿','蜷缩','沉闷','稍糊','稍凹','硬滑','坏瓜']]
    labels = ['色泽','根蒂','敲声','纹理','脐部','触感']  #六个特征
    return dataSet,labels

函数作用：用于构建训练集

变量说明：

1. dataSet：样本集
2. labels：所有特征

4.2 计算信息熵：

#? 计算信息熵
#  返回输入样本集dataSet的信息熵 Ent
from math import log
def calEnt(dataSet):
    sampleCounts=len(dataSet)   # 样本集的样本数
    labelCounts={}              # key为标签值label（好瓜、坏瓜），value为对应标签key在样本集中出现的次数
    for sample in dataSet:      # 遍历样本集dataSet中每个样本sample
        label=sample[-1]        # 标签label为样本sample的最后一个元素值
        if label not in labelCounts.keys():     # 如果该标签label不在字典labelCounts的key值中
            labelCounts[label]=0                # 则新增该key，并赋初值0
        labelCounts[label]+=1   # 对遍历到的每个sample统计其所属标签的个数
    Ent=0.0     # 信息熵初始化
    for key in labelCounts:
        pro=float(labelCounts[key])/sampleCounts    # 具体标签占总样本数的比例pro
        Ent-=pro*log(pro,2)     # 计算样本集dataSet的信息熵Ent
    return Ent

函数作用：计算样本集dataSet的信息熵E(dataSet)

变量说明：

1. dataSet：传入的样本集
2. sampleCounts：样本集中的样本数
3. labelCounts：key为标签值（好瓜/坏瓜），value为对应标签key在样本集中出现的次数
4. sample：具体样本
5. label：标签（好瓜、坏瓜）
6. pro：具体标签占总样本数的比例
7. Ent：样本集dataSet的熵 Ent(D)

4.3 按给定的特征值划分出样本子集：

#? 按给定特征值划分出样本子集
#  指定特征列的索引index，对特征值==value的样本划分出来为一个样本子集retDataSet，并对这些样本的value去掉，返回样本子集 retDataSet
def splitDataSet(dataSet,index,value):      # index是指定特征列的索引，value是该特征下的某一特征值
    retDataSet=[]
    for sample in dataSet:                  # 遍历样本集dataSet中的具体样本sample
        if sample[index]==value:            # 找到目标特征值value的索引
            # 去除特征值==value这些样本的vlaue值
            reducedSample=sample[:index]            # 剪下目标索引前的列表
            reducedSample.extend(sample[index+1:])  # 将目标索引后的列表添加到索引前列表的后面
            retDataSet.append(reducedSample)        # 将sample[index]==value并去除该vlaue的样本添加到retDataSet样本集中
    return retDataSet

函数作用：指定特征列的索引index，对样本集中特征值==value的具体样本sample划分出来，组成一个dataSet的样本子集retDataSet（并将这些样本中的这些value去掉，去掉sample[index]的目的是因为下轮比较各特征信息增益Gain从而获得最大信息增益bestGain（决定最优划分特征bestFeature）时，不能将已选出的最优特征放在比较队列中）

变量说明：

1. dataSet：传入的样本集
2. index：指定特征列的索引
3. value：指定特征的某一特征值
4. sample：dataSet的具体样本
5. reducedSample：去除value后的具体样本（该样本sample[index]==value）
6. retDataSet：按指定某一特征值划分出的样本子集

4.4 选取当前样本集下的最优划分特征索引：

#? 选取当前样集下的最优划分特征索引
#  返回最优划分特征的索引 bestFeatureIndex
def chooseBestFeatureToSplit(dataSet):
    featureCounts=len(dataSet[0])-1     # 获取当前样本集的特征个数，-1是因为最后一列是标签
    baseEnt=calEnt(dataSet)             # 计算当前样本集的信息熵Ent(D)
    bestGain=0.0;bestFeatureIndex=-1    # 初始化最优信息增益bestGain、最优特征bestFeature
    for i in range(featureCounts):      # 遍历每个特征，求各自的信息增益Gain
        featValList=[sample[i] for sample in dataSet]   # 第i个特征下所有样本出现的特征值（有重复）
        uniqueVals=set(featValList)                     # 第i个特征的可能特征值（无重复）
        newEnt=0.0          # 初始化信息熵
        for value in uniqueVals:
            subDataSet=splitDataSet(dataSet,i,value)    # 根据特定的特征值value划分出的样本子集
            pro=len(subDataSet)/float(len(dataSet))     # 划分出的样本子集占总样本数的比例
            newEnt+=pro*calEnt(subDataSet)              # 计算各特征值的熵并加和
        Gain=baseEnt-newEnt                             # 计算信息增益Gain(D,a)
        if(Gain>bestGain):      # 求最大的信息增益Gain
            bestGain=Gain
            bestFeatureIndex=i  # 获取最优划分特征的索引
    return bestFeatureIndex

函数作用：计算各特征的信息增益Gain(dataset,feature)，从而选出最优划分特征bestFeature，最后返回最优划分特征的索引bestFeatureIndex；

变量说明：

1. dataSet：传入的样本集
2. featureCounts：当前样本集中特征的个数
3. baseEnt：当前样本集的熵 Ent(D)
4. bestGain：各特征中最大的信息增益 Gain(dataSet,bestFeature)
5. bestFeatureIndex：最优划分特征的索引列号
6. sample[i]：具体样本第i个特征值
7. featureValList：第i个特征下所有样本中出现的特征值（有重复值）
8. uniqueVals：第i个特征的可能特征值（无重复值）
9. newEnt：不同特征值下的熵 Ent(Di)
10. subDataSet：根据特定的特征值value划分出的样本子集
11. pro：样本子集占总样本数的比例
12. Gain：各个特征的信息增益Gain(D,a)

4.5 求样本集中出现次数最多的标签：

#? 求样本集中出现次数最多的标签
#  用于叶子节点的取值，返回样本集中出现次数最多的标签 sortedLabelCounts[0][0]
import operator
def majorLabel(labelList):
    labelCounts={}      # key为标签（好瓜/坏瓜），value为标签在labelList中出现的次数
    for label in labelList:     # 遍历所有样本的标签
        if label not in labelCounts.keys(): # 如果该标签不在labelCounts的key值中
            labelCounts[label]=0            # 则增加该key值，并赋初值=0
        labelCounts[label]+=1               # 对labelCounts中已有的标签计数+1
    sortedLabelCounts=sorted(labelCounts.items(),key=operator.itemgetter(1),reverse=True)   # 根据value值逆序排序labelCounts
    return sortedLabelCounts[0][0]          # 返回第一个元素的第一个元素（标签）

函数作用：选取叶子结点的取值，返回样本集中出现次数最多的标签（好瓜/坏瓜）sortedLabelCounts[0][0]；

变量说明：

1. labelList：返回样本集中所有样本的标签（有重复值）
2. labelCounts：字典，key为标签，value为该标签key在labelList中出现的次数
3. label：具体标签（好瓜/坏瓜）
4. labelCounts.keys()：labelCounts的key值
5. labelCounts[label]：labelCounts中key值==label对应的value值
6. sortedLabelCounts：根据value值，逆序排列labelCounts字典
7. sotredLabelCounts[0][0]：样本集中出现次数最多的标签

4.6 递归生成决策树：

#? 生成决策树 主方法
#  递归生成决策树 decisionTree
#  递归是逐级由深向浅的返回
def createTree(dataSet,labels):
    labelList=[sample[-1] for sample in dataSet]    # 返回当前样本集dataSet中所有样本的标签（有重复值列表）
    # 跳出递归，生成叶子节点（好瓜/坏瓜）
    if labelList.count(labelList[0])==len(labelList):   # 如果labelList中的标签完全相同
        return labelList[0]                             # 则直接返回该标签
    if len(dataSet[0])==1:              # 如果当前样本集dataSet的样本长度==1（只剩最后一列标签，无特征可供继续划分又不满足所有标签相同）
        return majorLabel(labelList)    # 就返回出现次数最多的标签作为叶子节点
    
    bestFeatureIndex=chooseBestFeatureToSplit(dataSet)  # 获取当前样本集dataSet最优划分特征的索引
    bestFeature=labels[bestFeatureIndex]                # 获取当前样本集dataSet的最优划分特征
    decisionTree={bestFeature:{}}   # 字典存储决策树的信息
    del(labels[bestFeatureIndex])   # 删除已经选出的特征
    featureVals=[sample[bestFeatureIndex] for sample in dataSet] # 样本集中所有样本中的最优特征对应的特征值组成的列表（有重复值）
    uniqueVals=set(featureVals)     # 最优特征对应的所有可能取值（无重复值）
    for value in uniqueVals:        # 遍历最优特征所有可能的取值value
        subLabels=labels[:]         # 将最优特征去除后的特征列表传递给subLabels
        decisionTree[bestFeature][value]=createTree(splitDataSet(dataSet,bestFeatureIndex,value),subLabels)  # 递归生成decisionTree
    return decisionTree

函数作用：递归生成决策树 decisionTree

变量说明：

1. dataSet：传入的样本集
2. labels：传入的特征列表
3. labelList：存放样本集dataSet中所有样本的标签（有重复值）
4. sample：样本集的具体样本
5. labelList[0]：第一个样本的标签
6. dataSet[0]：样本集中的第一个样本
7. majorLabel(labelList)：样本集中出现次数最多的标签
8. bestFeatureIndex：当前样本集中最优划分特征的索引列
9. bestFeature：当前样本集中最优的划分特征
10. labels[bestFeatureIndex]：最优划分特征索引对应的具体特征
11. decisionTree：生成的决策树
12. featureVals：样本集dataSet中最优特征对应的所有特征值（有重复值）
13. uniqueVals：最优特征对应的可能取值（无重复值）
14. value：最优特征对应的具体取值
15. subLabels：去除最优特征后的特征列表

4.7 对决策样本进行分类：

#? 对验证样本进行分类
#  返回一个对样本分类后的标签classLabel
def classify(decisionTree,features,testSample):
	rootFeature=list(decisionTree.keys())[0]        # rootFeature：根节点是何种特征
	rootDict=decisionTree[rootFeature]              # rootDict为根节点的value值，是一个字典
	rootFeatureIndex=features.index(rootFeature)    # 获取根节点在特征列表中的索引
	for value in rootDict.keys():               # value为特征rootFeature的不同取值，并遍历value
		if testSample[rootFeatureIndex]==value:     # 如果待测样本的该特征的特征值==value
			if type(rootDict[value])==dict:     # 如果该特征值value对应的value'是一个字典
				classLabel=classify(rootDict[value],features,testSample)    # 则需要递归继续向决策树的下面结点查询
			else:                               # 如果该特征值value对应的value'是一个单独的值（标签）
				classLabel=rootDict[value]      # 则该值就是要找的标签
	return classLabel   # 返回该样本testSample的标签

函数作用：对传入的待测样本testSample根据已生成的决策树decisionTree计算出该样本的标签（好瓜/坏瓜），返回该标签 classLabel

变量说明：

1. decisionTree：某一结点出发的决策树
2. features：所有特征列表
3. testSample：待测试样本
4. decisionTree.keys()：（某一特征值下）对应根结点
5. decisionTree[rootFeature]：根节点对应的各个分支，字典
6. rootFeature：根节点（如纹理）
7. rootDict：根节点下的分支，字典（纹理结点对应的三个分支：模糊、清晰、稍糊）
8. rootFeatureIndex：节点在特征列表features中的索引；
9. value：以根节点为特征的不同特征取值（如模糊/清晰/稍糊）
10. testSample[rootFeatureIndex]：待测试样本中以根节点为特征对应的具体特征值
11. rootDict[value]：具体特征值对应的value（可能是一个字典/标签）
12. classLabel：该待测试样本计算出的标签

4.8 执行：

if __name__=='__main__':    # 如果在当前模块/文件下执行，将会指定下述代码
    dataSet, labels=createDataSet()
    decisionTree=createTree(dataSet, labels)
    print(f"\ndecisionTree={decisionTree}\n")     # 输出决策树模型结果
    # 验证集
    features=  ['色泽','根蒂','敲声','纹理','脐部','触感']  # 特征列表     
    testSample=['浅白','蜷缩','浊响','清晰','凹陷','硬滑']  # 待测样本
    print(f"测试结果1sampleLabel= {classify(decisionTree,features,testSample)}\n")   # 输出测试结果

    features=  ['色泽','根蒂','敲声','纹理','脐部','触感']  # 特征列表     
    testSample=['浅白','硬挺','清脆','模糊','平坦','硬滑']  # 待测样本
    print(f"测试结果2sampleLabel= {classify(decisionTree,features,testSample)}\n")   # 输出测试结果

    features=  ['色泽','根蒂','敲声','纹理','脐部','触感']  # 特征列表     
    testSample=['浅白','蜷缩','浊响','模糊','平坦','硬滑']  # 待测样本
    print(f"测试结果3sampleLabel= {classify(decisionTree,features,testSample)}\n")   # 输出测试结果

函数说明：执行主函数代码，利用上述各函数打印出最终的决策树decisionTree并且对验证集待测样本进行测试检验

变量说明：

1. features：特征列表
2. testSample：待测试样本

4.9 运行结果：

decisionTree={'纹理': {'稍糊': {'触感': {'硬滑': '坏瓜', '软粘': '好瓜'}}, '清晰': {'根蒂': {'硬挺': '坏瓜', '蜷缩': '好瓜', '稍蜷': {'色泽': {'青绿': '好瓜', '乌黑': {'触感': {'硬滑': '好瓜', '软粘': '坏瓜'}}}}}}, '模糊': '坏瓜'}}     

测试结果1sampleLabel= 好瓜

测试结果2sampleLabel= 坏瓜

测试结果3sampleLabel= 坏瓜

决策树decisionTree：

{'纹理': 
    {'模糊': '坏瓜', 
     '清晰': {'根蒂': 
                {'稍蜷': {'色泽': 
                            {'乌黑': {'触感': 
                                        {'软粘': '坏瓜', 
                                         '硬滑': '好瓜'}}, 
                             '青绿': '好瓜'}}, 
                 '硬挺': '坏瓜', 
                 '蜷缩': '好瓜'}}, 
     '稍糊': {'触感': 
                {'软粘': '好瓜', 
                 '硬滑': '坏瓜'}}}}

可视化为树状结构为：

4.10 实现决策树的总代码：文章来源地址https://www.toymoban.com/news/detail-491360.html

#! Decision Tree(ID3算法 信息增益Gain)

#? 构建数据集
#  返回一个元组 (dataSet,labels)
def createDataSet():    # 创造示例数据
    dataSet=[['青绿','蜷缩','浊响','清晰','凹陷','硬滑','好瓜'],
             ['乌黑','蜷缩','沉闷','清晰','凹陷','硬滑','好瓜'],
             ['乌黑','蜷缩','浊响','清晰','凹陷','硬滑','好瓜'],
             ['青绿','蜷缩','沉闷','清晰','凹陷','硬滑','好瓜'],                
             ['青绿','稍蜷','浊响','清晰','稍凹','软粘','好瓜'],               
             ['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','好瓜'],                
             ['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','好瓜'],
             
             ['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','坏瓜'],
             ['青绿','硬挺','清脆','清晰','平坦','软粘','坏瓜'],
             ['浅白','蜷缩','浊响','模糊','平坦','软粘','坏瓜'],
             ['青绿','稍蜷','浊响','稍糊','凹陷','硬滑','坏瓜'],  
             ['浅白','稍蜷','沉闷','稍糊','凹陷','硬滑','坏瓜'],
             ['乌黑','稍蜷','浊响','清晰','稍凹','软粘','坏瓜'],
             ['青绿','蜷缩','沉闷','稍糊','稍凹','硬滑','坏瓜']]
    labels = ['色泽','根蒂','敲声','纹理','脐部','触感']  #六个特征
    return dataSet,labels

#? 计算信息熵
#  返回输入样本集dataSet的信息熵 Ent
from math import log
def calEnt(dataSet):
    sampleCounts=len(dataSet)   # 样本集的样本数
    labelCounts={}              # key为标签值label（好瓜、坏瓜），value为对应标签key在样本集中出现的次数
    for sample in dataSet:      # 遍历样本集dataSet中每个样本sample
        label=sample[-1]        # 标签label为样本sample的最后一个元素值
        if label not in labelCounts.keys():     # 如果该标签label不在字典labelCounts的key值中
            labelCounts[label]=0                # 则新增该key，并赋初值0
        labelCounts[label]+=1   # 对遍历到的每个sample统计其所属标签的个数
    Ent=0.0     # 信息熵初始化
    for key in labelCounts:
        pro=float(labelCounts[key])/sampleCounts    # 具体标签占总样本数的比例pro
        Ent-=pro*log(pro,2)     # 计算样本集dataSet的信息熵Ent
    return Ent

#? 按给定特征值划分出样本子集
#  指定特征列的索引index，对特征值==value的样本划分出来为一个样本子集retDataSet，并对这些样本的value去掉，返回样本子集 retDataSet
def splitDataSet(dataSet,index,value):      # index是指定特征列的索引，value是该特征下的某一特征值
    retDataSet=[]
    for sample in dataSet:                  # 遍历样本集dataSet中的具体样本sample
        if sample[index]==value:            # 找到目标特征值value的索引
            # 去除特征值==value这些样本的vlaue值
            reducedSample=sample[:index]            # 剪下目标索引前的列表
            reducedSample.extend(sample[index+1:])  # 将目标索引后的列表添加到索引前列表的后面
            retDataSet.append(reducedSample)        # 将sample[index]==value并去除该vlaue的样本添加到retDataSet样本集中
    return retDataSet

#? 选取当前样集下的最优划分特征索引
#  返回最优划分特征的索引 bestFeatureIndex
def chooseBestFeatureToSplit(dataSet):
    featureCounts=len(dataSet[0])-1     # 获取当前样本集的特征个数，-1是因为最后一列是标签
    baseEnt=calEnt(dataSet)             # 计算当前样本集的信息熵Ent(D)
    bestGain=0.0;bestFeatureIndex=-1    # 初始化最优信息增益bestGain、最优特征bestFeature
    for i in range(featureCounts):      # 遍历每个特征，求各自的信息增益Gain
        featValList=[sample[i] for sample in dataSet]   # 第i个特征下所有样本出现的特征值（有重复）
        uniqueVals=set(featValList)                     # 第i个特征的可能特征值（无重复）
        newEnt=0.0          # 初始化信息熵
        for value in uniqueVals:
            subDataSet=splitDataSet(dataSet,i,value)    # 根据特定的特征值value划分出的样本子集
            pro=len(subDataSet)/float(len(dataSet))     # 划分出的样本子集占总样本数的比例
            newEnt+=pro*calEnt(subDataSet)              # 计算各特征值的熵并加和
        Gain=baseEnt-newEnt                             # 计算信息增益Gain(D,a)
        if(Gain>bestGain):      # 求最大的信息增益Gain
            bestGain=Gain
            bestFeatureIndex=i  # 获取最优划分特征的索引
    return bestFeatureIndex

#? 求样本集中出现次数最多的标签
#  用于叶子节点的取值，返回样本集中出现次数最多的标签 sortedLabelCounts[0][0]
import operator
def majorLabel(labelList):
    labelCounts={}      # key为标签（好瓜/坏瓜），value为标签在labelList中出现的次数
    for label in labelList:     # 遍历所有样本的标签
        if label not in labelCounts.keys(): # 如果该标签不在labelCounts的key值中
            labelCounts[label]=0            # 则增加该key值，并赋初值=0
        labelCounts[label]+=1               # 对labelCounts中已有的标签计数+1
    sortedLabelCounts=sorted(labelCounts.items(),key=operator.itemgetter(1),reverse=True)   # 根据value值逆序排序labelCounts
    return sortedLabelCounts[0][0]          # 返回第一个元素的第一个元素（标签）

#? 生成决策树 主方法
#  递归生成决策树 decisionTree
#  递归是逐级由深向浅的返回
def createTree(dataSet,labels):
    labelList=[sample[-1] for sample in dataSet]    # 返回当前样本集dataSet中所有样本的标签（有重复值列表）
    # 跳出递归，生成叶子节点（好瓜/坏瓜）
    if labelList.count(labelList[0])==len(labelList):   # 如果labelList中的标签完全相同
        return labelList[0]                             # 则直接返回该标签
    if len(dataSet[0])==1:              # 如果当前样本集dataSet的样本长度==1（只剩最后一列标签，无特征可供继续划分又不满足所有标签相同）
        return majorLabel(labelList)    # 就返回出现次数最多的标签作为叶子节点
    
    bestFeatureIndex=chooseBestFeatureToSplit(dataSet)  # 获取当前样本集dataSet最优划分特征的索引
    bestFeature=labels[bestFeatureIndex]                # 获取当前样本集dataSet的最优划分特征
    decisionTree={bestFeature:{}}   # 字典存储决策树的信息
    del(labels[bestFeatureIndex])   # 删除已经选出的特征
    featureVals=[sample[bestFeatureIndex] for sample in dataSet] # 样本集中所有样本中的最优特征对应的特征值组成的列表（有重复值）
    uniqueVals=set(featureVals)     # 最优特征对应的所有可能取值（无重复值）
    for value in uniqueVals:        # 遍历最优特征所有可能的取值value
        subLabels=labels[:]         # 将最优特征去除后的特征列表传递给subLabels
        decisionTree[bestFeature][value]=createTree(splitDataSet(dataSet,bestFeatureIndex,value),subLabels)  # 递归生成decisionTree
    return decisionTree

     
#? 对验证样本进行分类
#  返回一个对样本分类后的标签classLabel
def classify(decisionTree,features,testSample):
	rootFeature=list(decisionTree.keys())[0]        # rootFeature：根节点是何种特征
	rootDict=decisionTree[rootFeature]              # rootDict为根节点的value值，是一个字典
	rootFeatureIndex=features.index(rootFeature)    # 获取根节点在特征列表中的索引
	for value in rootDict.keys():               # value为特征rootFeature的不同取值，并遍历value
		if testSample[rootFeatureIndex]==value:     # 如果待测样本的该特征的特征值==value
			if type(rootDict[value])==dict:     # 如果该特征值value对应的value'是一个字典
				classLabel=classify(rootDict[value],features,testSample)    # 则需要递归继续向决策树的下面结点查询
			else:                               # 如果该特征值value对应的value'是一个单独的值（标签）
				classLabel=rootDict[value]      # 则该值就是要找的标签
	return classLabel   # 返回该样本testSample的标签



if __name__=='__main__':    # 如果在当前模块/文件下执行，将会指定下述代码
    dataSet, labels=createDataSet()
    decisionTree=createTree(dataSet, labels)
    print(f"\ndecisionTree={decisionTree}\n")     # 输出决策树模型结果
    # 验证集
    features=  ['色泽','根蒂','敲声','纹理','脐部','触感']  # 特征列表     
    testSample=['浅白','蜷缩','浊响','清晰','凹陷','硬滑']  # 待测样本
    print(f"测试结果1sampleLabel= {classify(decisionTree,features,testSample)}\n")   # 输出测试结果

    features=  ['色泽','根蒂','敲声','纹理','脐部','触感']  # 特征列表     
    testSample=['浅白','硬挺','清脆','模糊','平坦','硬滑']  # 待测样本
    print(f"测试结果2sampleLabel= {classify(decisionTree,features,testSample)}\n")   # 输出测试结果

    features=  ['色泽','根蒂','敲声','纹理','脐部','触感']  # 特征列表     
    testSample=['浅白','蜷缩','浊响','模糊','平坦','硬滑']  # 待测样本
    print(f"测试结果3sampleLabel= {classify(decisionTree,features,testSample)}\n")   # 输出测试结果

到了这里，关于ID3决策树及Python实现（详细）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！