3.3 伴随矩阵法求逆矩阵-Toy模板网

这篇具有很好参考价值的文章主要介绍了3.3 伴随矩阵法求逆矩阵。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

逆矩阵定义

逆矩阵指的是另一个矩阵和自己相乘会变成单位矩阵，符号是右上角一个 $- 1$ ，就是：
$AA^{-1}=A^{-1}A=I$
例如以下两个矩阵就是互为逆矩阵：
$\begin{pmatrix}-1 & 1 & 0 & 0\\ -3 & 2 & 1 & 0\\ 1 & 1 & 0 & -1\\ 4 & -4 & -1 & 1\\ \end{pmatrix}\begin{pmatrix}1 & 1 & 1 & 1\\ 2 & 1 & 1 & 1\\ -1 & 2 & 1 & 1\\ 3 & 2 & 1 & 2\\ \end{pmatrix}= \begin{pmatrix}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix}$

伴随矩阵

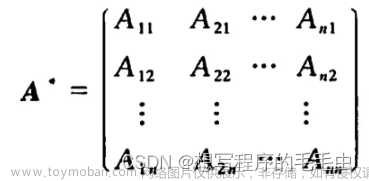
求逆矩阵最死板的办法就是伴随矩阵法了。这种算法因为计算量超级大，所以性能比较低，不建议使用，但是我还是要讲讲。首先，什么是伴随矩阵adjugate matrix呢？伴随矩阵符号是一个*号，是由每个元素的代数余子式组成的矩阵的转置（千万不要忘了转置啊）。矩阵A的第i行第j列的代数余子式cofactor记作 $A_{ij}$ ，所以伴随矩阵的定义如下：
$A^*=\begin{pmatrix}A_{11} & \cdots & A_{1n}\\ \vdots & \ddots & \vdots\\ A_{n1} & \cdots & A_{nn} \end{pmatrix}^T =\begin{pmatrix}A_{11} & \cdots & A_{n1}\\ \vdots & \ddots & \vdots\\ A_{1n} & \cdots & A_{nn} \end{pmatrix}$
把伴随矩阵除于行列式就是矩阵A的逆矩阵了：
$A^{-1}=\frac1{|A|}A^*$

python实现

这种计算逆矩阵的方法用Python很容易写出来：

     # 子式
    def minor(self, row, column):
        # 创建新矩阵
        n = len(self.__lines)
        array = [[0 for _ in range(n - 1)] for _ in range(n - 1)]
        # i 代表行 j代表列
        for i in range(0, n - 1):
            for j in range(0, n - 1):
                col = j if j < column else j + 1
                r = i if i < row else i + 1
                array[j][i] = self.__lines[col][r]
        return Matrix(array).chio()

    # 求代数余子式
    def cofactor(self, row, column):
        minor = self.minor(row, column)
        return minor if (row + column) % 2 == 0 else -minor

    # 用伴随矩阵求逆矩阵
    def inverse(self):
        det = self.chio()
        n = len(self.__lines)
        array = [[0 for _ in range(n)] for _ in range(n)]
        for i in range(0, n):
            for j in range(0, n):
                array[i][j] = self.cofactor(j, i) / det
        matrix = Matrix(array)
        return Matrix(matrix.transpose())

测试数据：
$\begin{pmatrix}1 & 1 & 1 & 1\\ 2 & 1 & 1 & 1\\ -1 & 2 & 1 & 1\\ 3 & 2 & 1 & 2\\ \end{pmatrix} \begin{pmatrix}-1 & 1 & 0 & 0\\ -3 & 2 & 1 & 0\\ 1 & 1 & 0 & -1\\ 4 & -4 & -1 & 1\\ \end{pmatrix}= \begin{pmatrix}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix}$ 文章来源地址https://www.toymoban.com/news/detail-491763.html