C++基础：二维费用的背包问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了C++基础：二维费用的背包问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

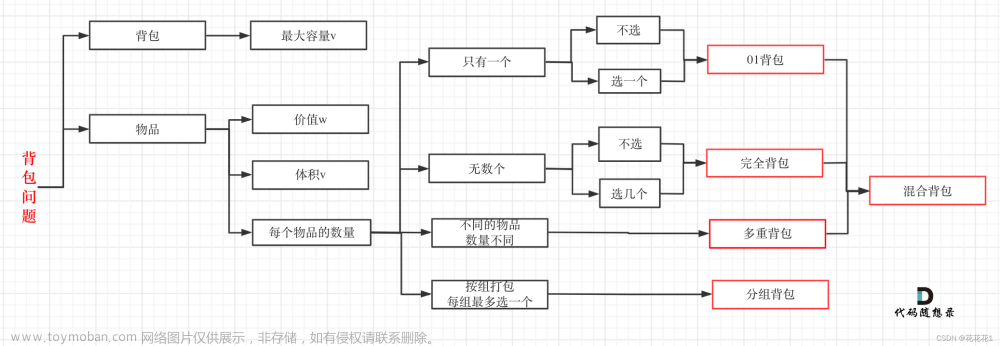
注意：如果你还没搞定（指的是真正理解）01背包，请不要看。看了脑壳更晕

什么是二维费用的背包问题？请看AcWing上的一道题：

有 N 件物品和一个容量是 V 的背包，背包能承受的最大重量是 M。

每件物品只能用一次。体积是 vi，重量是 mi，价值是 wi。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。

输入格式

第一行三个整数，N,V,M，用空格隔开，分别表示物品件数、背包容积和背包可承受的最大重量。

接下来有 N 行，每行三个整数 vi,mi,wi，用空格隔开，分别表示第 i 件物品的体积、重量和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N≤10000
0<V,M≤1000
0<vi,mi≤1000
0<wi≤10000

输入样例
4 5 6
1 2 3
2 4 4
3 4 5
4 5 6
输出样例：
8

这就是典型的二维费用背包问题。

首先考虑01背包转移方程：dp[i][j]=max(dp[i-1][j],dp[i-1][j-c[i]]+w[i])，这只有一个费用

那我们如何表示两个费用？

一种思路保存原有的状态(dp[i][j])、方程，选取一个费用优先满足条件，并求出此时的价值，再看另一个费用是否满足条件。但小编躬行证明这真的很难办，写出来的程序也有漏洞

所以就只能改变状态了

我们设dp[i][j][k]表示在前i个物品中选取、满足费用1的限制且满足费用2的限制的最大价值

是不是跟01背包很像？（01：dp[i][j]前i个物品中选取且满足费用的限制的最大价值）

如果你理解了01背包，状态转移方程应该就很好想了：

dp[i][j][k]=max(dp[i-1][j][k],dp[i-1][j-c1[i]][k-c2[i]]+w[i]);

然后我们像优化01一样优化上述方程（注意循环要变顺序的哟(＾Ｕ＾)ノ~ＹＯ）：

dp[j][k]=max(dp[j][k],dp[j-c1[i]][k-c2[i]]+w[i]);

代码：

#include<iostream>
#include<cstdio>
#define _for(i,a,b) for (int i=(a);i<(b);i++)//宏定义，懒人专用
using namespace std;
const int N=1e2+5,M=1e2+5;
int dp[N][M];
int main(){
    int n,v1,v2;
    cin>>n>>v1>>v2;
    _for(i,0,n){
        int c1,c2,w;
        cin>>c1>>c2>>w;
        for (int j=v1;j>=c1;j--){//注意枚举顺序   b
            for (int k=v2;k>=c2;k--){//a
                dp[j][k]=max(dp[j][k],dp[j-c1][k-c2]+w);
            }
        }
    }
    cout<<dp[v1][v2]<<endl;
    return 0;
}
//其实可以来一个#define _rep(i,a,b) for (int i=(a);i>=(b);i--)来替换a、b代码

下面举一道变形题（裸题）：

C++基础：二维费用的背包问题