chatgpt-AIGC-从数学开始-Toy模板网

这篇具有很好参考价值的文章主要介绍了chatgpt-AIGC-从数学开始。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

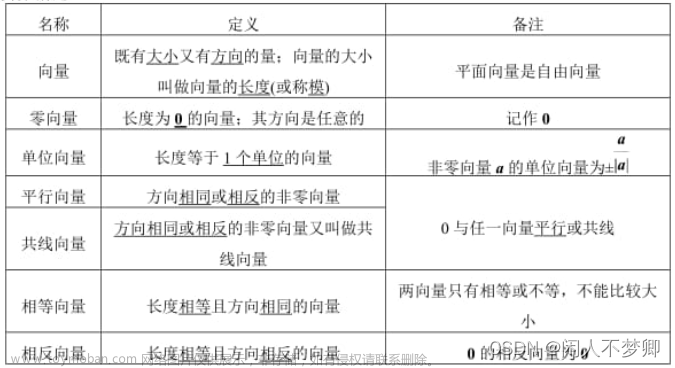
向量

向量是由n个实数组成的一个n行1列（n*1）或一个1行n列（1*n）的有序数组；

点积

- 向量的点乘,也叫向量的内积、数量积，对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量。

点积几何意义

- 点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在b向量在a向量方向上的投影

叉乘

- 两个向量的叉乘，又叫向量积、外积、叉积，叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。

叉乘的几何意义

- 在3D图像学中，叉乘的概念非常有用，可以通过两个向量的叉乘，生成第三个垂直于a，b的法向量，从而构建X、Y、Z坐标系。

参考文档

- https://blog.csdn.net/dcrmg/article/details/52416832 (向量点乘（内积）和叉乘（外积、向量积）概念及几何意义解读)

矩阵

特征值和特征向量

- 由于矩阵可以看做是向量的集合,因此一个矩阵(m*n)可以看做是通过n个m维向量,形成的一个向量,因此可以转换为通过特征向量构建一个基本的m维坐标系,通过特征值对这m维向量进行伸缩 ,即归一化 (normal)

svd分解 - 奇异值分解(Singular Value Decomposition，以下简称SVD)

- 将任一矩阵(m*n) 拆解成三个矩阵 U , V ,R,其中U,V是正定矩阵(正定矩阵的逆矩阵=正定矩阵的转置矩阵),通过svd分解,可以达到降维的效果,其中svd分解也是pca (主成分分析（Principal Component Analysis,简称 PCA) 的前置条件

chatgpt-AIGC-从数学开始

参考文档

- https://zhuanlan.zhihu.com/p/524126772 (从数学的角度浅谈特征值和特征向量的求法)

- https://zhuanlan.zhihu.com/p/31386807 (四）矩阵的特征分解与奇异值分解(SVD))

- https://blog.csdn.net/OrdinaryMatthew/article/details/117948620 (PAC、SVD以及它们的联系之充分数学知识推导)

机器学习的基本概念

张量

- n维矩阵的统称

参考文档

- https://zhuanlan.zhihu.com/p/48982978 (笔记 | 什么是张量（tensor）& 深度学习)

激活函数,损失函数,动量法的原理

chatgpt-AIGC-从数学开始

参考文档

- https://baijiahao.baidu.com/s?id=1574592152285995 (为了彻底理解深度学习，我们到底需要掌握哪些数学知识呢)

神经网络demo

import java.util.Random;
public class BpDeep{
    public double[][] layer;//神经网络各层节点
    public double[][] layerErr;//神经网络各节点误差
    public double[][][] layer_weight;//各层节点权重
    public double[][][] layer_weight_delta;//各层节点权重动量
    public double mobp;//动量系数
    public double rate;//学习系数

    public BpDeep(int[] layernum, double rate, double mobp){
        this.mobp = mobp;
        this.rate = rate;
        layer = new double[layernum.length][];
        layerErr = new double[layernum.length][];
        layer_weight = new double[layernum.length][][];
        layer_weight_delta = new double[layernum.length][][];
        Random random = new Random();
        for(int l=0;l<layernum.length;l++){
            layer[l]=new double[layernum[l]];
            layerErr[l]=new double[layernum[l]];
            if(l+1<layernum.length){
                layer_weight[l]=new double[layernum[l]+1][layernum[l+1]];
                layer_weight_delta[l]=new double[layernum[l]+1][layernum[l+1]];
                for(int j=0;j<layernum[l]+1;j++)
                    for(int i=0;i<layernum[l+1];i++)
                        layer_weight[l][j][i]=random.nextDouble();//随机初始化权重
            }   
        }
    }
    //逐层向前计算输出
    public double[] computeOut(double[] in){
        for(int l=1;l<layer.length;l++){
            for(int j=0;j<layer[l].length;j++){
                double z=layer_weight[l-1][layer[l-1].length][j];
                for(int i=0;i<layer[l-1].length;i++){
                    layer[l-1][i]=l==1?in[i]:layer[l-1][i];
                    z+=layer_weight[l-1][i][j]*layer[l-1][i];
                }
                layer[l][j]=1/(1+Math.exp(-z));
            }
        }
        return layer[layer.length-1];
    }
    //逐层反向计算误差并修改权重
    public void updateWeight(double[] tar){
        int l=layer.length-1;
        for(int j=0;j<layerErr[l].length;j++)
            layerErr[l][j]=layer[l][j]*(1-layer[l][j])*(tar[j]-layer[l][j]);

        while(l-->0){
            for(int j=0;j<layerErr[l].length;j++){
                double z = 0.0;
                for(int i=0;i<layerErr[l+1].length;i++){
                    z=z+l>0?layerErr[l+1][i]*layer_weight[l][j][i]:0;
                    layer_weight_delta[l][j][i]= mobp*layer_weight_delta[l][j][i]+rate*layerErr[l+1][i]*layer[l][j];//隐含层动量调整
                    layer_weight[l][j][i]+=layer_weight_delta[l][j][i];//隐含层权重调整
                    if(j==layerErr[l].length-1){
                        layer_weight_delta[l][j+1][i]= mobp*layer_weight_delta[l][j+1][i]+rate*layerErr[l+1][i];//截距动量调整
                        layer_weight[l][j+1][i]+=layer_weight_delta[l][j+1][i];//截距权重调整
                    }
                }
                layerErr[l][j]=z*layer[l][j]*(1-layer[l][j]);//记录误差
            }
        }
    }

    public void train(double[] in, double[] tar){
        double[] out = computeOut(in);
        updateWeight(tar);
    }
}

import java.util.Arrays;
public class BpDeepTest{
    public static void main(String[] args){
        //初始化神经网络的基本配置
        //第一个参数是一个整型数组，表示神经网络的层数和每层节点数，比如{3,10,10,10,10,2}表示输入层是3个节点，输出层是2个节点，中间有4层隐含层，每层10个节点
        //第二个参数是学习步长，第三个参数是动量系数
        BpDeep bp = new BpDeep(new int[]{2,10,2}, 0.15, 0.8);

        //设置样本数据，对应上面的4个二维坐标数据
        double[][] data = new double[][]{{1,2},{2,2},{1,1},{2,1}};
        //设置目标数据，对应4个坐标数据的分类
        double[][] target = new double[][]{{1,0},{0,1},{0,1},{1,0}};

        //迭代训练5000次
        for(int n=0;n<5000;n++)
            for(int i=0;i<data.length;i++)
                bp.train(data[i], target[i]);

        //根据训练结果来检验样本数据
        for(int j=0;j<data.length;j++){
            double[] result = bp.computeOut(data[j]);
            System.out.println(Arrays.toString(data[j])+":"+Arrays.toString(result));
        }

        //根据训练结果来预测一条新数据的分类
        double[] x = new double[]{3,1};
        double[] result = bp.computeOut(x);
        System.out.println(Arrays.toString(x)+":"+Arrays.toString(result));
    }
}