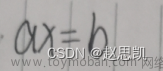之前线性代数里一直提到，对于一个线性变换，我们需要找到一个基或者两个基，让这个线性变换足够简单。那么问题来了，如果我先给出一个矩阵呢？
这个时候我们看到的更多的是矩阵分解的理论，谱分解和奇异值分解。但是似乎很少有结合去理解的。这里我想看一下。
首先我们需要看这篇：
如何理解相似矩阵？ - 知乎
这里我觉得他讲的不够清晰，应该这么讲，假设存在某一个线性变换： T，在空间V2下，可以将v'变为Bv'. 而假设我们经历这么一个过程。
首先我们将v'用矩阵P转成V1下的点v，然后用同样的线性变换T，变成APv'.注意，因为是在不同的空间下，所以同样的线性变换会展现出不同的矩阵，最后，我们再将空间变回去，这样就有了
Bv' = P-1APv' 于是B=P-1AP， 我们看到，同样的线性变换在不同的空间下的关系。
所以，让我们梳理下：
首先是可对角化的线性变换的几个等价条件：
核心在于V有由T的本征向量构成的基。于是，在空间V下，我们的线性变换T的矩阵是A，那么因为它有本征向量构成的基，我们可以认为：
根据前面学习到的相似矩阵，我们知道A和对角阵相似。所以他们应该是在不同的基下的矩阵。
注意，即便他们在不同的基下，他们代表的空间V是一样的。（这和我们前面举例的V1，V2概念不同）
按照前面相似矩阵的理解，我们知道S表示的是特征向量基到标准基（就是A所在的基）下面的变换。
所以，S就是特征向量构成的列。完美符合。
这样我们就理解了第一个问题，对角化和特征向量分解。
然后是第二个问题，我们先理解下定义：
其实伴随的直观解释非常难理解，但其实从我们之前对偶空间的就能联想，就是转置。矩阵的转置往往联系着映射的反转。
这里我们不深入讨论，只是要记住这个结论。
看完这些无聊的概念，关键的来了：
这里我们需要开始理解为什么正规会和可对角化扯上关系。前面我们提到了伴随的一个重要特征是它的矩阵是原矩阵的共轭转置，而对角矩阵的共轭转置的特点是，只需要共轭了，转置啥都没做。于是这样就把正规--->伴随---->转置---->对角联系到了一起。
实普定理的证明的联想是一样的，同样是共轭转置，而且因为是实数，共轭就是本身。更加纯粹。
证明过程也不深入了。
这样我们理解了第二个问题：什么情况下他是可以对角化。
接下来是第三个问题：对于不同基的算子：
等距同构给我的感觉就是这个矩阵变换并不改变这个向量的长度。
考虑伴随：
可以想象，伴随和它自己是互逆的。
这是一份总结，伴随算子对应的是矩阵的转置。记住，算子本身是线性映射，然后选取了一个基，会产生矩阵。
然后可以对角化的矩阵说的是要找一组基，让这个矩阵可以对角化。然后就有了自伴算子和正规算子，分别对应实数域和复数域。
为什么要研究对角阵呢，因为他足够简单，是单纯的伸缩变换。
所以正交矩阵（实数域）酉矩阵（复数域）他们都是对角矩阵修改了基之后的新表示而已。
极分解感觉过于复杂了，就不深入了解说明了。
最后的高潮：奇异值分解
和前面类似，我们也需要对应矩阵分解来参考：
SVD奇异值分解的数学涵义及其应用实例 - 知乎
让我们来总结下：
对于一个线性变换T，我们有一个它在某个基下的矩阵A，遗憾的是这个矩阵不够好。于是我们思考换一个基，让他有一个足够好的矩阵。
于是先通过S^-1，将它变换到这个好的基（特征向量基）下，然后用一个很好的对角矩阵做变换，然后在通过S，给他换成原来的基。
同样，对于奇异值分解，也是先变换到第一个基下，用VT,然后进行对角矩阵，注意，这个时候的基是另个一基，然后又要变回原来的基。但这里我们发现一个问题，就是特征向量空间下，S和S的逆矩阵是很好理解的。但现在，两个基是不同的，我们从标准基转到第一个基的矩阵，其实是第一个基在标准基下的逆矩阵。这样似乎就没有特征向量空间那么直观。
但人类是聪明的：
仔细观察，就能发现，我们原始向量v，通过和标准基1（e1,e2....）的内积，那不就是对应的坐标吗？特征向量空间的时候其实也可以这么理解，不过直接用特征向量的逆矩阵看上去会更加方便而已。所以：
中间的对角矩阵，左边就是从标准基(f1,f2....)重新回到默认标准基。
先思考一个问题：
纯线性变换思考，一个T，变换一个向量v。我们把v换到另一个空间下，再经过同样的变换，再换回原来的空间下。在这种情况下，我们必须思考空间变换是矩阵，不引入矩阵的情况下，这个空间变换是很难让人理解的。
非矩阵形式的理解，只有这样：
考虑矩阵形式的理解。
对角矩阵的上边是第一个标准正交基(e1,e2....) 所以我们先要将默认基下的向量转到标准基下面的坐标，类似与一个坐标基的转换矩阵Ax.这时候可以有一个巧妙的变换，我们假定自己知道x在e1,e2下的坐标，那么直接对角阵*坐标本身即可。我们可以把e1,e2矩阵拆出来，那么右边显然就是
不过我感觉这里还是有点多余。对角阵左边也是同理。
这里我觉得很重要的一点是对角阵的左右两边都只代表了旋转，因为他们都是标准正交基，长度都是1.
求解的过程我们理解下就好：
文章来源：https://www.toymoban.com/news/detail-492073.html
我们只需要求出AAT的特征值分解，就可以得到奇异值分解的结果。文章来源地址https://www.toymoban.com/news/detail-492073.html
到了这里，关于结合理解矩阵和基的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
