动态规划刷题记录（1）-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划刷题记录（1）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

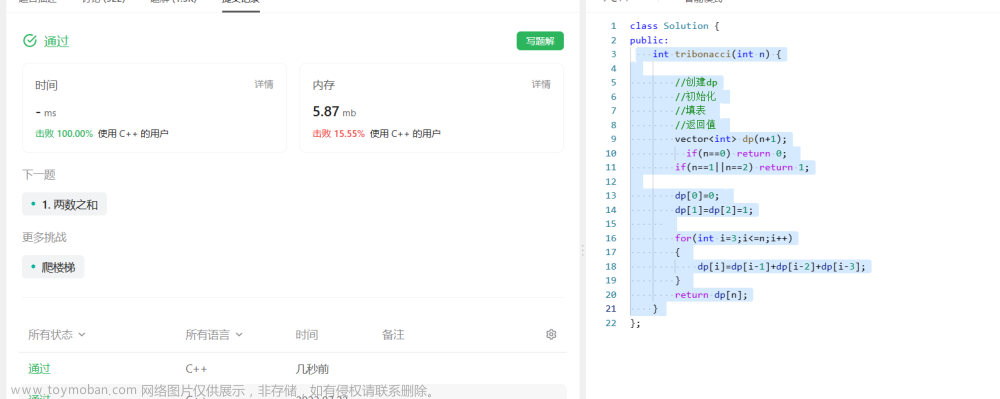
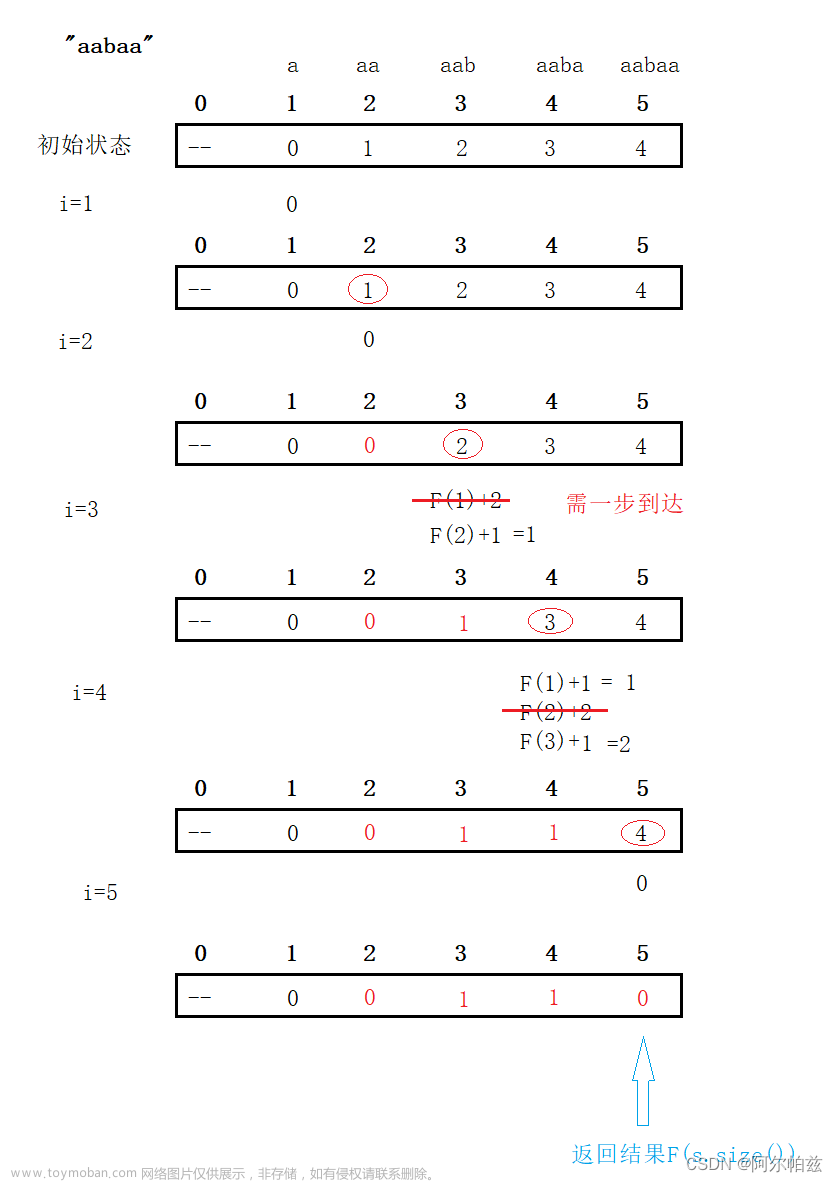
动态规划问题在这两年蓝桥杯频繁出现，它既是一个重点，也是一个难点。

1、整数拆分

动态规划刷题记录（1）

这道题目的思路其实很直接，基本上一眼就可以看出来这是完全背包问题的应用+一维优化。

整数N相当于是背包体积，2的幂相当于是物品体积，每种物品可以拿无数次，问你方案有多少种。数据范围已经给你了，我们可以确定最多用到2的20次方，因为2的21次方已经大于一百万了，于是我们先把2的前二十次方预处理。

接下来就是重点，我们定义集合f(i ，j)表示从前i个物品挑选使用，占用的体积为j的方案数，状态划分就是是否用了第i个物品？用了多少个？可能你没学过完全背包会看不懂我在说什么，背包问题作为动态规划的典型问题最好还是花时间学习

上代码：

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

#define N 1000100

const int mod = 1e9;

int n ,p[N];
int f[N];

int main()
{
    cin >> n;

    int t = 1;
    for (int i = 0 ;i <= 21 ;i ++) p[i] = t ,t *= 2;

    f[0] = 1;
    for (int i = 0 ;i <= 21 ;i ++)
        for (int j = p[i] ;j <= n ;j ++)
            f[j] = (f[j] + f[j - p[i]]) % mod;

    cout << f[n];
    return 0;
}

2、最大的和

动态规划刷题记录（1）

这道题目说白了就是让你在一行数中找到其中的两段，使这两段的和最大。这是一个动态规划问题，思路主要有两种：

（1）我们先来想想如果题目问你的是让你找到一个最大子段和，我们怎么解决？定义集合f(i)表示前i个数中的最大子段和，w[i]用来记录这n个数。那么以最大子段是否包含第i个数为集合划分依据：

区间不包含w[i]: f[i] = f[i - 1];
区间包含w[i]: f[i] = 以w[i - 1]结尾的最大连续区间和 + w[i];

那么很明显，我们缺少一个数据用来表示 以w[i - 1]结尾的最大连续区间和，所以我们再开一个区间h（i）用来记录以w[i]结尾的最大子段和。h(i)同样需要我们来递推：

区间只包含w[i]，也就是说a[i]一个数的和就大于了之前所有以w[i]结尾的子段和：h[i] = w[i];

区间包含了w[i]: h[i] = h[i - 1] + w[i];

到这里我们就可以解决找到一个最大子段和的问题了，那么现在再想想题目的求两段最大子段和。我们完全可以正着推一遍，再反着来一遍，最后枚举中间点在哪就行了。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;

#define N 1001000

int t ,f[N] ,h[N] ,g[N] ,w[N];

int main()
{
    cin >> t;
    while (t --)
    {
        int n;
        scanf("%d" ,&n);

        for (int i = 1 ;i <= n ; i ++) scanf("%d" ,&w[i]);//记录这n个数

        f[0] = g[0] = -1e9;//初始化数组，这里是个细节要注意，一般来说我们动态规划求最大值就需要初始化很小的数，求最小值就需要初始化一个很大的数。
        for (int i = 1 ;i <= n ;i ++)
        {
            h[i] = max(h[i - 1] ,0) + w[i];//其实就是h[i - 1] + w[i] 和 w[i]取最大值
            f[i] = max(f[i - 1] ,h[i]);//根据上面的递推公式
        }

        h[n + 1] = g[n + 1] = -1e9;//刚刚是1到n，现在我们n到1来一遍
        for (int i = n ;i >= 1 ;i --)
        {
            h[i] = max(h[i + 1] ,0) + w[i];
            g[i] = max(g[i + 1] ,h[i]);
        }

        int res = -1e9;
        for(int i = 1;i <= n;i ++) res = max(res, f[i] + g[i + 1]);//枚举断点，寻找最大值
        cout << res << endl;
    }

    return 0;
}

（2）第二种思路更好理解一点：f(i ,j ,0/1)表示考虑前 i个数，且已经选了 j个连续的子段，且第 i
个数是否在第 j 段中。文章来源地址https://www.toymoban.com/news/detail-492381.html

#include <algorithm>
#include <cstring>
#include <cstdio>
#include <iostream>

using namespace std;

#define N 50010

int f[N][3][2] ,a[N];

int main()
{
    int t;
    scanf("%d" ,&t);

    while (t --)
    {
        memset(f ,-0x3f ,sizeof(f));

        int n;
        scanf("%d" ,&n);

        f[0][0][0] = 0;
        for (int i = 1 ;i <= n ;i ++) scanf("%d" ,&a[i]);

        for (int i = 1 ;i <= n ; i ++)
        {
            for (int j = 0 ;j <= 2 ;j ++)
            {
                 f[i][j][1] = max(f[i - 1][j][1] + a[i] ,f[i][j][1]);//若选择第 i个数接在原先由第 i−1个数作为末尾的第 j段后面:
                 f[i][j][0] = max(max(f[i][j][1] ,f[i - 1][j][1]) ,f[i - 1][j][0]);//如果不选第i个数
                 if (j) f[i][j][1] = max(max(f[i - 1][j - 1][0] + a[i] ,f[i][j][1]) ,f[i - 1][j - 1][1] + a[i]);//如果第i个数单独开了一段
            }
        }

        cout << max(f[n][2][1] ,f[n][2][0]) << endl;
    } 
    return 0;

}

到了这里，关于动态规划刷题记录（1）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！