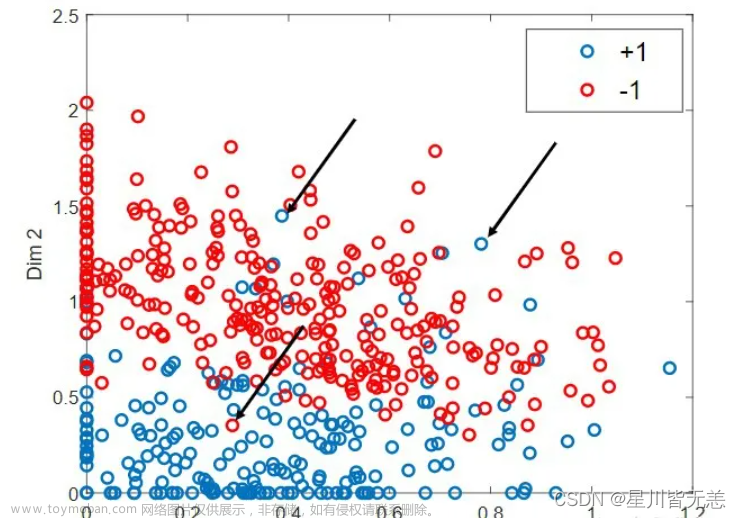
支持向量机（Support Vector Machine, SVM）从线性分类到核函数扩展-Toy模板网

这篇具有很好参考价值的文章主要介绍了支持向量机（Support Vector Machine, SVM）从线性分类到核函数扩展。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

支持向量机（Support Vector Machine，简称SVM）是一种强大而广泛应用的监督学习算法，用于分类和回归任务。本文将深入解析SVM的原理，从线性分类到核函数扩展

1. 线性分类与最大间隔

SVM的核心思想是在特征空间中找到一个最优的超平面，将不同类别的样本分开。对于线性可分的情况，SVM通过最大化分类边界（超平面）与两类样本之间的间隔来实现分类。这个间隔被称为最大间隔，使得SVM具有较好的鲁棒性和泛化能力

2. 支持向量

支持向量是指离最大间隔超平面最近的那些样本点。这些样本点对于定义超平面和决策边界起到重要作用。支持向量决定了SVM模型的结构和性能

3. 软间隔与惩罚因子

在实际应用中，很少有线性可分的数据集。为了处理线性不可分的情况，引入了软间隔（soft margin）概念。软间隔允许一些样本点位于超平面错误的一侧。为了平衡分类边界的鲁棒性和泛化能力，引入了惩罚因子C。C的取值决定了对误分类样本的容忍程度，较小的C会产生较宽松的决策边界，而较大的C会产生较严格的决策边界

4. 核函数扩展

当数据集不是线性可分的时候，线性SVM无法有效分类。为了解决这个问题，SVM引入了核函数的概念。核函数能够将低维特征空间中的样本映射到高维特征空间，从而使得原本线性不可分的问题变得线性可分。常用的核函数有线性核、多项式核、高斯核等

5. SVM的优缺点

SVM的优点：

可处理高维特征空间和样本数量较大的数据集
在处理线性可分问题时，具有较好的鲁棒性和泛化能力
支持不同核函数的扩展，能够处理非线性问题

SVM的缺点：

对于大规模数据集和高维数据集，训练时间较长
对于选择合适的核函数和参数调优较为敏感
在处理噪声较多的数据集时，容易产生过拟合

6. SVM代码示例

from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建SVM模型
model = SVC()

# 训练模型
model.fit(X_train, y_train)

# 预测结果
y_pred = model.predict(X_test)

# 评估模型
accuracy = accuracy_score(y_test, y_pred)
print("准确率：", accuracy)