用prim和kruskal算法求最小生成树问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了用prim和kruskal算法求最小生成树问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

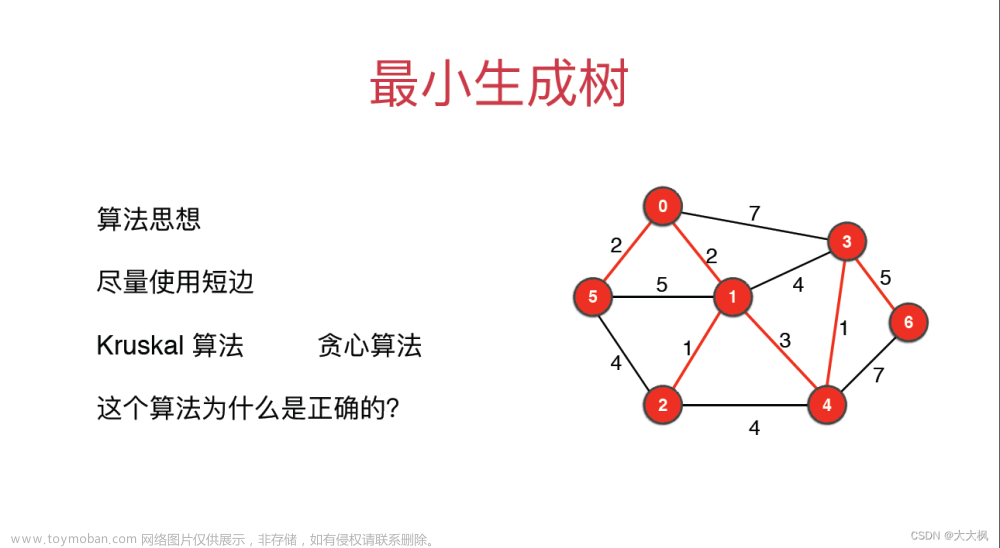
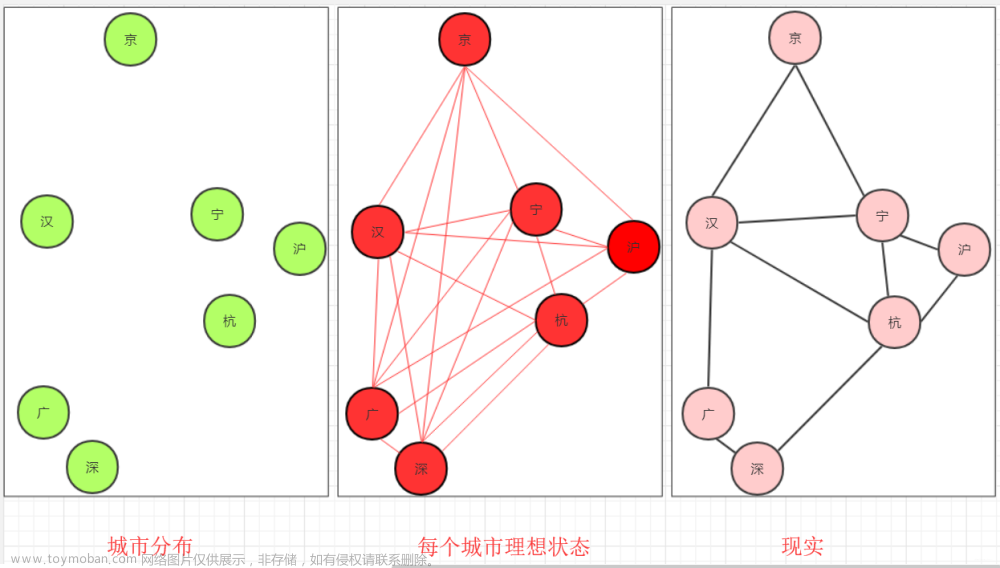
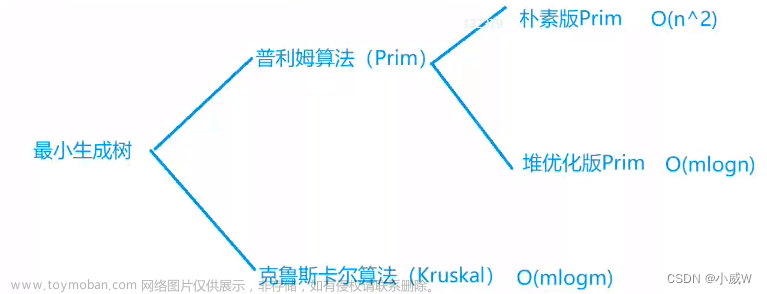
最短网络

题目http://ybt.ssoier.cn:8088/problem_show.php?pid=1350

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int w[N][N];
bool st[N];
int dist[N];
int n,res=0;
void prim()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;//初始化第一个点到自己的距离为0
    for(int i=1;i<=n;i++)//找剩下的n个点与第一起点的距离，就像dijkstra一样
    {
        int t=-1;
        for(int j=1;j<=n;j++)
            if(!st[j]&&(t==-1||dist[t]>dist[j]))//找不在连通块且距离最小的点
                 t=j;
        st[t]=true;//标记这个点在连通块内
        res+=dist[t];
        for(int j=1;j<=n;j++) dist[j]=min(dist[j],w[t][j]);//用该点更新其他点的最短距离
    }
}
int main()
{
   cin>>n;
   for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
         cin>>w[i][j];
   prim();
   cout<<res<<endl;
	return 0;
}

2.局域网

信息学奥赛一本通（C++版）在线评测系统 (ssoier.cn)http://ybt.ssoier.cn:8088/problem_show.php?pid=1391

相当于一个图中求最小生成树的问题

prim解决

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int w[N][N];
bool st[N];
int dist[N];
int n,res=0,m;
void prim()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;//初始化第一个点到自己的距离为0
    for(int i=1;i<=n;i++)//找剩下的n个点与第一起点的距离，就像dijkstra一样
    {
        int t=-1;
        for(int j=1;j<=n;j++)
            if(!st[j]&&(t==-1||dist[t]>dist[j]))//找不在连通块且距离最小的点
                 t=j;
        st[t]=true;//标记这个点在连通块内
        res+=dist[t];
        for(int j=1;j<=n;j++) dist[j]=min(dist[j],w[t][j]);//用该点更新其他点的最短距离
    }
}
int main()
{
    int ans=0;
   cin>>n>>m;
   memset(w,0x3f,sizeof w);
   while(m--)
   {
      int a,b,c;
      cin>>a>>b>>c;
      w[a][b]=w[b][a]=min(w[a][b],c);
      ans+=w[a][b];//记录所有网线的答案
   }
   prim();
   cout<<ans-res<<endl;//输出总的减最小生成数的
	return 0;
}

kruskal解法

#include<bits/stdc++.h>
using namespace std;
const int N=110,M=N*N;
int n,m;
struct Edge
{
    int a,b,w;
    bool operator < (const Edge&t)const//重载小于号，待会排序就按照w排序
    {
        return w<t.w;
    }
}e[M];//结构体存数
int p[N];
int find(int x)//并查集
{
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
int main()
{
   int ans=0;
   cin>>n>>m;
   for(int i=1;i<=n;i++) p[i]=i;//并查集初始化
   for(int i=0;i<m;i++)
   {
       int a,b,w;
       cin>>a>>b>>w;
       e[i]={a,b,w};
   }
   sort(e,e+m);//先排序
   for(int i=0;i<m;i++)
   {
       int a=find(e[i].a),b=find(e[i].b),w=e[i].w;
       if(a!=b) p[a]=b;//假如不在一个集合，则加上该条边
       else ans+=w;//反之该条边就是多余不要的加上答案里
   }
   cout<<ans<<endl;//输出总的减最小生成数的
	return 0;
}

3.繁忙的都市

信息学奥赛一本通（C++版）在线评测系统 (ssoier.cn)http://ybt.ssoier.cn:8088/problem_show.php?pid=1392

#include<bits/stdc++.h>
using namespace std;
const int N=310,M=N*N;
struct edge
{
	int a,b,c;
	bool operator < (const edge &t)const
	{
		return c<t.c;
	}
}e[M];
int n,m;
int p[N];
int res,maxx;
int find(int x)
{
	if(p[x]!=x)p[x]=find(p[x]);
	return p[x];
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)p[i]=i;
	for(int i=0;i<m;i++)
	{
		int a,b,c;
		cin>>a>>b>>c;
		e[i]={a,b,c};
	}
	sort(e,e+m);
	for(int i=0;i<m;i++)
	{
		int a=find(e[i].a),b=find(e[i].b),c=e[i].c;
		if(a!=b)
		{
			p[a]=b;
			res++;
			maxx=c;
		}
	}
	cout<<res<<" "<<maxx;
}

4.联络员

信息学奥赛一本通（C++版）在线评测系统 (ssoier.cn)http://ybt.ssoier.cn:8088/problem_show.php?pid=1393

#include<bits/stdc++.h>
using namespace std;
const int N=2010,M=N*N;
struct Edge
{
	int a,b,w;
	bool operator< (const Edge& t)
	{
		return w<t.w;
	}
}e[M];
int p[N];
int n,m;
int res;
int cnt;
int find(int x)
{
	if(p[x]!=x)p[x]=find(p[x]);
	return p[x];
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)p[i]=i;
	for(int i=0;i<m;i++)
	{
		int k,a,b,c;
		cin>>k>>a>>b>>c;
		if(k&1)
		{
			res+=c;
			p[find(a)]=find(b);
		}
		else 
		e[cnt++]={a,b,c};
	}
	sort(e,e+m);
	for(int i=0;i<m;i++)
	{
		int a=find(e[i].a),b=find(e[i].b),w=e[i].w;
		if(a!=b)
		{
			p[a]=b;
			res+=w;
		}
	}
	cout<<res<<endl;
}

5.连接格点

信息学奥赛一本通（C++版）在线评测系统 (ssoier.cn)http://ybt.ssoier.cn:8088/problem_show.php?pid=1394

就是给你已经连接了的点，让你加上某些边使他连通，也就是最小生成树，但是不能用prim，可能给出的边有环，只能用kruskal文章来源地址https://www.toymoban.com/news/detail-493349.html

#include<bits/stdc++.h>
using namespace std;
const int N=1010,M=N*N,K=2*M;
struct Edge
{
	int a,b,w;	
}e[K];
int p[M];
int id[N][N];
int n,m,cnt;

int find(int x)
{
	if(p[x]!=x)p[x]=find(p[x]);
	return p[x];
}
void edge()
{
    int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1},dw[4]={1,2,1,2};
    for(int s=0;s<2;s++)//s表示余数，0表示打横走，1表示纵着走
        for(int i=1;i<=n;i++)
          for(int j=1;j<=m;j++)
             for(int u=0;u<4;u++)
                if(u%2==s)//走的途径
               {
                    int x=i+dx[u],y=j+dy[u],w=dw[u];
                    if(x<=0||x>n||y<=0||y>m) continue;//假如越界
                    int a=id[i][j],b=id[x][y];//获取当前位置
                    if(a<b) e[cnt++]={a,b,w};//为了避免重复假如
               }
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n*m;i++)p[i]=i;
	for(int i=1,t=1;i<=n;i++)
	for(int j=1;j<=m;j++,t++)//映射坐标为点
	id[i][j]=t;
	int x1,x2,y1,y2;
	while(cin>>x1>>y1>>x2>>y2)
	{
		int a=id[x1][y1],b=id[x2][y2];
		p[find(a)]=find(b);//假如是连通块了，则加到同个连通块
	}
	edge();
	int res=0;
	for(int i=0;i<cnt;i++)
	{
		int a=find(e[i].a),b=find(e[i].b),w=e[i].w;
		if(a!=b)
		{
			p[a]=b;
			res+=w;
		}
	}
	cout<<res;
 }

到了这里，关于用prim和kruskal算法求最小生成树问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！