算法基础学习笔记——②二分-Toy模板网

这篇具有很好参考价值的文章主要介绍了算法基础学习笔记——②二分。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

✨博主：命运之光
✨专栏：算法基础学习

算法基础学习笔记——②二分

前言：算法学习笔记记录日常分享，需要的看哈O(∩_∩)O，感谢大家的支持！

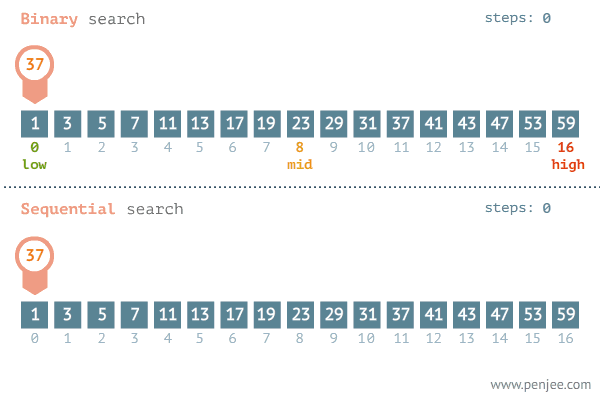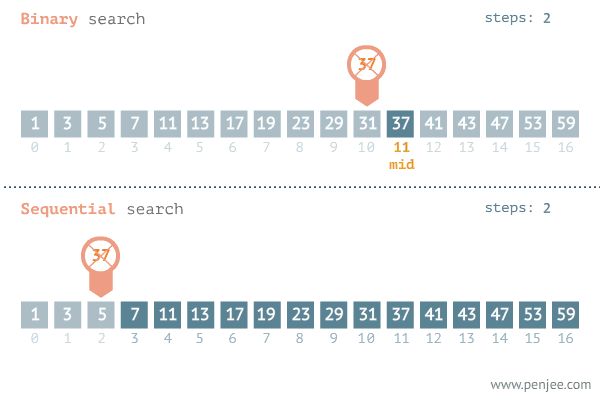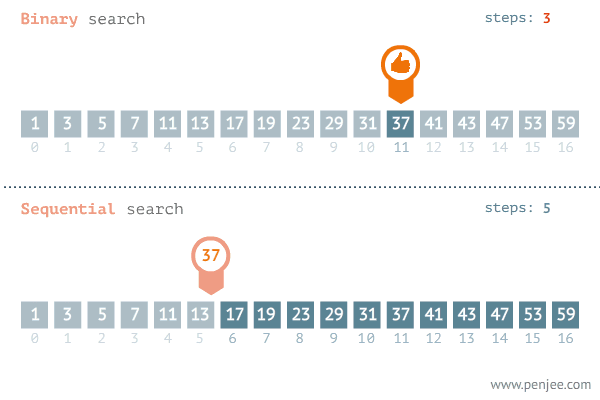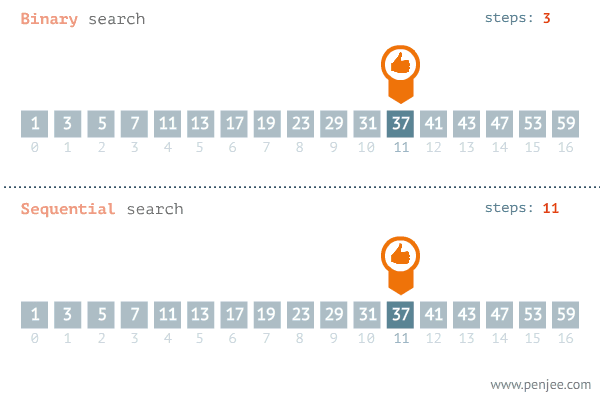
✨二分

🍓整数二分

1.有单调性一定可以二分，没有单调性也可能二分
2.二分的本质是边界，只要找到某种性质，使得整个区间一分为二，那么就可以用二分把整个边界点二分出来

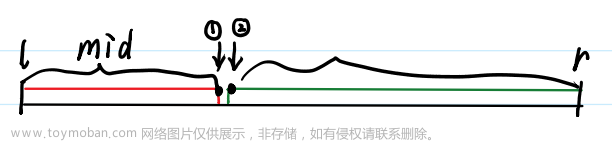
二分红色分界点时

解释这里为什么要+1：如果当l=r-1时, 不加1时mid=(l+r)/2=l(要下取整，1被略掉）,进行if(check(mid))如果为 true,则更新l=mid,可此时mid算出还是=l,故进入死循环）
此处check是否满足红色性质

区间[l, r]被划分成[l, mid -1]和[mid, r]时使用：

int bsearch_2(int l, int r){
    while (l < r)
        {
            int mid = l + r + 1 >> 1;
            if (check(mid)) l = mid;
            else r = mid -1;
        }
    return l;
}

此处check是否满足绿色性质

区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：

int bsearch_1(int l, int r){
	while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}

简单理解：mid的值不在所求答案区间（故找答案区间旁边的区间求mid的值）

🍓整数二分模板：

bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
	while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid -1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
	while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid -1;
    }
    return l;
}

//关于while的理解：
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
eg. 1 2 4 5 6 中查找3（答案没有）
每个数字的标号：0 1 2 3 4
第一次进入while循环：
mid=(0+4)/2=2,q[mid]=4;
If(q[mid]>=3)r=mid=2;
第二次进while循环：
mid=(0+2)/2=1,q[mid]=2;
if(q[mid]>=3)r=mid;
显然q[mid]❤️,
else l=mid+1=2;
现在l=r=2进入不了循环且q[l]!=3,（这里q[l]=q[r]就是最终二分彻底的值故没有找到3

🍓浮点数二分

当l～r足够小（≤[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-H8YrNrO8-1685067877207)(null#card=math&code=10^{-6}&id=a4G1L)]）就可以用l或r当作答案

🍓浮点数二分模板

bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
	while (r -l > eps)//写法2：for(int i=0;i<100;i++)   //不用精度，直接循环100次也可以
    {
        double mid = (l + r) / 2;//注意：这里不能写>>1,int时可进行>>1操作
        if (check(mid)) r = mid;
        else l = mid;
    } 
    return l;
}

小贴士：

🍓整数二分步骤：

1.找一个区间[L,R],使得答案一定在该区间中；
2.找一个判断条件，使得该判断条件具有二段性，并且答案一定是该二段性的分界点；
3.分析终点M在该判断条件下是否成立，如果成立，考虑答案在哪个区间：如果不成立，考虑答案在哪个区间；
4.如果更新方式写的是R=Mid,则不用做任何处理；如果更新方式写的是L=Mid,则需要在计算Mid时加上1。

遇见二分先画图文章来源地址https://www.toymoban.com/news/detail-493933.html

🍓二分模板2：

int 1=1,r=n,res;
while(1<=r)
{
    int mid=(1+r)/2;
    if(check(mid))
    {
        r=mid-1;
        res=mid;
    }
    else l=mid+1;
}
while(1<=r)
{
    int mid=(1+r)/2;
    if(check(mid))
    {
        1=mid+1;
        res=mid;
    }
    else r=mid-1;
}