LeetCode257. 二叉树的所有路径-Toy模板网

这篇具有很好参考价值的文章主要介绍了LeetCode257. 二叉树的所有路径。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

写在前面：

题目链接：LeetCode257. 二叉树的所有路径
题目难度：简单
编程语言：C++

一、题目描述

给你一个二叉树的根节点 root ，按任意顺序，返回所有从根节点到叶子节点的路径。

叶子节点是指没有子节点的节点。
LeetCode257. 二叉树的所有路径

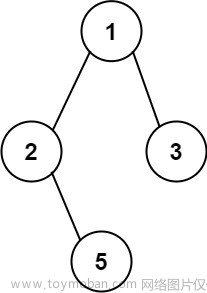
输入：root = [1,2,3,null,5]
输出：[“1->2->5”,“1->3”]

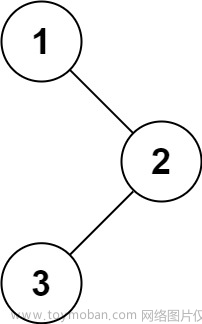
示例 2 ：

输入：root = [1]
输出：[“1”]

二、题目分析&解题思路

由于是从回溯法里找了一道题，那么就话不多说直接上回溯
如果之前没有了解过回溯的可以先看看回溯的思路：
LeetCode257. 二叉树的所有路径
如果还是不太理解的话，可以参考下面这篇博客：
LeetCode.46. 全排列(回溯法入门)

不过每个节点的值需要从 int 转到 string
刚开始不知道 C++ 里面有专门 Int To string 的方法(大傻子本人了)
然后自己啥没写，先自己手写了一个 Int To string 的方法，感觉太傻了，各位献丑了：

vector<string> vctMap = {"0","1","2","3","4","5","6","7","8","9"};
    string IntToStr(int val)
    {
        if(val >=0 && val < 10)
        {
            return vctMap[val];
        }
        else if(val>-10 && val <0)
        {
            val = -val;
            string strResult = "-" + vctMap[val];
            return strResult;
        }
        else 
        {
            bool isFushu = false;
            if(val < 0)
            {
                isFushu = true;
                val = -val;
            }
            //开始取每一位
            string strResult = "";
            while( val > 0)
            {
                int temp = val%10;
                strResult.insert(0,vctMap[temp]);
                val/=10;
            }
            if(isFushu)
            {
                strResult.insert(0, "-");
            }
            return strResult;
        }
    }

然后下面才是回溯的代码：

    //回溯函数
    void back(TreeNode* root, string strPath)
    {
        //终止条件
        if(root->left == nullptr && root->right == nullptr)
        {
            vctResult.push_back(strPath);
            return;
        }
        //不断向递归终止条件逼近
        //左
        if(root->left != nullptr)
        {
            string strTemp = "->"+IntToStr(root->left->val);
            strPath+=strTemp;
            back(root->left, strPath);
            //回溯 也就是把上一次的结果删除掉
            strPath.resize(strPath.size() - strTemp.size());
        }
        //右
        if(root->right != nullptr)
        {
            string strTemp = "->"+IntToStr(root->right->val);
            strPath+=strTemp;
            back(root->right, strPath);
            //回溯
            strPath.resize(strPath.size() - strTemp.size());
        }
        
    }

三、完整代码

class Solution {
public:
vector<string> vctResult;
string strPath = "";
vector<string> vctMap = {"0","1","2","3","4","5","6","7","8","9"};
public:
    //自己傻傻写的int to string 函数
    string IntToStr(int val)
    {
        if(val >=0 && val < 10)
        {
            return vctMap[val];
        }
        else if(val>-10 && val <0)
        {
            val = -val;
            string strResult = "-" + vctMap[val];
            return strResult;
        }
        else 
        {
            bool isFushu = false;
            if(val < 0)
            {
                isFushu = true;
                val = -val;
            }
            //开始取每一位
            string strResult = "";
            while( val > 0)
            {
                int temp = val%10;
                strResult.insert(0,vctMap[temp]);
                val/=10;
            }
            if(isFushu)
            {
                strResult.insert(0, "-");
            }
            return strResult;
        }
    }
    //回溯函数
    void back(TreeNode* root, string strPath)
    {
        //终止条件
        if(root->left == nullptr && root->right == nullptr)
        {
            vctResult.push_back(strPath);
            return;
        }
        //不断向递归终止条件逼近
        if(root->left != nullptr)
        {
        	//保存每个路径上的节点值
            string strTemp = "->"+IntToStr(root->left->val);
            strPath+=strTemp;
            back(root->left, strPath);
            //回溯
            strPath.resize(strPath.size() - strTemp.size());
        }
        if(root->right != nullptr)
        {
        	//保存每个路径上的节点值
            string strTemp = "->"+IntToStr(root->right->val);
            strPath+=strTemp;
            back(root->right, strPath);
            //回溯
            strPath.resize(strPath.size() - strTemp.size());
        }
        
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        if(root == nullptr)
        {
            return vctResult;
        }
        else
        {
            //先开始把根节点加上
            strPath = IntToStr(root->val);
            back(root, strPath);
            return vctResult;
        }

    }
};

运行结果：
LeetCode257. 二叉树的所有路径
我们再使用c++ 自己的to_string 接口试试：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
vector<string> vctResult;
string strPath = "";
public:
    //回溯函数
    void back(TreeNode* root, string strPath)
    {
        //终止条件
        if(root->left == nullptr && root->right == nullptr)
        {
            vctResult.push_back(strPath);
            return;
        }
        //不断向递归终止条件逼近
        //向左
        if(root->left != nullptr)
        {
            string strTemp = "->"+to_string(root->left->val);
            strPath+=strTemp;
            back(root->left, strPath);
            //回溯 也就是把上次的结果删除掉
            strPath.resize(strPath.size() - strTemp.size());
        }
        //向右
        if(root->right != nullptr)
        {
            string strTemp = "->"+to_string(root->right->val);
            strPath+=strTemp;
            back(root->right, strPath);
            //回溯
            strPath.resize(strPath.size() - strTemp.size());
        }
        
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        if(root == nullptr)
        {
            return vctResult;
        }
        else
        {
            //先开始把根节点加上
            strPath = to_string(root->val);
            back(root, strPath);
            return vctResult;
        }

    }
};