1.问题描述
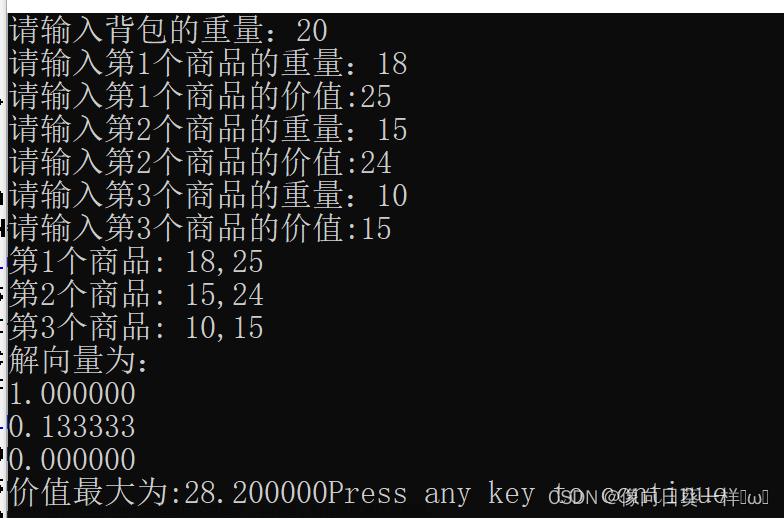
有一个容量为V的背包,还有n个物体。现在忽略物体实际几何形状,我们认为只要背包的剩余容量大于等于物体体积,那就可以装进背包里。每个物体都有两个属性,即体积w和价值v。使物品装入背包的价值最大。
2.解决思路与分析
I.枚举法,首先想到最简单的枚举法,通过列举所有结果,从中筛选出满足题意的结果。
II.回溯法,在枚举法的基础上进行约束剪枝和限界剪枝。
III.动态规划,运用动态规划思想,动态规划与分治法类似,都是把大问题拆分成小问题,通过寻找大问题与小问题的递推关系,使用递归和递推算法解决一个个小问题,最终达到解决原问题的效果。
如果装不下当前物品,那么前n个物品的最佳组合和前n-1个物品的最佳组合是一样的。
如果装得下当前物品。
假设1 :装当前物品,在给当前物品预留了相应空间的情况下,前n-1个物品的最佳组合加上当前物品的价值就是总价值。
假设2:不装当前物品,那么前n个物品的最佳组合和前n-1个物品的最佳组合是一样
选取假设1和假设2中较大的价值,为当前最佳组合的价值。
枚举法代码:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
const int N=10;//全局变量,物品数量
const int bag=N;//全局变量,背包承重量
int max_value=0;//全局变量,记录能获得的最大价值
int backpack(int a[],int v[],int w[],int n,int t)
{
int max_v=0,max_w=0;//背包累积的最大价值和最大重量
if(t>n-1)//递归结束的条件
{
printf("找到一个方案");
for(int i=0;i<n;i++){//遍历数组a根据其记录的0、1值进行背包价值和重量计算
printf("%d",a[i]);
max_v=max_v+v[i]*a[i];
max_w=max_w+w[i]*a[i];
}
if(max_w>bag)//根据max_w判断该方案是否超重
printf("\n该方案总价%d,总重%d,超重!不可行!!!\n",max_v,max_w);
else{//如果不超重
if(max_v>max_value)//比较该方案所获得的价值是不是比全局最优解更优
max_value=max_v;//更新最优解
printf("\n该方案总价%d,总重%d,可行\n",max_v,max_w);
}
}else{
for(int i=1;i>=0;i--)//只取值1或0
{
a[t]=i;//记录当前物品选1或不选0
backpack(a,v,w,n,t+1);//递归到下一层
}
}
return max_value;//返回最大价值
}
int main()
{
int a[N],v[N],w[N],i,start,end;
printf("背包最大承重%d公斤\n",bag);
for(i=0;i<N;i++)//随机生成价值和重量
{
v[i]=rand()%5+1;
w[i]=rand()%5+1;
printf("物品%d,价值%d,重量%d\n",i,v[i],w[i]);
}
start=clock();
printf("能获得的最大价值为:%d\n",backpack(a,v,w,N,0));
end=clock();
printf("耗时:%dms\n",end-start);
return 0;
}回溯法代码:文章来源:https://www.toymoban.com/news/detail-495252.html
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
const int N=10;//全局变量,物品数量
const int bag=N;//全局变量,背包承重量
int max_value=0;//全局变量,记录能获得的最大价值
int count=0;//全局变量,用于记录到达叶节点的次数
int a[N],v[N],w[N],r[N+1];//全局变量,分别保存0-1方案,物品价值,物品重量,剩余总价值
int backpack(int t,int now_v,int now_w)
{//t表示递归层数,now_v表示当前层所累积的价值,now_w表示当前层所累积的重量
int i;
if(t>N-1)//当递归到达叶子节点时
{
printf("找到一个方案");
for(i=0;i<N;i++)
{
printf("%d",a[i]);
}
if(now_w>bag)//判断方案是否超重
{
printf("\n该方案总价%d,总重%d,超重!不可行!!!\n",now_v,now_w);
}
else//如果不超重
{
if(now_v>max_value)//判断该方案所获得的价值是不是更优
{
max_value=now_v;//更新最优解
}
printf("\n该方案总价%d,总重%d,可行\n",now_v,now_w);
}
count++;
}
else
{
for(i=0;i<=1;i++)
{
a[t]=i;//记录当前物品选或不选
now_v=now_v+v[t]*i;//根据0-1值累加价值
now_w=now_w+w[t]*i;//根据0-1值累加重量
if(now_w<=bag&&now_v+r[t+1]>max_value) // (限件减枝 约束减枝)
backpack(t+1,now_v,now_w);//递归到下一层
}
}
return max_value;//返回最大价值
}
int main()
{
int i,start,end;
printf("背包最大承重%d公斤\n",bag);
for(i=0;i<N;i++)//随机生成价值和重量范围1-5
{
v[i]=rand()%5+1;
w[i]=rand()%5+1;
printf("物品%d,价值%d,重量%d\n",i,v[i],w[i]);
}
r[N]=0;
for(i=N-1;i>=0;i--)//计算所有情况下剩余物品的总价值(约束减枝)
{
r[i]=r[i+1]+v[i];
}
start=clock();
printf("能获得的最大价值为:%d\n",backpack(0,0,0));
end=clock();
printf("检查方案%d个,",count);
printf("耗时:%dms\n",end-start);
return 0;
}动态规划代码:文章来源地址https://www.toymoban.com/news/detail-495252.html
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
const int N=1000;//全局变量,物品数量
const int bag=N;//全局变量,背包承重量
int max_value=0;//全局变量,记录能获得的最大价值
int a[N],v[N],w[N],r[N+1];//全局变量,分别保存0-1方案,物品价值,物品重量,剩余总价值
int dp[N][bag+1]={0},fa[N]={0};
int max(int a,int b);
void Find(int N,int bag);
int backpack()
{
for(int i=1;i<N;i++)
{
for(int j=1;j<=bag;j++)
{
if(w[i]>j)
dp[i][j]=dp[i-1][j];
else
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
}
}
return dp[N-1][bag];//返回最大价值
}
void Find(int i,int j)
{
if(i==0)
{
for(int i=0;i<N;i++)
printf("%d",fa[i]);
}
if(dp[i][j]==dp[i-1][j])
{
fa[i]=0;
Find(i-1,j);
}
else if(dp[i][j]==dp[i-1][j-w[i]]+v[i])
{
fa[i]=1;
Find(i-1,j-w[i]);
}
}
int main()
{
int i,start,end;
printf("背包最大承重%d公斤\n",bag);
for(i=0;i<N;i++)//随机生成价值和重量范围1-5
{
v[i]=rand()%5+1;
w[i]=rand()%5+1;
printf("物品%d,价值%d,重量%d\n",i,v[i],w[i]);
}
r[N]=0;
start=clock();
printf("能获得的最大价值为:%d\n",backpack());
end=clock();
Find(N-1,bag-1);
printf("耗时:%dms\n",end-start);
return 0;
}
int max(int a,int b)
{
if(a>b) return a;
else return b;
}到了这里,关于0-1背包问题的多种算法求解(C语言)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!