matlab基础知识加矩阵运算初步-Toy模板网

这篇具有很好参考价值的文章主要介绍了matlab基础知识加矩阵运算初步。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

** matlab（matrix laboratory）**

功能符号

1.分号（;）

不让matlab显示运算结果，抑制输出

2.续行号(…)

某行命令太长,指令行必须多行书写时，使用“…"处理，表示下一行是上一行的连续

常用指令

1.cd

显示或改变工作目录

2.clc

清空命令行窗口

3.clear

清除所有变量

clear+变量名清除一个特定的变量

clear+ 变量名1 变量名2（用空格分隔名称）

4.其他命令

disp 显示变量或文字内容

radius=5;
area=pi*radius^2;
disp(["the area of the disc is " area]);
>>"the area of the disc is"    "78.5398"

radius = 5;
area=pi*radius^2;
disp(['the area of the disc is ' area]);
>>the area of the disc is N

radius = 5;
area=pi*radius^2;
disp(['the area of the disc is ' num2str(area)]);
>>the area of the disc is 78.5398

变量与常量

变量

1.以字母开头，之后可以包含字母，数字，下划线
2.namelengthmax 最大名称长度=63
3.区分大小写
4.保留词关键词不能用作变量名
5.内置函数的名称不能用作变量名
6.who显示了在命令行窗口定义的变量
7.whos显示了在命令行窗口定义的变量的更多信息

常量

i(j) 复数中的虚数单位，前面可以加任意实数
inf 向上取极限+∞
pi 圆周率
eps 浮点运算相对精度
NaN 代表“不是一个数字”

格式功能

format rat 使用分数来表示数值
format bank 控制小数点后2位
format short 控制小数点后4位
format long 控制小数点后15位

>>format short                       >>format long 
>>pi                                 >>pi

ans =                                ans =

    3.1416                                3.141592653589793

格式命令还可以用于控制matlab命令与表达式的间距，可以是松散的（默认）或紧凑的
‘>>format loose’

‘>>format compact’

内置函数功能

help elfun
将显示很长的列表，分为三角函数，指数函数，复函数，舍入和剩余函数
sin+弧度
sind+角度
fix：向0取整
floor:向-∞取整
ceil：向+∞取整
round：四舍五入
`round(pi,2)保留2位小数
abs：绝对值
rem：返回除法的余数

rem(13,5)  
>>ans=3
fix(19.999)
>>ans=19

mod(5,0)=5
rem(5,0)=NaN
sign 符号函数
nthroot(x,n):返回x元素的n次方实根
deg2rad:角的单位从度转换为弧度
rad2deg:角的单位从弧度转换为角度
log( ) :以e为底数
log2( ):以2为底
exp(n):e的n次方
查看ceil功能
1>>help ceil
2.ce[光标]il+F1
3.搜索

随机数

rng重置
rng(seed)改变初始种子
seed为小于 2^32 的非负整数种子。
rng(seed)=rng([seed])
rng(‘default’) 恢复matlab启动时默认的全局随机流
rng(‘shuffle’)* 根据当前时间为随机数生成器提供种子
rand 0-1的均匀随机分布，包括0和1
rand(m,n)产生m行n列的矩阵

 R = rand(N)              % 生成N×N的矩阵随机数，其中每个元素位于0~1之间，故N必须为整数
 R = rand([M,N,P,...])    % 生成M×N×P×...的矩阵随机数
 R = rand(M,N,P,...)      % 同上，中括号不是必须
 R = rand(..., CLASSNAME) % 生成CLASSNAME类型的随机数，如 'double' or 'single'

rand的应用实例

>> rand
ans =
    0.7060
>> rand()
ans =
    0.0318
>> rand(1)
ans =
    0.2769
>> rand(2)
ans =
    0.0462    0.8235
    0.0971    0.6948
>> rand([3,2,2])
ans(:,:,1) =
    0.3171    0.4387
    0.9502    0.3816
    0.0344    0.7655
ans(:,:,2) =
    0.7952    0.4456
    0.1869    0.6463
    0.4898    0.7094

randn 均值为0方差为1的正态分布
randn(m,n)产生m行n列的矩阵
randi
randi(N) 是生成(0,N]间均匀分布的伪随机数，并且数都是整数，所以括号中每个数是位于1到N之间
randi(n)不超过n的1个正整数
randi([1,12]) 在[1,12]直接产生一个正整数
randi(1,12)产生一个12行12列全为1的矩阵

R = randi(iMax)            % 生成1：iMax之间的均匀分布随机数
R = randi(iMax,m,n)        % 生成m×n的1：iMax之间的均匀分布随机数
R = randi([iMin,iMax],m,n) % 生成m×n的iMin:iMax之间的均匀分布随机数
R = randi([iMin,iMax],[m,n]) %  同上，中括号不是必须

用round生成m行n列随机整数矩阵
round(rand(m,n)* 10)
把0-10之间的小数四舍五入取整数得到0~10之间的整数，包括0和10
round(rand(m,n)* 10,n)
把0-10之间的小数四舍五入取n位小数得到0~10之间的整数
matlab基础知识加矩阵运算初步

找以···开头的函数

randn(m,n)可以通过回溯command history
操作方式：
函数开头几个字母+↑(方向键上键)

Tab 自动补全

随机数生成器并不是真正随机，它的工作方式是从一个数字开始，这个数字通常被称为种子，通常初始种子是预定值，或者从计算机中内置时钟中获得，基于种子通过一个过程确定下一个随机数，下一次使用这个数字作为种子，生成另一个随机数，下一次使用这个数字作为种子，生成另一个随机数，以上过程称为伪随机

数值类型

single4字节，double8字节
matlab基础知识加矩阵运算初步

数值范围

matlab基础知识加矩阵运算初步

>>intmax('int16')               >> intmin('int16')
    ans=                              ans=                                  
    int16                             int16
     32767                             -32768
   %2^16/2-1                         %-2^16/2
>>intmax('uint8')                 >>intmin('uint8')
 ans=                               ans=                                
  uint8                             uint8
   255                               0
%2^8-1                         

>>int8(200)                       >>int8(200)
ans=                              ans=                                
 int8                             int 8
  127                              -128
%saturation饱和
>>double('程序设计')
 ans=
  31243 24207 35574 35745
>>realmax('double')
ans =
    1.797693134862316e+308
>> double(3E308)                 >>double(-3E308)
ans =                             ans =
   Inf                            -Inf
%舍入误差的影响
%由于计算机中用有限位数的浮点数存储实数，导致存储值与真实值存在差异，这便是舍入误差。
>>abs((0.001+1E0-1E0)-0.001)
ans =
     1.101549407245273e-16
>>abs((0.001+1E0-1E0)-0.001)<1E-13
ans=
   logical
    1

逻辑运算符

&&或&或and 逻辑与
| 或||或or 逻辑或
~或not 逻辑非
xor 逻辑异或，有且只有1个正确返回1
any 有非零元素即为1
all 所有元素均非零则为1

>> vec=[5 9 3 4 6 11]
vec =
     5     9     3     4     6    11
>> v=[0 1 0 0 1 1]
v =
     0     1     0     0     1     1
>> v=logical([0 1 0 0 1 1])
v =
  1×6 logical 数组
   0   1   0   0   1   1
>> vec(v)
ans =
     9     6    11
>> any(v)
ans =
  logical
   1
>> all(v)
ans =
  logical
   0
 >> xor('c'=='d'-1,2<4)
 ans =
  logical
   0

运算优先级

matlab基础知识加矩阵运算初步

创建行向量

1.直接输入法

>> v=[1 2 3 4]
v =
 1     2     3     4

2.冒号法

本实例创建一个从3开始，增量为1，到9结束的行向量v

>> v=[3:1:9]
v =
  3     4     5     6     7     8     9

当中间的增量省略时，默认增量为1

>> v=(1.5:8.7)                                      %也可以不加括号
v =
 1.5000    2.5000    3.5000    4.5000    5.5000    6.5000    7.5000    8.5000 >> v=(1.5:8.7)
v =
 1.5000    2.5000    3.5000    4.5000    5.5000    6.5000    7.5000    8.5000

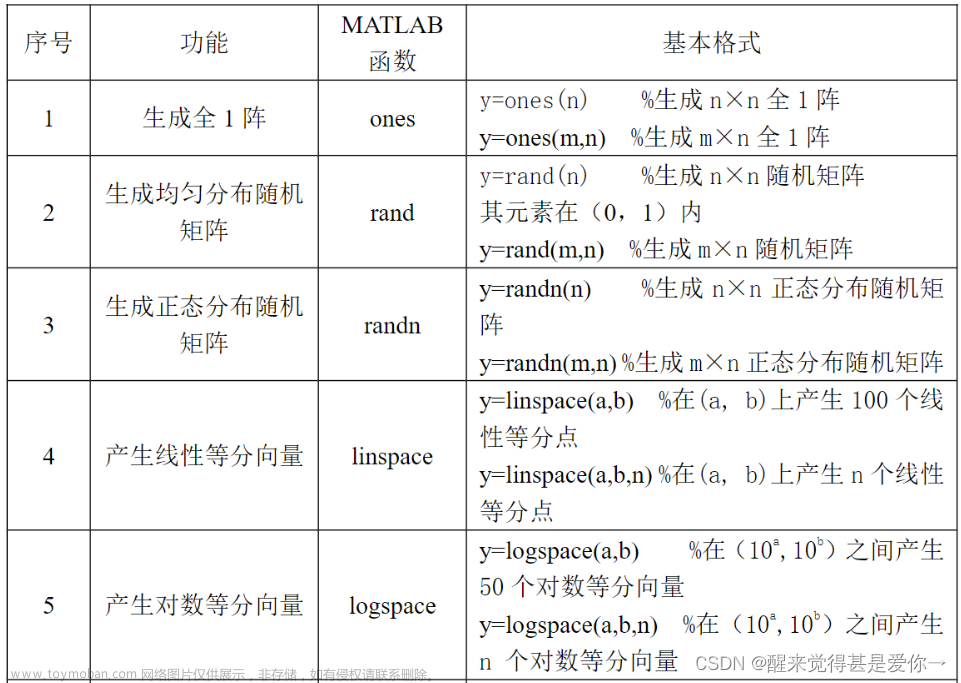
3.利用函数linspace()创建向量

lincpace(first_value,last_value,number)
该调用格式表示创建一个从first_value开始，到last_value结束,包含number个元素的向量

>> linspace(3,9,7)
ans =
   3     4     5     6     7     8     9

4.利用函数logspace()创建一个对数分隔的向量

logspace(first_value,last_value,number)
![[Pasted image 20230110115606.png]]

>>x=logspace(1,3,3)
x=
   10    100     1000

5.拼接行向量

>> v=(3:9)
v =
   3     4     5     6     7     8     9
>> u=0.1:0.2:0.9
u =
   0.1000    0.3000    0.5000    0.7000    0.9000
>> [u,v]
ans =
   0.1000    0.3000    0.5000    0.7000    0.9000    3.0000    4.0000    5.0000    6.0000    7.0000    8.0000    9.0000

工作区u右键打开所选内容
matlab基础知识加矩阵运算初步

6.添加一个元素

>> v=3:9
v =
     3     4     5     6     7     8     9
>> v(10)=12
v =
     3     4     5     6     7     8     9     0     0    12

7.替换一个元素

>> v=3:9
v =
     3     4     5     6     7     8     9
>> v(2)=15
v =
     3    15     5     6     7     8     9

8.查找一个元素

>> v=(3:9)
v =
     3     4     5     6     7     8     9
>> v(3)
ans =
     5
>> v([3,5])
ans =
     5     7
>> v([3:5])
ans =
     5     6     7
>> v(end)
ans =
     9

9.向量转置

>> v=(3:9)'
v =
     3
     4
     5
     6
     7
     8
     9

创建列向量

>> [3;7;4]
ans =
     3
     7
     4

矩阵转置

>> [3,7,4]'
ans =
     3
     7
     4            %是共轭转置

共轭转置(')

>> [1+3i,2-7i,5+4i]'
ans =
   1.0000 - 3.0000i
   2.0000 + 7.0000i
   5.0000 - 4.0000i

转置(.')

>> [1+3i,2-7i,5+4i].'
ans =
   1.0000 + 3.0000i
   2.0000 - 7.0000i
   5.0000 + 4.0000i

创建矩阵

>> mat=[4,3,1;2,5,6]
mat =
     4     3     1
     2     5     6
>> lab=[2:4;3:5]
lab =
     2     3     4
     3     4     5

创建特殊矩阵

zeros(n):创建n×n全0矩阵
zeros(m,n):创建m×n全0矩阵
ones(n):创建n×n全1矩阵
ones(m,n):创建m×n全1矩阵
eye(n):创建n×n单位矩阵
eye(m,n):创建m×n的单位矩阵
单位矩阵：主对角线元素为1，其余元素为0的矩阵
hilb(n):创建n×n的希尔伯特矩阵
magic(n)生成n阶魔方矩阵
魔方矩阵：是有相同的行数和列数，并在每行每列、对角线上的和都相等的矩阵
pascal矩阵：
matlab基础知识加矩阵运算初步

>> format rat
>> hilb(5)
ans =
       1              1/2            1/3            1/4            1/5     
       1/2            1/3            1/4            1/5            1/6     
       1/3            1/4            1/5            1/6            1/7     
       1/4            1/5            1/6            1/7            1/8     
       1/5            1/6            1/7            1/8            1/9

矩阵的抽取

diag(v):创建以向量v中的元素为对角的对角阵
对角阵：只有对角线上有非0元素的矩阵称为对角矩阵

>> v=3:9
v =
     3     4     5     6     7     8     9
>> diag(v)
ans =
     3     0     0     0     0     0     0
     0     4     0     0     0     0     0
     0     0     5     0     0     0     0
     0     0     0     6     0     0     0
     0     0     0     0     7     0     0
     0     0     0     0     0     8     0
     0     0     0     0     0     0     9

diag(v,k)得到矩阵 v 对角线上移k行的元素组成的列向量，diag(v,-k)得到矩阵 v 对角线下移k行的元素组成的列向量。

v=[1 2 3];
diag(v, -1)
ans =
      0 0 0 0
      1 0 0 0
      0 2 0 0
      0 0 3 0
      
>> diag(-1:-1:-6,-1)+diag(v)
ans =
     3     0     0     0     0     0     0
    -1     4     0     0     0     0     0
     0    -2     5     0     0     0     0
     0     0    -3     6     0     0     0
     0     0     0    -4     7     0     0
     0     0     0     0    -5     8     0
     0     0     0     0     0    -6     9

diag(X):抽取主对角线
diag(X,k):抽取矩阵X的第k条对角线上的元素向量。k为0时抽主对角线,k为正整数时抽取上方第k条对角线上的元素，k为负整数时抽取下方第k条对角线上的元素

>> X=randi([1,9],[5,5])
X =
     8     1     2     2     6
     9     3     9     4     1
     2     5     9     9     8
     9     9     5     8     9
     6     9     8     9     7
>> diag(X,-1)
ans =
     9
     5
     5
     9

tril(X):提取矩阵X的主下三角部分
tril(X,k):提取矩阵第k条对角线下面的部分(包括第k条对角线)
triu(X):提取矩阵X的主上三角部分
triu(X,k):提取矩阵第k条对角线上面的部分(包括第k条对角线)

>> tril(X,-1)
ans =
     0     0     0     0     0
     9     0     0     0     0
     2     5     0     0     0
     9     9     5     0     0
     6     9     8     9     0

访问矩阵

>> M=[9,6,3;5,7,2]
M =
     9     6     3
     5     7     2
>> M(2,3)
ans =
     2
>> M(2,[1,3])
ans =
     5     2
>> M(1,1:3)
ans =
     9     6     3
>> M(1,:)                    %表示第一行
ans =
     9     6     3
>> M(:,2)                    %表示第二列
ans =
     6
     7
>> M(:,end)                 %表示最后一列
ans =
     3
     2

矩阵的变维

reshape是对矩阵的元素重新排列的方法

>> M=randi([1,9],[3,4])
M =
    9     6     3     8
    8     6     5     2
    5     2     3     3
>> reshape(M,2,6)
ans =
    9     5     6     3     3     2
    8     6     2     5     8     3
    M=randi([1,9],[3,4])
M =
    9     6     3     8
    8     6     5     2
    5     2     3     3
>> reshape(M,2,6)
ans =
    9     5     6     3     3     2
    8     6     2     5     8     3
>> M(2)                               %查找元素
ans =
    8
>> M([6 2 5 4])                      
ans =
2     8     6     6

matlab基础知识加矩阵运算初步

>> A=1:12
A =
     1     2     3     4     5     6     7     8     9    10    11    12
>> C=zeros(3,4);
>> C(:)=A(:)
C =
     1     4     7    10
     2     5     8    11
     3     6     9    12

修改矩阵元素

matlab基础知识加矩阵运算初步

扩充矩阵

>> M=[9,6,3;5,7,2]
M =
     9     6     3
     5     7     2
>> N=[M;10 11 12]
N =
     9     6     3
     5     7     2
    10    11    12
>> M=[9,6,3;5,7,2]
M =
     9     6     3
     5     7     2
>> M(1:2,1:2)=[7,8;9,10]    %1~2行和1~2列的交集子矩阵
   %1~2行%1~2列  
M =
     7     8     3
     9    10     2
>> M(1:2,1:2)=[7,8,9,10]
无法执行赋值，因为左侧的大小为 2-by-2，右侧的大小为 1-by-4。 
**更改一个矩阵的二维子集左右两边形状要相同**
>> M=[9,6,3,1;5,7,2,8;3,2,1,9]
M =
     9     6     3     1
     5     7     2     8
     3     2     1     9
>> M(1:2,1:3)=[7,8,9;10,4,5]
M =
     7     8     9     1
    10     4     5     8
     3     2     1     9
>> M(1,:)=0.5
M =
    0.5000    0.5000    0.5000    0.5000
   10.0000    4.0000    5.0000    8.0000
    3.0000    2.0000    1.0000    9.0000
>> M(1:2,1:2)=Inf
M =
       Inf       Inf    0.5000    0.5000
       Inf       Inf    5.0000    8.0000
    3.0000    2.0000    1.0000    9.0000
 >> M(end-1,:)
ans =
   Inf   Inf     5     8

矩阵的变向

fliplr(X):将X左右翻转
flipud(X):将X上下翻转
flip(X):同上，将X上下翻转，以及将一个行向量左右翻转，列向量上下翻转

>> X=randi([1,9],[3,4])
X =
     3     4     8     5
     9     4     2     6
     1     7     5     7
>> flipud(X)
ans =
     1     7     5     7
     9     4     2     6
     3     4     8     5
>> flip(X)
ans =
     1     7     5     7
     9     4     2     6
     3     4     8     5

rot90(X):将X逆时针方向旋转90°

>> X=randi([1,9],[3,4])
X =
     7     6     5     6
     3     2     9     3
     7     2     4     7
>> rot90(X)
ans =
     6     3     7
     5     9     4
     6     2     2
     7     3     7

向量和矩阵的常用函数

1.length(M):返回M矩阵行数和列数的较大值
2.size(M):返回M矩阵的行数和列数
3.numel(M):返回M矩阵中元素的个数

>> length(M)
ans =
     3
>> size(M)
ans =
     2     3
>> [n_row,n_col]=size(M)
n_row =
     2
n_col =
     3
>> numel(M)
ans =
     6

3.repmat()

创建一个矩阵，并将原矩阵(或元素或字符串)复制到新矩阵块中

使用相同的元素值初始化矩阵

创建一个所有元素的值均为 10 的 3×2 矩阵。
A = repmat(10,3,2)

垂直行向量堆栈

垂直堆叠行向量四次。

>>A = 1:4;
>>B = repmat(A,4,1)
B = 4×4

     1     2     3     4
     1     2     3     4
     1     2     3     4
     1     2     3     4

包含列向量的水平堆栈

A = (1:3)';  
B = repmat(A,1,4)
B =
     1     1     1     1
     2     2     2     2
     3     3     3     3

方块格式

>> A=[1 2;3 4]
A =
     1     2
     3     4
>> B=repmat(A,2)
B =
     1     2     1     2
     3     4     3     4
     1     2     1     2
     3     4     3     4

矩形块格式

>> repmat(A,2,3)
ans =
     1     2     1     2     1     2
     3     4     3     4     3     4
     1     2     1     2     1     2
     3     4     3     4     3     4

三维块数组

B = repmat(A,[2 3 2])

B = 
B(:,:,1) =

     1     2     1     2     1     2
     3     4     3     4     3     4
     1     2     1     2     1     2
     3     4     3     4     3     4


B(:,:,2) =

     1     2     1     2     1     2
     3     4     3     4     3     4
     1     2     1     2     1     2
     3     4     3     4     3     4

4.repelem()函数

创建一个矩阵，将每个元素复制到一个新矩阵块中
repelem作为两输入函数使用，第二个参数如果是一个数值，第一个参数要么是单个数值，要么是向量，不能是矩阵，第二个参数也为向量时，两个向量必须等长

>>repelem(3,5)
ans=
  3 3 3 3 3
>> repelem([1,2,3],3)
ans =
     1     1     1     2     2     2     3     3     3
>> repelem([1;2;3],3)
ans =
     1
     1
     1
     2
     2
     2
     3
     3
     3
>> repelem([1,2,3],[3,2,1])  
ans =
     1     1     1     2     2     3

当repelem接受两个以上参数时，第一个参数为高维数组，后面有维数个参量，分别控制每一维度的重复。

如图，repelem([1,2;3,4],3,2)是将矩阵[1,2;3,4]沿着第一维重复3次，沿着第二维重复2次。

>>  A=[1 2;3 4]
A =
     1     2
     3     4
>> B=repelem(A,3,2)
B =
     1     1     2     2
     1     1     2     2
     1     1     2     2
     3     3     4     4
     3     3     4     4
     3     3     4     4

当然，每一维度的对应参数可以是和那一维度长度相等的向量。如图，沿着第一维重复4个,2个,沿着第二维重复3个,1个

>> repelem([1,2;3,4],[4,2],[3,1])
ans =
     1     1     1     2
     1     1     1     2
     1     1     1     2
     1     1     1     2
     3     3     3     4
     3     3     3     4
     A = [1 2; 3 4]
A = 2×2
 
     1     2
     3     4
 
B = repelem(A,1,[2 3])
B = 2×5
 
     1     1     2     2     2
     3     3     4     4     4

三维数组

M=randi([1,9],[3,4])

M =

     9     7     1     8
     3     4     1     9
     7     6     5     2

>> T(:,:,1)=M

T =

     9     7     1     8
     3     4     1     9
     7     6     5     2

>> T(:,:,2)=randi([1,9],[3,4])

T(:,:,1) =

     9     7     1     8
     3     4     1     9
     7     6     5     2


T(:,:,2) =

     6     4     3     6
     5     2     5     3
     1     8     2     6

>> T(:,:,3)=randi([1,9],[3,4])

T(:,:,1) =

     9     7     1     8
     3     4     1     9
     7     6     5     2


T(:,:,2) =

     6     4     3     6
     5     2     5     3
     1     8     2     6


T(:,:,3) =

     7     1     2     9
     7     3     8     1
     5     9     5     4

>> T(:,:,4)=randi([1,9],[3,4])

T(:,:,1) =

     9     7     1     8
     3     4     1     9
     7     6     5     2


T(:,:,2) =

     6     4     3     6
     5     2     5     3
     1     8     2     6


T(:,:,3) =

     7     1     2     9
     7     3     8     1
     5     9     5     4


T(:,:,4) =

     1     7     1     8
     9     8     4     4
     1     8     3     9

>> T(:,:,5)=randi([1,9],[3,4])

T(:,:,1) =

     9     7     1     8
     3     4     1     9
     7     6     5     2


T(:,:,2) =

     6     4     3     6
     5     2     5     3
     1     8     2     6


T(:,:,3) =

     7     1     2     9
     7     3     8     1
     5     9     5     4


T(:,:,4) =

     1     7     1     8
     9     8     4     4
     1     8     3     9


T(:,:,5) =

     2     2     5     6
     3     8     2     4
     2     6     8     5

>> size(T)

ans =

     3     4     5

>> whos
  Name      Size             Bytes  Class     Attributes

  A         2x2                 32  double              
  E         0x0                  0  double              
  M         3x4                 96  double              
  T         3x4x5              480  double              
  ans       1x3                 24  double   
  >> numel(T)

ans =

    60

数组中的常用其他函数

函数在向量中的应用

>> a=[-3,-3,2,9,0]
a =
    -3    -3     2     9     0
>> max(a)
ans =
     9
>> min(a)
ans =
    -3
>> sum(a)
ans =
     5
>> prod(a)
ans =
     0
>> cumsum(a)
ans =
    -3    -6    -4     5     5
>> cummin(a)
ans =
    -3    -3    -3    -3    -3
>> cummax(a)
ans =
    -3    -3     2     9     9
>> cumprod(a)
ans =
    -3     9    18   162     0

函数在矩阵中的应用

>> M=randi([1,9],[3,4])
M =
     6     4     1     7
     1     8     2     6
     3     1     6     5
>> min(M)        %返回每一列的最小值
ans =
     1     1     1     5
>> max(M)        %返回每一列的最大值
ans =
     6     8     6     7
>> sum(M)        %返回每一列各个数的和
ans =
    10    13     9    18
>> prod(M)       %返回每一列各个数的乘积
ans =
    18    32    12   210
>> cummin(M)     %返回每一列第一个元素最小值，前两个元素最小值，前三个
ans =                %元素最小值
     6     4     1     7
     1     4     1     6
     1     1     1     5
>> cummax(M)      %返回每一列第一个元素最大值，前两个元素最大值，前三个
ans =                %元素最大值
     6     4     1     7
     6     8     2     7
     6     8     6     7
>> cumsum(M)       %返回每一列第一个元素，第一个和第二个元素的和，前三个元素的和
ans =
     6     4     1     7
     7    12     3    13
    10    13     9    18
>> cumprod(M)     %返回每一列第一个元素，第一个第一个和第二个元素的乘积，前三个元素的乘积
ans =
     6     4     1     7
     6    32     2    42
    18    32    12   210

matlab中cumsum函数的使用

A =
     1     2     3
     4     5     6
     7     8     9
>>B=cumsum(A)
B =                                                                      
     1     2     3
     5     7     9                
    12    15    18

matlab基础知识加矩阵运算初步

A =
     1     2     3  
     4     5     6  
     7     8     9
>> B=cumsum(A,1)
B =
     1     2     3
     5     7     9
    12    15    18
>> B=cumsum(A,2)
B =
     1     3     6
     4     9    15
     7    15    24

diff()函数：求差距

>> diff([1 4 7 8 3])
ans =
     3     3     1    -5

logical数组索引

>> w=[5 9 3 4 6 11]
w =
     5     9     3     4     6    11
>> v=[0 1 0 0 1 1]
v =
     0     1     0     0     1     1
>> w(v)
数组索引必须为正整数或逻辑值。 
>> v=logical([0 1 0 0 1 1])
v =
  1×6 logical 数组
   0   1   0   0   1   1
>> w(v)
ans =
     9     6    11

find():返回逻辑真元素的位置

>> d=[0 1 0 0 1]
d =
       0              1              0              0              1       
>> find(d)
ans =
       2              5       
>> find(d,1,'first')
ans =
       2       
>> find(d,2,'first')
ans =
       2              5       
>>vec=[11 -5 33 2 8 -4 25]   %寻找大于0的元素的方法
vec =
      11          -5           33           2           8          -4          25       
>> vec=vec(find(vec>0))
vec =
      11             33              2              8             25       
>> vec(vec>0)
ans =
      11             33              2              8             25  
%下面寻找0和1之间发生变化多少次
>> v=randi([0,1],[1,100]);
>> sum(diff(v)==1)     %0->1
ans =
      23       
>> sum(diff(v)==-1)   %1->0
ans =
      23     
%下面寻找发生1->2的变化多少次，提供两种方法
①
>> U=randi([0,2],[1,1000]);
>> U(1:10)
ans =
     1     2     0     2     0     1     1     0     2     1
>> U2=U;
>> U2(U2==0)=NaN;
>> U2(1:10)
ans =
     1     2   NaN     2   NaN     1     1   NaN     2     1
>> sum(diff(U2)==1)
ans =
       122
②
>> U3=U(1:10)
U3 =
     1     2     0     2     0     1     1     0     2     1
>> V1=U(1:end-1);
>> V2=U(2:end);
>> sum(V1==1&V2==2)
ans =
	   122
>> M=randi([1,9],[4,4])
M =
     5     1     5     7
     8     5     3     9
     1     7     6     1
     8     6     9     5
>> [I J] = find(M == 1)%或者[I,J]=ind2sub(size(M),find(M==1))
>> I =
     3
     1
     3
J =
     1
     2
     4

isequal(v1,v2···vn) 判断矩阵是否完全相同
不仅对应数字要相等，维度也要一致

矩阵运算

M1* M2 两矩阵相乘

M0= 
   4  8  8  3
   9  3  6  3
   1  9  8  6
   6  7  3  8
M0*M0=M0^2
ans=114  149  153  108
    
     87  156  147   96
    
    129  149  144  126
    
    138  152  138  121
>>M0.^2
ans=
    16   64   64    9

    81    9   36    9

     1   81   64    36

    36   49    9    64

两向量相乘文章来源地址https://www.toymoban.com/news/detail-495534.html

>> v1=randi([1 9],[1 3])
v1 =
     2     3     1
>> v2=randi([1 9],[1 3])
v2 =
     7     1     6
>> v1.*v2
ans =
    14     3     6
>> sum(v1.*v2)
ans =
    23
v1*v2'
>>ans =
    23

到了这里，关于matlab基础知识加矩阵运算初步的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！