目录
一、什么是堆排序
1.1 堆的定义
1.2 堆排序的定义
1.3 堆排序的优势
二、堆排序的实现
2.1 堆排序的基本思路
2.2 堆排序的具体实现
2.3 堆排序的时间复杂度
三、C++实现堆排序
3.1 C++实现堆的基本操作
3.2 C++实现堆排序
四、堆排序的应用
4.1 堆排序在优先队列中的应用
4.2 堆排序在求Top K问题中的应用
五、总结
一、什么是堆排序
1.1 堆的定义
堆是一种特殊的树形数据结构,它满足以下两个条件:
1. 堆是一棵完全二叉树;
2. 堆中每个节点的值都大于等于(或小于等于)其子节点的值。
堆分为大根堆和小根堆,大根堆中每个节点的值都大于等于其子节点的值,小根堆中每个节点的值都小于等于其子节点的值。
1.2 堆排序的定义
堆排序是一种基于堆的排序算法,它的基本思想是将待排序的序列构建成一个堆,然后依次取出堆顶元素,直到堆为空。
1.3 堆排序的优势
堆排序的优势在于它的时间复杂度为O(nlogn),并且它是一种原地排序算法,不需要额外的存储空间。
二、堆排序的实现
2.1 堆排序的基本思路
堆排序的基本思路是将待排序的序列构建成一个堆,然后依次取出堆顶元素,直到堆为空。
具体实现过程如下:
1. 将待排序的序列构建成一个堆;
2. 取出堆顶元素,将堆的最后一个元素放到堆顶,然后重新调整堆,使其满足堆的性质;
3. 重复步骤2,直到堆为空。
2.2 堆排序的具体实现
堆排序的具体实现分为两个步骤:构建堆和调整堆。
构建堆的过程:
1. 从最后一个非叶子节点开始,依次向上调整堆,使其满足堆的性质;
2. 重复步骤1,直到根节点。
调整堆的过程:
1. 取出堆顶元素,将堆的最后一个元素放到堆顶;
2. 从堆顶开始向下调整堆,使其满足堆的性质。
2.3 堆排序的时间复杂度
堆排序的时间复杂度为O(nlogn),其中n为待排序序列的长度。
三、C++实现堆排序
3.1 C++实现堆的基本操作
C++中可以使用STL中的priority_queue来实现堆的基本操作,priority_queue是一个优先队列,它的底层实现是堆。
priority_queue的基本操作如下:
1. push(x):将x插入到堆中;
2. pop():删除堆顶元素;
3. top():返回堆顶元素;
4. size():返回堆的大小;
5. empty():判断堆是否为空。
3.2 C++实现堆排序
C++实现堆排序的代码如下:
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
void heap_sort(vector<int>& nums) {
priority_queue<int, vector<int>, greater<int>> q;
for (auto num : nums) {
q.push(num);
}
nums.clear();
while (!q.empty()) {
nums.push_back(q.top());
q.pop();
}
}
int main() {
vector<int> nums = {3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5};
heap_sort(nums);
for (auto num : nums) {
cout << num << " ";
}
cout << endl;
return 0;
}四、堆排序的应用
4.1 堆排序在优先队列中的应用
堆排序在优先队列中的应用非常广泛,优先队列是一种特殊的队列,它的元素按照一定的优先级进行排序,每次取出的元素都是优先级最高的元素。
优先队列可以使用堆来实现,堆中的元素按照优先级排序,每次取出堆顶元素即可。
4.2 堆排序在求Top K问题中的应用
堆排序在求Top K问题中也有广泛的应用,Top K问题是指从一个序列中找出前K个最大(或最小)的元素。
堆排序可以使用小根堆来解决Top K问题,将序列中的前K个元素构建成一个小根堆,然后依次遍历序列中的剩余元素,如果元素比堆顶元素大,则将堆顶元素替换为该元素,并重新调整堆,使其满足小根堆的性质。文章来源:https://www.toymoban.com/news/detail-495693.html
五、总结
堆排序是一种基于堆的排序算法,它的时间复杂度为O(nlogn),并且它是一种原地排序算法,不需要额外的存储空间。堆排序在优先队列和Top K问题中都有广泛的应用。C++中可以使用STL中的priority_queue来实现堆的基本操作。文章来源地址https://www.toymoban.com/news/detail-495693.html
到了这里,关于数据结构-堆排序的定义与思路实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!






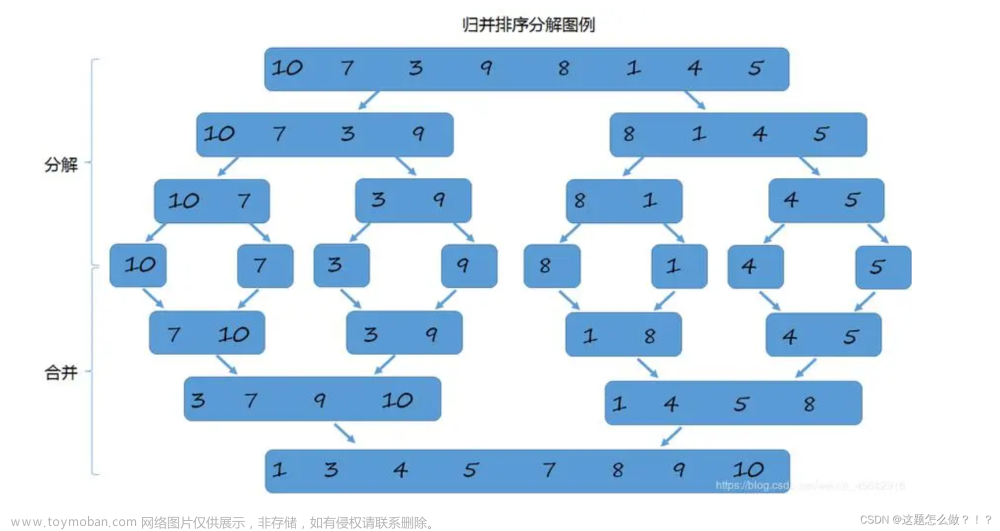
![[数据结构 -- 手撕排序算法第七篇] 递归实现归并排序](https://imgs.yssmx.com/Uploads/2024/02/573259-1.png)





