目录
一、前言:密码学有什么用?
二、单向散列函数
1、单向函数
2、散列函数
3、单向散列函数
三、怎么解决完整性问题
四、如何设置合适的安全强度
一、前言:密码学有什么用?


二、单向散列函数
单向散列函数就是用来解决“信息完整性”这一问题的。
下面先介绍一下单向函数和散列函数。
1、单向函数
概念:正向计算容易,逆向计算困难的函数。
2、散列函数
概念:把任意大小的输入,转成固定长度的数据的函数。
通常把转换后的数据称为散列值(哈希值)。
散列值碰撞:存在两个或多个数据的散列值相同。
如何降低散列值碰撞的可能?让散列值长度更长。
但同时也要权衡好性能问题(一个好的散列函数,散列值应该是均匀分布的)。
3、单向散列函数
既是单向函数,又是散列函数。
核心:
☆逆向运算困难
☆构造碰撞困难
雪崩效应
输入数据的微小变化,就会导致输出数据的巨大变化。
严格雪崩效应指的是,如果输入数据的一位反转,输出数据的每一位都有50%的概率会发生变化。
一个使用于密码学的单向散列函数,就应该具有雪崩效应的特点,如果一个单向散列函数具有雪崩效应,那么对于给定的数据,构造出一个新的、具有相同散列值的数据是困难的。
三、怎么解决完整性问题
完整性是什么?
数据未经授权,不可更改。
由于逆向运算困难,虽然存在具有相同散列值的两个或者多个数据,但是对于一个好的单向散列函数来说,刻意寻找这样的数据是困难的。如果困难程度足够大,我们就有足够信心认为,如果散列值没有变化,它对应的输入数据也没有变化。
所以,单向函数和散列函数的组合,单向散列函数,就可以帮助我们解决完整性问题。
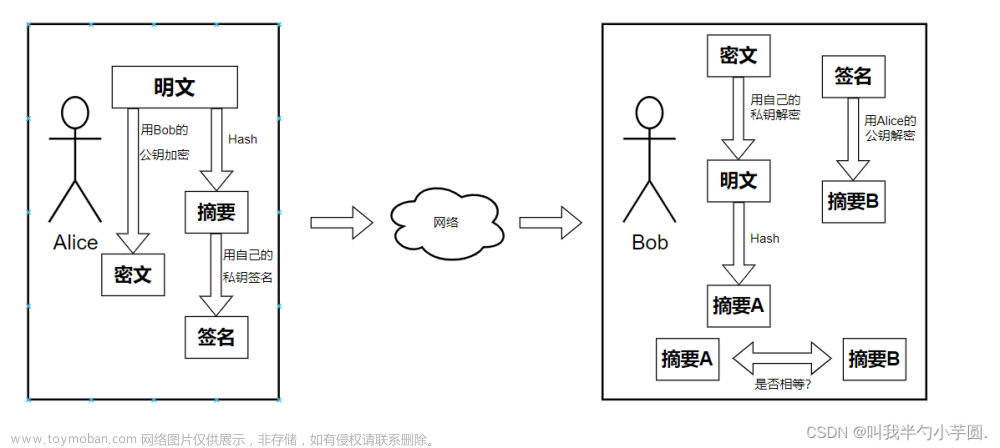
假如我们收到了一段数据,我们就可以重新计算这段数据的散列值。如果我们还可以获得数据发送者计算的散列值,我们就可以对比新计算的散列值和接收到的散列值。如果两个散列值是相同的,我们就可以认为这段数据是完整的;否则,这段数据就是被篡改过的。
该选择什么样的单向散列函数,它的破解难道才能足够大?稍后讲解
怎么能够安全地获得数据发送者计算的散列值? 晚些讲解
应用举例:
如在这个网站中,我们下载的文件可以生成一个MD5散列值,与它网站中给出的MD5值进行比对,如果是一样的,说明我们下载的文件没有篡改。


四、如何设置合适的安全强度
通常用“位”来表述。
N位的安全强度表示破解一个算法需要2^N(2的N次方)次运算。
18位,按现在的计算机运算速度计算,大约只需要4.34分钟。
64位,破解成本大概是5万美元左右。
128位,按现有的计算能力,破解它需要一千万个十亿年。
安全强度会变吗?
一个算法的安全强度表示一成不变的,随着安全分析的进步,几乎所有密码学算法的安全强度都会衰减。一个好的安全协议,一个考虑备份计划和应急计划。
使用多大的安全强度?
推荐指标:
美国的NIST
德国的BSI文章来源:https://www.toymoban.com/news/detail-495994.html
欧洲的ECRYPT-CSA文章来源地址https://www.toymoban.com/news/detail-495994.html
到了这里,关于单向散列函数(哈希)【密码学】(一)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!