文章目录
- 一、问题的描述
- 二、系统功能设计
- 三、各个代码部分
- 四、整体代码及其运行
- 五、总结
前言
建立与输出二叉树--C语言实现
一、问题描述
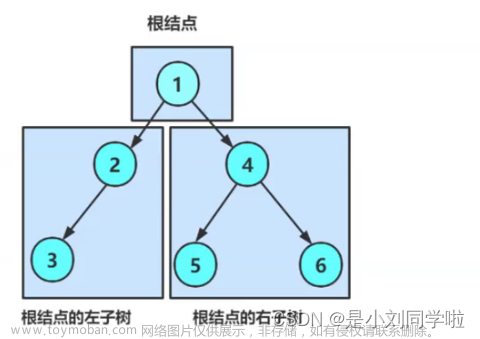
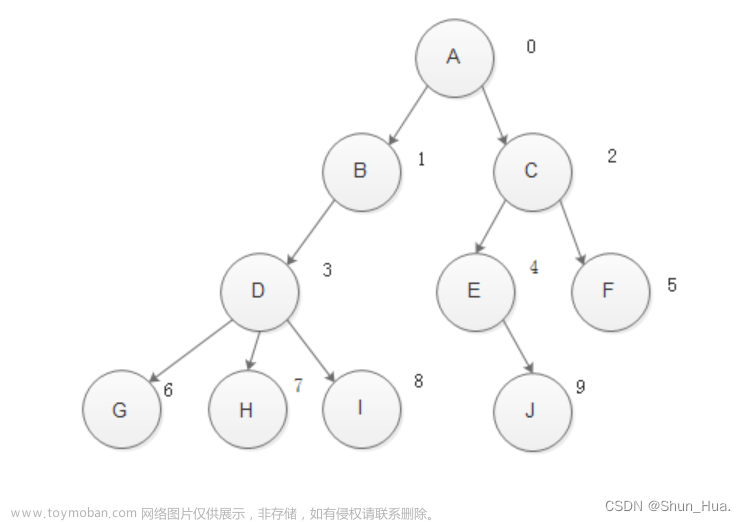
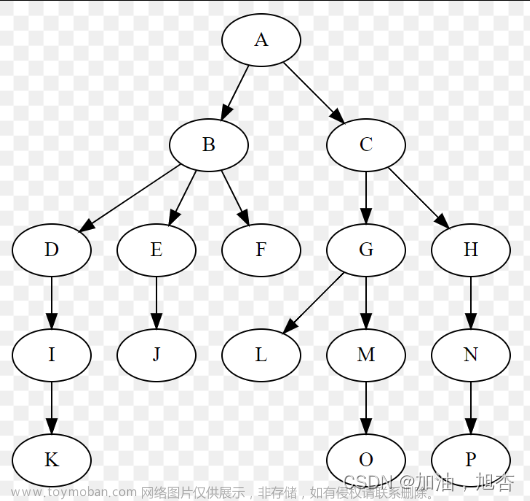
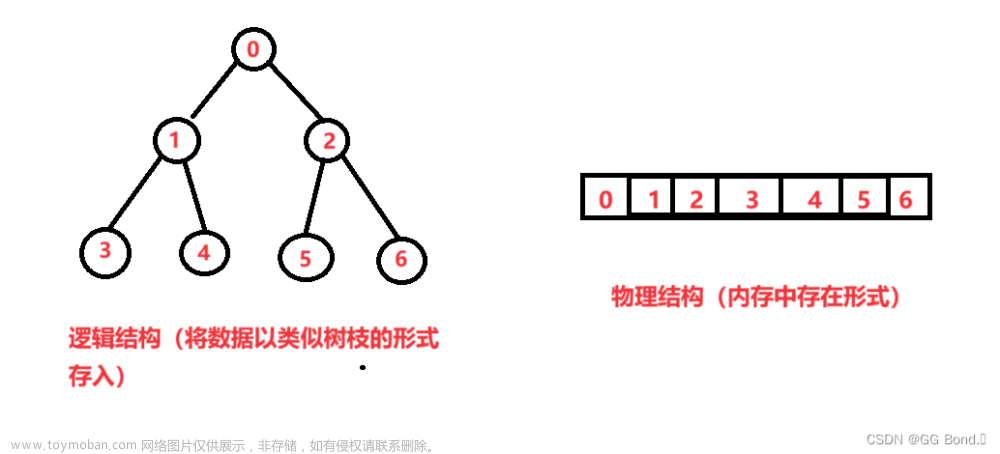
二叉树是一种特殊的树结构,也是最常见的树结构,二叉树的存储和处理比一般的树简单,而一般的树都能通过转换得到与子对应的二叉树。因此我们需要设计一个二叉树来了解树的各个功能。
文章来源地址https://www.toymoban.com/news/detail-496104.html
二、系统功能设计
1、需要设计的功能有:
- 1、以树状形式输出
- 2、以先序、中序、后序遍历输出
- 3、二叉树的节点总数
- 4、二叉树的叶子节点数
- 5、二叉树的深度
2、主界面如下:
 3、主界面代码如下:
3、主界面代码如下:
void menu()
{
printf("---------------------------欢迎来到二叉树的世界--------------------------------\n");
printf(" 1.以树状形式输出 \n");
printf(" 2.先序、中序、后续遍历\n");
printf(" 3.二叉树的节点总数 \n");
printf(" 4.二叉树的叶子总数 \n");
printf(" 5.二叉树的深度 \n");
printf(" 6.退出二叉树的世界 \n");
printf("-------------------------------------------------------------------------------\n");
}
三、各个代码部分
1、建立二叉树
1、主要以链表的方式存储
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define queuesize 100
typedef char Elemtype;
typedef struct node{
Elemtype date;//结点数据域
struct node *lchild, *rchild;//左右孩子指针
}BiTree;
//链式存储2、输入各个节点来创造树,以先序遍历输入,空格为空节点
BiTree *creat_tree()
{
Elemtype ch;
BiTree *root;
scanf("%c",&ch); // 输入要创建二叉树的根结点数据
if(ch==' ') // 判断二叉树是否为空的二叉树
root=NULL; // 如果是空的二叉树则二叉树的根结点指针为空
else // 如果不是则创建二叉树的根结点
{
root=(BiTree*)malloc(sizeof(BiTree));
root->date=ch; // 将输入的数据存储在根结点的数据域中
root->lchild=creat_tree();
root->rchild=creat_tree();
}
return root;
}
//创建二叉树2、以树状形式输出
//按树状打印二叉树
void PrintTree(BiTree *t,int h)
{
if(t==NULL) return;
PrintTree(t->rchild,h+1); /*先序打印右子树*/
int i;
for(i=0;i<h;i++) printf(" ");
printf("%c\n",t->date); /*输出结点*/
PrintTree(t->lchild,h+1); /*先序打印右子树*/
}效果如下:

3、先序、中序、后序遍历
//先序遍历递归实现
void Preorder(BiTree *t)
{
if(t!=NULL){
printf("%c ",t->date);//访问根结点
Preorder(t->lchild);//先序遍历左子树
Preorder(t->rchild);//先序遍历右子树
}
}
//中序遍历递归
void Inorder(BiTree *t)
{
if(t!=NULL){
Inorder(t->lchild);
printf("%c ",t->date);
Inorder(t->rchild);
}
}
//后序遍历递归
void postorder(BiTree *t)
{
if(t!=NULL){
postorder(t->lchild);
postorder(t->rchild);
printf("%c ",t->date);
}
}效果如下:

4、二叉树的节点总数
//统计二叉树节点总数
int countsum(BiTree *t)
{
int m,n;
if(t==NULL){
return 0;
}else{
m = countsum(t->lchild);
n = countsum(t->rchild);
return m+n+1;
}
}效果如下:

5、二叉树的叶子节点总数
//叶子节点总数
int countbitree(BiTree *t)
{
int m,n;
if(t==NULL){
return 0;
}
//左右子树都为空时
if(t->lchild==NULL&&t->rchild==NULL){
return 1;
}else{
m = countbitree(t->lchild);
n = countbitree(t->rchild);
return (m+n);
}
}效果如下:

6、树的深度
//树的高度
int depthbitree(BiTree *t)
{
int m,n;
//空树的高度为0
if(t==NULL){
return 0;
}else{
m = depthbitree(t->lchild);//求左子树的高度
n = depthbitree(t->rchild);//求右子树的高度
}
if(m>n){
return m+1;
}else{
return n+1;
}
}效果如下:

四、整体代码及其整体运行
1、所有代码如下:建议将子函数放在另一个文件里,与主函数区分开。
#include <stdio.h>
#include <stdlib.h>
typedef char Elemtype;
typedef struct node{
Elemtype date;//结点数据域
struct node *lchild, *rchild;//左右孩子指针
}BiTree;
//链式存储
void menu();//菜单
BiTree *creat_tree();//树的创建
void PrintTree(BiTree *t,int h) ;//树的树状形式输出
void Preorder(BiTree *t);//树的先序遍历
void Inorder(BiTree *t);//树的中序遍历
void postorder(BiTree *t);//树的后续遍历
int countsum(BiTree *t);//树的节点总数
int countbitree(BiTree *t);//树的叶子节点总数
int depthbitree(BiTree *t);//树的深度
void menu()
{
printf("---------------------------欢迎来到二叉树的世界--------------------------------\n");
printf(" 1.以树状形式输出 \n");
printf(" 2.先序、中序、后续遍历\n");
printf(" 3.二叉树的节点总数 \n");
printf(" 4.二叉树的叶子总数 \n");
printf(" 5.二叉树的深度 \n");
printf(" 6.退出二叉树的世界 \n");
printf("-------------------------------------------------------------------------------\n");
}
//创建二叉树
BiTree *creat_tree()
{
Elemtype ch;
BiTree *root;
scanf("%c",&ch); // 输入要创建二叉树的根结点数据
if(ch==' ') // 判断二叉树是否为空的二叉树
root=NULL; // 如果是空的二叉树则二叉树的根结点指针为空
else // 如果不是则创建二叉树的根结点
{
root=(BiTree*)malloc(sizeof(BiTree));
root->date=ch; // 将输入的数据存储在根结点的数据域中
root->lchild=creat_tree();
root->rchild=creat_tree();
}
return root;
}
//按树状打印二叉树
void PrintTree(BiTree *t,int h)
{
if(t==NULL) return;
PrintTree(t->rchild,h+1); /*先序打印右子树*/
int i;
for(i=0;i<h;i++) printf(" ");
printf("%c\n",t->date); /*输出结点*/
PrintTree(t->lchild,h+1); /*先序打印右子树*/
}
//先序遍历递归实现
void Preorder(BiTree *t)
{
if(t!=NULL){
printf("%c ",t->date);//访问根结点
Preorder(t->lchild);//先序遍历左子树
Preorder(t->rchild);//先序遍历右子树
}
}
//中序遍历递归
void Inorder(BiTree *t)
{
if(t!=NULL){
Inorder(t->lchild);
printf("%c ",t->date);
Inorder(t->rchild);
}
}
//后序遍历递归
void postorder(BiTree *t)
{
if(t!=NULL){
postorder(t->lchild);
postorder(t->rchild);
printf("%c ",t->date);
}
}
//统计二叉树节点总数
int countsum(BiTree *t)
{
int m,n;
if(t==NULL){
return 0;
}else{
m = countsum(t->lchild);
n = countsum(t->rchild);
return m+n+1;
}
}
//叶子节点总数
int countbitree(BiTree *t)
{
int m,n;
if(t==NULL){
return 0;
}
//左右子树都为空时
if(t->lchild==NULL&&t->rchild==NULL){
return 1;
}else{
m = countbitree(t->lchild);
n = countbitree(t->rchild);
return (m+n);
}
}
//树的高度
int depthbitree(BiTree *t)
{
int m,n;
//空树的高度为0
if(t==NULL){
return 0;
}else{
m = depthbitree(t->lchild);//求左子树的高度
n = depthbitree(t->rchild);//求右子树的高度
}
if(m>n){
return m+1;
}else{
return n+1;
}
}
int main()
{
BiTree *t;
menu();
int x;
printf("请输入根节点的数据:");
t = creat_tree();
printf("请选择你的项目:");
scanf("%d",&x);
while(x!=6){
switch(x){
case 1:
PrintTree(t,1);
break;
case 2:
printf("先序遍历:");
Preorder(t);
printf("\n");
printf("中序遍历:");
Inorder(t);
printf("\n");
printf("后序遍历: ");
postorder(t);
printf("\n");
break;
case 3:
printf("二叉树的节点总数为:");
int a = countsum(t);
printf("%d\n",a);
break;
case 4:
printf("树的叶子节点总数为:");
int b = countbitree(t);
printf("%d\n",b);
break;
case 5:
printf("树的高度为:");
int c = depthbitree(t);
printf("%d\n",c);
break;
case 6:
break;
default:
printf("输入项目有误!");
}
printf("请选择你的项目:");
scanf("%d",&x);
}
printf("已成功退出树世界!");
return 0;
}
2、整体运行结果如下:

五、总结
太多了不会?跟着我的代码敲,熟能生巧,一个一个模块去做,分治法大事化小。看着代码自己打一遍,能运行就是成功。文章来源:https://www.toymoban.com/news/detail-496104.html
到了这里,关于数据结构--建立与输出二叉树的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!