目录
6-1 线性表元素的区间删除 6-2 有序表的插入
6-3 合并两个有序数组 6-4 顺序表操作集
6-5 递增的整数序列链表的插入 6-6 删除单链表偶数节点
6-7 逆序数据建立链表 6-8 求链表的倒数第m个元素
6-9 两个有序链表序列的合并 6-10二叉树的遍历
6-11 二叉树的非递归遍历 6-12 求二叉树高度
6-13 邻接矩阵存储图的深度优先遍历 6-14 邻接表存储图的广度优先遍历
7-1 一元多项式的乘法与加法运算 7-2 符号配对
7-3 银行业务队列简单模拟 7-4 顺序存储的二叉树的最近的公共祖先问题
7-5 修理牧场 7-6 公路村村通
7-7 畅通工程之最低成本建设问题 7-8 最短工期
7-9 哈利·波特的考试 7-10 旅游规划
7-11 QQ帐户的申请与登陆 7-12 人以群分
7-13 寻找大富翁 7-14 PAT排名汇总
精简版:郑州轻工业大学2022-2023(2)数据结构题目集(精简版)
6-1 线性表元素的区间删
给定一个顺序存储的线性表,请设计一个函数删除所有值大于min而且小于max的元素。删除后表中剩余元素保持顺序存储,并且相对位置不能改变。
函数接口定义:
List Delete( List L, ElementType minD, ElementType maxD );
其中List结构定义如下:
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素在数组中的位置 */
};
L是用户传入的一个线性表,其中ElementType元素可以通过>、==、<进行比较;minD和maxD分别为待删除元素的值域的下、上界。函数Delete应将Data[]中所有值大于minD而且小于maxD的元素删除,同时保证表中剩余元素保持顺序存储,并且相对位置不变,最后返回删除后的表。
裁判测试程序样例:
#include <stdio.h>
#define MAXSIZE 20
typedef int ElementType;
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
List ReadInput(); /* 裁判实现,细节不表。元素从下标0开始存储 */
void PrintList( List L ); /* 裁判实现,细节不表 */
List Delete( List L, ElementType minD, ElementType maxD );
int main()
{
List L;
ElementType minD, maxD;
int i;
L = ReadInput();
scanf("%d %d", &minD, &maxD);
L = Delete( L, minD, maxD );
PrintList( L );
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
10
4 -8 2 12 1 5 9 3 3 10
0 4
输出样例:
4 -8 12 5 9 10
代码长度限制 16 KB
时间限制 200 ms
内存限制 64 MB
参考代码:
List Delete(List L, ElementType minD, ElementType maxD) {
int i, p = 0;
for (i = 0; i <= L->Last; i++) {
if (L->Data[i] <= minD || L->Data[i] >= maxD) {
L->Data[p++] = L->Data[i];
}
}
L->Last = p - 1;
return L;
}
6-2 有序表的插入
设顺序表中的数据元素是按值非递减有序排列的,试编写一算法,将x插入到顺序表的适当位置上,以保持顺序表的有序性。
函数接口定义:
void ListInsertSort(SqList *L, DataType x);
其中 L 和 x 都是用户传入的参数。 L 表示顺序表, x 是要插入的元素。
裁判测试程序样例:
#include"stdio.h"
#define LISTSIZE 100
typedef int DataType;
typedef struct{
DataType items[LISTSIZE];
int length;
}SqList;
/* 本题要求函数 */
void ListInsertSort(SqList *L, DataType x);
int InitList(SqList *L)
{/*L为指向顺序表的指针*/
L->length=0;
return 1;
}
int ListLength(SqList L)
{/*L为顺序表*/
return L.length;
}
int ListInsert(SqList *L,int pos,DataType item)
{/*L为指向顺序表的指针,pos为插入位置,item为待插入的数据元素*/
int i;
if(L->length>=LISTSIZE){
printf("顺序表已满,无法进行插入操作!");return 0;}
if(pos<=0 || pos>L->length+1){
printf("插入位置不合法,其取值范围应该是[1,length+1]");
return 0; }
for(i=L->length-1; i>=pos-1; i--) /*移动数据元素*/
L->items[i+1]=L->items[i];
L->items[pos-1]=item; /*插入*/
L->length++; /*表长增一*/
return 1; }
int TraverseList(SqList L)
{/*L为顺序表*/
int i;
for(i=0;i<L.length;i++) printf("%d ",L.items[i]);
printf("\n");
return 1;
}
void main()
{
int i,input,x;
SqList L1; //定义顺序表
InitList(&L1); //初始化建空表
for(i=0;;i++)
{
scanf("%d",&input);
if(input==-1)break;
ListInsert(&L1, i+1, input); //插入数据
}
scanf("%d",&x);
ListInsertSort(&L1, x); // 本题要求函数在主函数中的调用
TraverseList(L1); //遍历
}
/* 请在这里填写答案 */
输入样例:
在这里给出一组输入。例如:
1 3 6 7 8 9 -1
3
输出样例:
在这里给出相应的输出。例如:
1 3 3 6 7 8 9 代码长度限制 16 KB
时间限制 200 ms
内存限制 64 MB
参考代码:
void ListInsertSort(SqList *L, DataType x) {
int i;
int temp = 1;
for (i = 0; L->items[i] < x; i++) {
temp++;
}
ListInsert(L,temp,x);
}6-3 合并两个有序数组
要求实现一个函数merge,将长度为m的升序数组a和长度为n的升序数组b合并到一个新的数组c,合并后的数组仍然按升序排列。
函数接口定义:
void printArray(int* arr, int arr_size); /* 打印数组,细节不表 */
void merge(int* a, int m, int* b, int n, int* c); /* 合并a和b为c */
其中a和b是按升序排列的数组,m和n分别为数组a、b的长度;c为合并后的升序数组。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
void printArray(int* arr, int arr_size); /* 打印数组,细节不表 */
void merge(int* a, int m, int* b, int n, int* c); /* 合并a和b为c */
int main(int argc, char const *argv[])
{
int m, n, i;
int *a, *b, *c;
scanf("%d", &m);
a = (int*)malloc(m * sizeof(int));
for (i = 0; i < m; i++) {
scanf("%d", &a[i]);
}
scanf("%d", &n);
b = (int*)malloc(n * sizeof(int));
for (i = 0; i < n; i++) {
scanf("%d", &b[i]);
}
c = (int*)malloc((m + n) * sizeof(int));
merge(a, m, b, n, c);
printArray(c, m + n);
return 0;
}
/* 请在这里填写答案 */
输入样例:
输入包含两行。
第一行为有序数组a,其中第一个数为数组a的长度m,紧接着m个整数。
第二行为有序数组b,其中第一个数为数组b的长度n,紧接着n个整数。
7 1 2 14 25 33 73 84
11 5 6 17 27 68 68 74 79 80 85 87
输出样例:
输出为合并后按升序排列的数组。
1 2 5 6 14 17 25 27 33 68 68 73 74 79 80 84 85 87代码长度限制 16 KB
时间限制 200 ms
内存限制 64 MB
参考答案:
void merge(int *a, int m, int *b, int n, int *c) {
int i, j, k;
while (i < m && j < n) {
if (a[i] < b[j])
c[k++] = a[i++];
else
c[k++] = b[j++];
}
while (i < m) {
c[k++] = a[i++];
}
while (j < n) {
c[k++] = b[j++];
}
}6-4 顺序表操作集
本题要求实现顺序表的操作集。
函数接口定义:
List MakeEmpty();
Position Find( List L, ElementType X );
bool Insert( List L, ElementType X, Position P );
bool Delete( List L, Position P );
其中List结构定义如下:
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
各个操作函数的定义为:
List MakeEmpty():创建并返回一个空的线性表;
Position Find( List L, ElementType X ):返回线性表中X的位置。若找不到则返回ERROR;
bool Insert( List L, ElementType X, Position P ):将X插入在位置P并返回true。若空间已满,则打印“FULL”并返回false;如果参数P指向非法位置,则打印“ILLEGAL POSITION”并返回false;
bool Delete( List L, Position P ):将位置P的元素删除并返回true。若参数P指向非法位置,则打印“POSITION P EMPTY”(其中P是参数值)并返回false。裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 5
#define ERROR -1
typedef enum {false, true} bool;
typedef int ElementType;
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
List MakeEmpty();
Position Find( List L, ElementType X );
bool Insert( List L, ElementType X, Position P );
bool Delete( List L, Position P );
int main()
{
List L;
ElementType X;
Position P;
int N;
L = MakeEmpty();
scanf("%d", &N);
while ( N-- ) {
scanf("%d", &X);
if ( Insert(L, X, 0)==false )
printf(" Insertion Error: %d is not in.\n", X);
}
scanf("%d", &N);
while ( N-- ) {
scanf("%d", &X);
P = Find(L, X);
if ( P == ERROR )
printf("Finding Error: %d is not in.\n", X);
else
printf("%d is at position %d.\n", X, P);
}
scanf("%d", &N);
while ( N-- ) {
scanf("%d", &P);
if ( Delete(L, P)==false )
printf(" Deletion Error.\n");
if ( Insert(L, 0, P)==false )
printf(" Insertion Error: 0 is not in.\n");
}
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
6
1 2 3 4 5 6
3
6 5 1
2
-1 6
输出样例:
FULL Insertion Error: 6 is not in.
Finding Error: 6 is not in.
5 is at position 0.
1 is at position 4.
POSITION -1 EMPTY Deletion Error.
FULL Insertion Error: 0 is not in.
POSITION 6 EMPTY Deletion Error.
FULL Insertion Error: 0 is not in.代码长度限制 16 KB
时间限制 200 ms
内存限制 64 MB
参考代码:
List MakeEmpty() {
List list;
list = (List) malloc(sizeof(struct LNode));
list->Last = -1;
return list;
}
Position Find(List L, ElementType X) {
int i;
for (i = 0; i < MAXSIZE; i++) {
if (L->Data[i] == X)
return i;
}
return ERROR;
}
bool Insert(List L, ElementType X, Position P) {
int i;
if (L->Last == MAXSIZE - 1) {
printf("FULL");
return false;
}
if (P < 0 || P > L->Last + 1) {
printf("ILLEGAL POSITION");
return false;
}
for (i = L->Last; i >= P; i--) {
L->Data[i + 1] = L->Data[i];
}
L->Data[P] = X;
L->Last++;
return true;
}
bool Delete(List L, Position P) {
int i;
if (P < 0 || P > L->Last) {
printf("POSITION %d EMPTY", P);
return false;
}
for (i = P; i < L->Last; i++) {
L->Data[i] = L->Data[i + 1];
}
L->Last--;
return true;
}6-5 递增的整数序列链表的插入
本题要求实现一个函数,在递增的整数序列链表(带头结点)中插入一个新整数,并保持该序列的有序性。
函数接口定义:
List Insert( List L, ElementType X );
其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */
L是给定的带头结点的单链表,其结点存储的数据是递增有序的;函数Insert要将X插入L,并保持该序列的有序性,返回插入后的链表头指针。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node {
ElementType Data;
PtrToNode Next;
};
typedef PtrToNode List;
List Read(); /* 细节在此不表 */
void Print( List L ); /* 细节在此不表 */
List Insert( List L, ElementType X );
int main()
{
List L;
ElementType X;
L = Read();
scanf("%d", &X);
L = Insert(L, X);
Print(L);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
5
1 2 4 5 6
3
输出样例:
1 2 3 4 5 6 代码长度限制 16 KB
时间限制 200 ms
内存限制 64 MB
参考代码:
List Insert(List L, ElementType X) {
List p, s;
p = L;
s = (List) malloc(sizeof(struct Node));
s->Data = X;
while (p->Next && p->Next->Data < X) {
p = p->Next;
}
s->Next = p->Next;
p->Next = s;
return L;
}6-6 删除单链表偶数节点
本题要求实现两个函数,分别将读入的数据存储为单链表、将链表中偶数值的结点删除。链表结点定义如下:
struct ListNode {
int data;
struct ListNode *next;
};
函数接口定义:
struct ListNode *createlist();
struct ListNode *deleteeven( struct ListNode *head );
函数createlist从标准输入读入一系列正整数,按照读入顺序建立单链表。当读到−1时表示输入结束,函数应返回指向单链表头结点的指针。
函数deleteeven将单链表head中偶数值的结点删除,返回结果链表的头指针。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
struct ListNode {
int data;
struct ListNode *next;
};
struct ListNode *createlist();
struct ListNode *deleteeven( struct ListNode *head );
void printlist( struct ListNode *head )
{
struct ListNode *p = head;
while (p) {
printf("%d ", p->data);
p = p->next;
}
printf("\n");
}
int main()
{
struct ListNode *head;
head = createlist();
head = deleteeven(head);
printlist(head);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
1 2 2 3 4 5 6 7 -1
输出样例:
1 3 5 7 代码长度限制 16 KB
时间限制 200 ms
内存限制 64 MB
参考代码:
struct ListNode *createlist() {
int m;
struct ListNode *p, *s, *l;
p = (struct ListNode *) malloc(sizeof(struct ListNode));
scanf("%d", &m);
if (m == -1)
return NULL;
p->data = m;
p->next = NULL;
s = p;
while (1) {
scanf("%d", &m);
if (m == -1)
break;
l = (struct ListNode *) malloc(sizeof(struct ListNode));
l->data = m;
l->next = NULL;
s->next = l;
s = l;
}
return p;
}
struct ListNode *deleteeven(struct ListNode *head) {
struct ListNode *p = NULL, *s = NULL;
while (head && head->data % 2 == 0) {
p = head;
head = head->next;
free(p);
}
if (head == NULL)
return NULL;
s = head;
while (s->next) {
if (s->next->data % 2 == 0)
s->next = s->next->next;
else
s = s->next;
}
return head;
}6-7 逆序数据建立链表
本题要求实现一个函数,按输入数据的逆序建立一个链表。
函数接口定义:
struct ListNode *createlist();函数createlist利用scanf从输入中获取一系列正整数,当读到−1时表示输入结束。按输入数据的逆序建立一个链表,并返回链表头指针。链表节点结构定义如下:
struct ListNode {
int data;
struct ListNode *next;
};
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
struct ListNode {
int data;
struct ListNode *next;
};
struct ListNode *createlist();
int main()
{
struct ListNode *p, *head = NULL;
head = createlist();
for ( p = head; p != NULL; p = p->next )
printf("%d ", p->data);
printf("\n");
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
1 2 3 4 5 6 7 -1
输出样例:
7 6 5 4 3 2 1 代码长度限制 16 KB
时间限制 200 ms
内存限制 64 MB
参考代码:
struct ListNode *createlist() {
int m;
struct ListNode *head, *p;
head = (struct ListNode *) malloc(sizeof(struct ListNode));
head->next = NULL;
while (1) {
scanf("%d", &m);
if (m == -1)
break;
p = (struct ListNode *) malloc(sizeof(struct ListNode));
p->next = head->next;
p->data = m;
head->next = p;
}
return head->next;
}6-8 求链表的倒数第m个元素
请设计时间和空间上都尽可能高效的算法,在不改变链表的前提下,求链式存储的线性表的倒数第m(>0)个元素。
函数接口定义:
ElementType Find( List L, int m );
其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */
L是给定的带头结点的单链表;函数Find要将L的倒数第m个元素返回,并不改变原链表。如果这样的元素不存在,则返回一个错误标志ERROR。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
#define ERROR -1
typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node {
ElementType Data;
PtrToNode Next;
};
typedef PtrToNode List;
List Read(); /* 细节在此不表 */
void Print( List L ); /* 细节在此不表 */
ElementType Find( List L, int m );
int main()
{
List L;
int m;
L = Read();
scanf("%d", &m);
printf("%d\n", Find(L,m));
Print(L);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
5
1 2 4 5 6
3
输出样例:
4
1 2 4 5 6 代码长度限制 16 KB
时间限制 200 ms
内存限制 64 MB
参考代码:
ElementType Find(List L, int m) {
int i;
PtrToNode p, s;
p = s = L;
for (i = 0; i < m; i++) {
p = p->Next;
if (!p)
return ERROR;
}
while (p) {
s = s->Next;
p = p->Next;
}
return s->Data;
}6-9 两个有序链表序列的合并
本题要求实现一个函数,将两个链表表示的递增整数序列合并为一个非递减的整数序列。
函数接口定义:
List Merge( List L1, List L2 );其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */
L1和L2是给定的带头结点的单链表,其结点存储的数据是递增有序的;函数Merge要将L1和L2合并为一个非递减的整数序列。应直接使用原序列中的结点,返回归并后的带头结点的链表头指针。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node {
ElementType Data;
PtrToNode Next;
};
typedef PtrToNode List;
List Read(); /* 细节在此不表 */
void Print( List L ); /* 细节在此不表;空链表将输出NULL */
List Merge( List L1, List L2 );
int main()
{
List L1, L2, L;
L1 = Read();
L2 = Read();
L = Merge(L1, L2);
Print(L);
Print(L1);
Print(L2);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
3
1 3 5
5
2 4 6 8 10
输出样例:
1 2 3 4 5 6 8 10
NULL
NULL代码长度限制 16 KB
时间限制 200 ms
内存限制 64 MB
参考代码:
List Merge( List L1, List L2 )
{
List pa,pb,pc;
pa=L1->Next;
pb=L2->Next;
List L=(List)malloc(sizeof(List));
pc=L;
while(pa&&pb)
{
if(pa->Data>pb->Data)
{
pc->Next=pb;
pb=pb->Next;
}
else{
pc->Next=pa;
pa=pa->Next;
}
pc=pc->Next;
}
if(pa)
pc->Next = pa;
if(pb)
pc->Next = pb;
L1->Next=NULL;
L2->Next=NULL;
return L;
}6-10 二叉树的遍历
本题要求给定二叉树的4种遍历。
函数接口定义:
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
void LevelorderTraversal( BinTree BT );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
要求4个函数分别按照访问顺序打印出结点的内容,格式为一个空格跟着一个字符。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
BinTree CreatBinTree(); /* 实现细节忽略 */
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
void LevelorderTraversal( BinTree BT );
int main()
{
BinTree BT = CreatBinTree();
printf("Inorder:"); InorderTraversal(BT); printf("\n");
printf("Preorder:"); PreorderTraversal(BT); printf("\n");
printf("Postorder:"); PostorderTraversal(BT); printf("\n");
printf("Levelorder:"); LevelorderTraversal(BT); printf("\n");
return 0;
}
/* 你的代码将被嵌在这里 */
输出样例(对于图中给出的树):
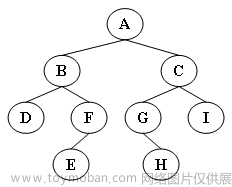
Inorder: D B E F A G H C I
Preorder: A B D F E C G H I
Postorder: D E F B H G I C A
Levelorder: A B C D F G I E H代码长度限制 16 KB
时间限制 400 ms
内存限制 64 MB
参考代码:
void InorderTraversal(BinTree BT) {//中序遍历
if (BT) {
InorderTraversal(BT->Left);
printf(" %c", BT->Data);
InorderTraversal(BT->Right);
}
}
void PreorderTraversal(BinTree BT) {//先序遍历
if (BT) {
printf(" %c", BT->Data);
PreorderTraversal(BT->Left);
PreorderTraversal(BT->Right);
}
}
void PostorderTraversal(BinTree BT) {//后序遍历
if (BT) {
PostorderTraversal(BT->Left);
PostorderTraversal(BT->Right);
printf(" %c", BT->Data);
}
}
void LevelorderTraversal(BinTree BT) {
BinTree B[100];//结构体数组
BinTree T;
int i = 0, j = 0;
if (!BT)return;//树为空,返回
if (BT)//不为空
{
B[i++] = BT;//根节点入队
while (i != j)//队列不空
{
T = B[j++];//出队
printf(" %c", T->Data);
if (T->Left) B[i++] = T->Left;
if (T->Right) B[i++] = T->Right;
}
}
} 6-11 二叉树的非递归遍历
本题要求用非递归的方法实现对给定二叉树的 3 种遍历。
函数接口定义:
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
int flag;
};
要求 3 个函数分别按照访问顺序打印出结点的内容,格式为一个空格跟着一个字符。
此外,裁判程序中给出了堆栈的全套操作,可以直接调用。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef enum { false, true } bool;
typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
int flag;
};
/*------堆栈的定义-------*/
typedef Position SElementType;
typedef struct SNode *PtrToSNode;
struct SNode {
SElementType Data;
PtrToSNode Next;
};
typedef PtrToSNode Stack;
/* 裁判实现,细节不表 */
Stack CreateStack();
bool IsEmpty( Stack S );
bool Push( Stack S, SElementType X );
SElementType Pop( Stack S ); /* 删除并仅返回S的栈顶元素 */
SElementType Peek( Stack S );/* 仅返回S的栈顶元素 */
/*----堆栈的定义结束-----*/
BinTree CreateBinTree(); /* 裁判实现,细节不表 */
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
int main()
{
BinTree BT = CreateBinTree();
printf("Inorder:"); InorderTraversal(BT); printf("\n");
printf("Preorder:"); PreorderTraversal(BT); printf("\n");
printf("Postorder:"); PostorderTraversal(BT); printf("\n");
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
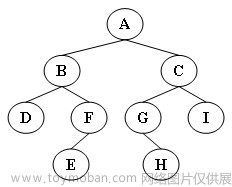
输出样例:
Inorder: D B E F A G H C I
Preorder: A B D F E C G H I
Postorder: D E F B H G I C A代码长度限制 16 KB
时间限制 400 ms
内存限制 64 MB
参考代码:
void InorderTraversal( BinTree BT ){//中序遍历
BinTree T=BT;
Stack S =CreateStack();
while(T||!IsEmpty(S)){
while(T!=NULL){
Push(S,T);
T=T->Left;
}
T=Pop(S);
printf(" %c",T->Data);
T=T->Right;
}
}
void PreorderTraversal( BinTree BT ){//先序遍历
BinTree T=BT;
Stack S =CreateStack();
while(T||!IsEmpty(S)){
while(T!=NULL){
Push(S,T);
printf(" %c",T->Data);
T=T->Left;
}
T=Pop(S);
T=T->Right;
}
}
void PostorderTraversal( BinTree BT ){//后序遍历
BinTree T=BT;
Stack S =CreateStack();
while(T||!IsEmpty(S)){
while(T!=NULL){
T->flag=0;
Push(S,T);
T=T->Left;
}
T=Peek(S);
if(T->flag==0){
T->flag++;
T=T->Right;
}
else{
T=Pop(S);
printf(" %c",T->Data);
T=NULL;
}
}
}6-12 求二叉树高度
本题要求给定二叉树的高度。
函数接口定义:
int GetHeight( BinTree BT );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
要求函数返回给定二叉树BT的高度值。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
BinTree CreatBinTree(); /* 实现细节忽略 */
int GetHeight( BinTree BT );
int main()
{
BinTree BT = CreatBinTree();
printf("%d\n", GetHeight(BT));
return 0;
}
/* 你的代码将被嵌在这里 */
输出样例(对于图中给出的树):
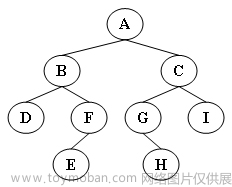
4代码长度限制 16 KB
时间限制 400 ms
内存限制 64 MB
参考代码:
int GetHeight(BinTree BT) {
int lNum, rNum, Height;
if (BT) {
lNum = GetHeight(BT->Left);
rNum = GetHeight(BT->Right);
if (lNum > rNum)
Height = lNum;
else
Height = rNum;
return Height + 1;
} else {
return 0;
}
}6-13 邻接矩阵存储图的深度优先遍历
试实现邻接矩阵存储图的深度优先遍历。
函数接口定义:
void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) );其中 MGraph 是邻接矩阵存储的图,定义如下
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
函数DFS应从第V个顶点出发递归地深度优先遍历图Graph,遍历时用裁判定义的函数Visit访问每个顶点。当访问邻接点时,要求按序号递增的顺序。题目保证V是图中的合法顶点。
裁判测试程序样例:
#include <stdio.h>
typedef enum {false, true} bool;
#define MaxVertexNum 10 /* 最大顶点数设为10 */
#define INFINITY 65535 /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
bool Visited[MaxVertexNum]; /* 顶点的访问标记 */
MGraph CreateGraph(); /* 创建图并且将Visited初始化为false;裁判实现,细节不表 */
void Visit( Vertex V )
{
printf(" %d", V);
}
void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) );
int main()
{
MGraph G;
Vertex V;
G = CreateGraph();
scanf("%d", &V);
printf("DFS from %d:", V);
DFS(G, V, Visit);
return 0;
}
/* 你的代码将被嵌在这里 */输入样例:给定图如下
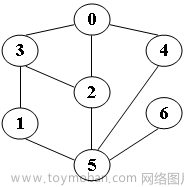
5
输出样例:
DFS from 5: 5 1 3 0 2 4 6
代码长度限制 16 KB
时间限制 400 ms
内存限制 64 MB
参考代码:
void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) ) {
Visit(V);
Visited[V]=true;
for(int i=0; i<Graph->Nv; i++) {
if(Graph->G[V][i]==1&&!Visited[i]) {
DFS(Graph,i,Visit);//进行递归
}
}
}
6-14 邻接表存储图的广度优先遍历
试实现邻接表存储图的广度优先遍历。
函数接口定义:
void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) );其中LGraph是邻接表存储的图,定义如下:
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV; /* 邻接点下标 */
PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};
/* 顶点表头结点的定义 */
typedef struct Vnode{
PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
AdjList G; /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
函数BFS应从第S个顶点出发对邻接表存储的图Graph进行广度优先搜索,遍历时用裁判定义的函数Visit访问每个顶点。当访问邻接点时,要求按邻接表顺序访问。题目保证S是图中的合法顶点。
裁判测试程序样例:
#include <stdio.h>
typedef enum {false, true} bool;
#define MaxVertexNum 10 /* 最大顶点数设为10 */
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV; /* 邻接点下标 */
PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};
/* 顶点表头结点的定义 */
typedef struct Vnode{
PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
AdjList G; /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
bool Visited[MaxVertexNum]; /* 顶点的访问标记 */
LGraph CreateGraph(); /* 创建图并且将Visited初始化为false;裁判实现,细节不表 */
void Visit( Vertex V )
{
printf(" %d", V);
}
void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) );
int main()
{
LGraph G;
Vertex S;
G = CreateGraph();
scanf("%d", &S);
printf("BFS from %d:", S);
BFS(G, S, Visit);
return 0;
}
/* 你的代码将被嵌在这里 */输入样例:给定图如下
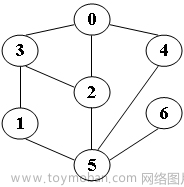
2
输出样例:
BFS from 2: 2 0 3 5 4 1 6
代码长度限制 16 KB
时间限制 400 ms
内存限制 64 MB
参考代码:
void BFS(LGraph Graph, Vertex S, void (*Visit)(Vertex)) {
Visited[S] = true;//标记起始点
Visit(S);
int queue[1000], front = 0, rear = 0;
queue[rear++] = S;//起始点入队列
PtrToAdjVNode temp;//temp就代表当前点的邻接点的下标
while (front < rear) {//队伍不为空
temp = Graph->G[queue[front++]].FirstEdge;
while (temp) {
int p = temp->AdjV;//把temp中的下标提取出来
if (!Visited[p]) {//如果p点没有被标记的话
Visited[p] = true;
Visit(p);
queue[rear++] = p;//储存在队列中
}
temp = temp->Next;//指向下一个邻接点
}
}
}7-1 一元多项式的乘法与加法运算
设计函数分别求两个一元多项式的乘积与和。
输入格式:
输入分2行,每行分别先给出多项式非零项的个数,再以指数递降方式输入一个多项式非零项系数和指数(绝对值均为不超过1000的整数)。数字间以空格分隔。
输出格式:
输出分2行,分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。数字间以空格分隔,但结尾不能有多余空格。零多项式应输出0 0。
输入样例:
4 3 4 -5 2 6 1 -2 0
3 5 20 -7 4 3 1
输出样例:
15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0
代码长度限制 16 KB
时间限制 200 ms
内存限制 64 MB
参考代码:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct LNode *List;
struct LNode {
ElementType coe;//系数
ElementType exp;//指数
List Next;//下一个节点
};
void Insert(List L, ElementType coe, ElementType exp);//插入
List Multi(List p1, List p2);//乘法
List Plus(List p1, List p2);//加法
int compare(List p1, List p2);//比较系数大小
int main() {
List p1, p2;
List p;
int num1, num2, coe, exp;
int i;
p1 = (List) malloc(sizeof(struct LNode));
p2 = (List) malloc(sizeof(struct LNode));
p1->Next = NULL;
p2->Next = NULL;
scanf("%d", &num1);
for (i = 0; i < num1; i++) {
scanf("%d %d", &coe, &exp);
Insert(p1, coe, exp);
}
scanf("%d", &num2);
for (i = 0; i < num2; i++) {
scanf("%d %d", &coe, &exp);
Insert(p2, coe, exp);
}
//乘法运算
p = Multi(p1->Next, p2->Next);
while (p) {
if (p->Next != NULL) {
printf("%d %d ", p->coe, p->exp);//非最后一个节点,不换行打印,后接空格
} else {
printf("%d %d\n", p->coe, p->exp);//最后一个节点,换行打印
}
p = p->Next;
}
//加法运算
p = Plus(p1->Next, p2->Next);
if (p) {
while (p) {
if (p->Next != NULL) {
printf("%d %d ", p->coe, p->exp);
} else {
printf("%d %d\n", p->coe, p->exp);
}
p = p->Next;
}
} else {//防止出现p1,p2抵消为零的情况
printf("0 0\n");
}
return 0;
}
/**
* 向链表中添加元素
* @param L 需要添加的链表
* @param coefficient 系数
* @param exponent 指数
*/
void Insert(List L, ElementType coe, ElementType exp) {
List s, p;
p = L;
while (p->Next)//找到最后一个节点
p = p->Next;
s = (List) malloc(sizeof(struct LNode));
s->Next = NULL;
s->coe = coe;
s->exp = exp;
p->Next = s;
}
/**
* 两个多项式相乘
* @param p1 代表多项式1的链表
* @param p2 代表多项式2的链表
* @return p 相乘后生成的新链表
*/
List Multi(List p1, List p2) {
List p, p1a, p2a, s;
int flag = 1;
p = (List) malloc(sizeof(struct LNode));
p->Next = NULL;
p1a = p1;
while (p1a) {
p2a = p2;//确保p1多项式中的每一项可以与p2多项式中的每一项分别相乘
s = (List) malloc(sizeof(struct LNode));
s->Next = NULL;
while (p2a) {//与p2多项式中的每一项分别相乘
Insert(s, p1a->coe * p2a->coe, p1a->exp + p2a->exp);
p2a = p2a->Next;
}
s = s->Next;
if (flag == 1) {
p = p->Next;
/*
* 如果是p1第一项与p2每一项相乘,那么先将链表p向后移一位,将头结点屏蔽
* 因为默认初始化的P1头结点有默认的exp = 0,coe = 0,这两个数据是多余的
* 如果不后移,那么头结点默认的数值0将会一直尾随整个乘法运算,导致最后的结果后面多两个0 0
*/
flag = 0;
}
p = Plus(p, s);//相加,确保同类项合并
p1a = p1a->Next;
free(s);
}
return p;
}
/**
* 比较两多项式指数大小
* @param p1 代表多项式1的链表
* @param p2 代表多项式2的链表
* @return 返回值为0时表示两指数相同,可以进行加法运算
*/
int compare(List p1, List p2) {
if (p1->exp > p2->exp)
return 1;//p1指数大
else if (p1->exp < p2->exp)
return -1;//p1指数小
else
return 0;//指数相同
}
/**
* 两个多项式相加
* @param p1 代表多项式1的链表
* @param p2 代表多项式2的链表
* @return p 相加后生成的新链表
*/
List Plus(List p1, List p2) {
List p, p1a, p2a;
int temp;
p = (List) malloc(sizeof(struct LNode));
p->Next = NULL;
p1a = p1;
p2a = p2;
while (p1a && p2a) {
temp = compare(p1a, p2a);
//判断指数大小,同指数才可以运算
switch (temp) {
case 1:
//当前p1a的指数大,将当前p1a的数据放入新链表
Insert(p, p1a->coe, p1a->exp);
p1a = p1a->Next;//p1a向后移动,p2a不改变
break;
case -1:
//当前p2a的指数大,将当前p2a的数据放入新链表
Insert(p, p2a->coe, p2a->exp);
p2a = p2a->Next;//p2a向后移动,p1a不改变
break;
case 0:
//指数相同,进行运算
if ((p1a->coe + p2a->coe) == 0) {
//系数为0,数据不放入新链表,直接将p1a和p2a后移
p1a = p1a->Next;
p2a = p2a->Next;
} else {
//数据放入新链表,p1a和p2a后移
Insert(p, p1a->coe + p2a->coe, p2a->exp);
p1a = p1a->Next;
p2a = p2a->Next;
}
break;
default:
break;
}
}
while (p1a) {
//p1a的项数多,将剩余项放入链表
Insert(p, p1a->coe, p1a->exp);
p1a = p1a->Next;
}
while (p2a) {
//p2a的项数多,将剩余项放入链表
Insert(p, p2a->coe, p2a->exp);
p2a = p2a->Next;
}
p = p->Next;
return p;
}7-2 符号配对
请编写程序检查C语言源程序中下列符号是否配对:/*与*/、(与)、[与]、{与}。
输入格式:
输入为一个C语言源程序。当读到某一行中只有一个句点.和一个回车的时候,标志着输入结束。程序中需要检查配对的符号不超过100个。
输出格式:
首先,如果所有符号配对正确,则在第一行中输出YES,否则输出NO。然后在第二行中指出第一个不配对的符号:如果缺少左符号,则输出?-右符号;如果缺少右符号,则输出左符号-?。
输入样例1:
void test()
{
int i, A[10];
for (i=0; i<10; i++) { /*/
A[i] = i;
}
.
输出样例1:
NO
/*-?
输入样例2:
void test()
{
int i, A[10];
for (i=0; i<10; i++) /**/
A[i] = i;
}]
.
输出样例2:
NO
?-]
输入样例3:
void test()
{
int i
double A[10];
for (i=0; i<10; i++) /**/
A[i] = 0.1*i;
}
.
输出样例3:
YES
鸣谢用户 王渊博 补充数据!
代码长度限制 16 KB
时间限制 400 ms
内存限制 64 MB
参考代码:
#include <stdio.h>
#include <stdlib.h>
#define Maxsize 105
typedef struct StackRecord *Stack;
struct StackRecord {
int top;
char *array;
};
Stack creat();//创建空栈
int cheekEmpty(Stack s);//判断栈是否为空
void push(Stack s, char x);//添加新元素
void pop(Stack s);//删除
char top(Stack s);//取出
char a[100];
char str[200];
int main() {
int i, j = 0, flag = 0;
char ch;
Stack s = creat();
while (gets(str)) {
if (str[0] == '.' && !str[1])
break;
for( i=0; str[i]; i++){
if(str[i]=='('||str[i]=='['||str[i]=='{'||str[i]==')'||str[i]=='}' ||str[i]==']')
a[j++]=str[i];
else if(str[i]=='/'&&str[i+1]=='*'){
a[j++]='<';
i++;
}else if(str[i]=='*'&&str[i+1]=='/'){
a[j++]='>';
i++;
}
}
}
for (i = 0; i < j; i++) {
if (a[i] == '(' || a[i] == '[' || a[i] == '{' || a[i] == '<') {
push(s, a[i]);
} else if (a[i] == ')') {
if (s->top != -1 && top(s) == '(') {
pop(s);
} else {
ch = a[i];
flag = 1;
break;
}
} else if (a[i] == ']') {
if (s->top != -1 && top(s) == '[') pop(s);
else {
ch = a[i];
flag = 1;
break;
}
} else if (a[i] == '}') {
if (s->top != -1 && top(s) == '{') pop(s);
else {
ch = a[i];
flag = 1;
break;
}
} else if (a[i] == '>') {
if (s->top != -1 && top(s) == '<') pop(s);
else {
ch = a[i];
flag = 1;
break;
}
}
}
if (!flag && cheekEmpty(s)) {
printf("YES\n");
} else {
printf("NO\n");
if (!cheekEmpty(s)) {
if (top(s) == '<') printf("/*-?\n");
else printf("%c-?\n", top(s));
} else {
if (ch == '>') printf("?-*/\n");
else printf("?-%c\n", ch);
}
}
return 0;
}
/**
* 创建新栈
* @return
*/
Stack creat() {
Stack s = (Stack) malloc(sizeof(struct StackRecord));
s->top = -1;
s->array = (char *) malloc(sizeof(char) * Maxsize);
return s;
}
/**
* 判断是否为空栈
* @param s
* @return
*/
int cheekEmpty(Stack s) {
if (s->top == -1)
return 1;
else
return 0;
}
/**
*添加元素
* @param s
* @param x
*/
void push(Stack s, char x) {
s->array[++(s->top)] = x;
}
/**
*删除
* @param s
*/
void pop(Stack s) {
s->top--;
}
/**
*取出
* @param s
*/
char top(Stack s) {
return s->array[s->top];
}7-3 银行业务队列简单模拟
设某银行有A、B两个业务窗口,且处理业务的速度不一样,其中A窗口处理速度是B窗口的2倍 —— 即当A窗口每处理完2个顾客时,B窗口处理完1个顾客。给定到达银行的顾客序列,请按业务完成的顺序输出顾客序列。假定不考虑顾客先后到达的时间间隔,并且当不同窗口同时处理完2个顾客时,A窗口顾客优先输出。
输入格式:
输入为一行正整数,其中第1个数字N(≤1000)为顾客总数,后面跟着N位顾客的编号。编号为奇数的顾客需要到A窗口办理业务,为偶数的顾客则去B窗口。数字间以空格分隔。
输出格式:
按业务处理完成的顺序输出顾客的编号。数字间以空格分隔,但最后一个编号后不能有多余的空格。
输入样例:
8 2 1 3 9 4 11 13 15
输出样例:
1 3 2 9 11 4 13 15代码长度限制 16 KB
时间限制 400 ms
内存限制 64 MB
参考代码:
#include <stdio.h>
const int MAX = 1010;
int main() {
int a[MAX], b[MAX], cnta, cntb;
cnta = cntb = 0;
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
int temp;
scanf("%d", &temp);
if (temp % 2) a[++cnta] = temp;
else b[++cntb] = temp;
}
int flag = 0, x = 1, y = 1;
while (x <= cnta || y <= cntb) {
if (x <= cnta) {
if (flag++) printf(" ");
printf("%d", a[x++]);
}
if (x <= cnta) {
if (flag++) printf(" ");
printf("%d", a[x++]);
}
if (y <= cntb) {
if (flag++) printf(" ");
printf("%d", b[y++]);
}
}
return 0;
}
7-4 顺序存储的二叉树的最近的公共祖先问题
设顺序存储的二叉树中有编号为i和j的两个结点,请设计算法求出它们最近的公共祖先结点的编号和值。
输入格式:
输入第1行给出正整数n(≤1000),即顺序存储的最大容量;第2行给出n个非负整数,其间以空格分隔。其中0代表二叉树中的空结点(如果第1个结点为0,则代表一棵空树);第3行给出一对结点编号i和j。
题目保证输入正确对应一棵二叉树,且1≤i,j≤n。
输出格式:
如果i或j对应的是空结点,则输出ERROR: T[x] is NULL,其中x是i或j中先发现错误的那个编号;否则在一行中输出编号为i和j的两个结点最近的公共祖先结点的编号和值,其间以1个空格分隔。
输入样例1:
15
4 3 5 1 10 0 7 0 2 0 9 0 0 6 8
11 4
输出样例1:
2 3
输入样例2:
15
4 3 5 1 0 0 7 0 2 0 9 0 0 6 8
12 8
输出样例2:
ERROR: T[12] is NULL
代码长度限制 16 KB
时间限制 400 ms
内存限制 64 MB
参考代码:
#include <stdio.h>
int find(int i, int j);
/**
* 7-4 顺序存储的二叉树的最近的公共祖先问题
*/
int main() {
int n, i, j, m;
int a[1000];
scanf("%d", &n);
for (i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
scanf("%d %d", &i, &j);
if (a[i] == 0)//查错
{
printf("ERROR: T[%d] is NULL\n", i);
return 0;
}
if (a[j] == 0)//查错
{
printf("ERROR: T[%d] is NULL\n", j);
return 0;
}
m = find(i, j);
printf("%d %d", m, a[m]);
return 0;
}7-5 修理牧场
农夫要修理牧场的一段栅栏,他测量了栅栏,发现需要N块木头,每块木头长度为整数Li个长度单位,于是他购买了一条很长的、能锯成N块的木头,即该木头的长度是Li的总和。
但是农夫自己没有锯子,请人锯木的酬金跟这段木头的长度成正比。为简单起见,不妨就设酬金等于所锯木头的长度。例如,要将长度为20的木头锯成长度为8、7和5的三段,第一次锯木头花费20,将木头锯成12和8;第二次锯木头花费12,将长度为12的木头锯成7和5,总花费为32。如果第一次将木头锯成15和5,则第二次锯木头花费15,总花费为35(大于32)。
请编写程序帮助农夫计算将木头锯成N块的最少花费。
输入格式:
输入首先给出正整数N(≤104),表示要将木头锯成N块。第二行给出N个正整数(≤50),表示每段木块的长度。
输出格式:
输出一个整数,即将木头锯成N块的最少花费。
输入样例:
8
4 5 1 2 1 3 1 1
输出样例:
49代码长度限制 16 KB
时间限制 400 ms
内存限制 64 MB
参考代码:
#include<stdio.h>
#include<stdlib.h>
typedef int ElemType;
typedef struct HuffmanTreeNode {
ElemType data; //哈夫曼树中节点的权值
struct HuffmanTreeNode *left;
struct HuffmanTreeNode *right;
} HuffmanTreeNode, *HuffmanTree;
HuffmanTree createHuffmanTree(ElemType arr[], int N) {
HuffmanTree treeArr[N];
HuffmanTree tree, pRoot = NULL;
for (int i = 0; i < N; i++) { //初始化结构体指针数组,数组中每一个元素为一个结构体指针类型
tree = (HuffmanTree) malloc(sizeof(HuffmanTreeNode));
tree->data = arr[i];
tree->left = tree->right = NULL;
treeArr[i] = tree;
}
for (int i = 1; i < N; i++) { //进行 n-1 次循环建立哈夫曼树
//k1为当前数组中第一个非空树的索引,k2为第二个非空树的索引
int k1 = -1, k2 = 0;
for (int j = 0; j < N; j++) {
if (treeArr[j] != NULL && k1 == -1) {
k1 = j;
continue;
}
if (treeArr[j] != NULL) {
k2 = j;
break;
}
}
//循环遍历当前数组,找出最小值索引k1,和次小值索引k2
for (int j = k2; j < N; j++) {
if (treeArr[j] != NULL) {
if (treeArr[j]->data < treeArr[k1]->data) {//最小
k2 = k1;
k1 = j;
} else if (treeArr[j]->data < treeArr[k2]->data) {//次小
k2 = j;
}
}
}
//由最小权值树和次最小权值树建立一棵新树,pRoot指向树根结点
pRoot = (HuffmanTree) malloc(sizeof(HuffmanTreeNode));
pRoot->data = treeArr[k1]->data + treeArr[k2]->data;
pRoot->left = treeArr[k1];
pRoot->right = treeArr[k2];
treeArr[k1] = pRoot; //将新生成的数加入到数组中k1的位置
treeArr[k2] = NULL; //k2位置为空
}
return pRoot;
}
ElemType calculateWeightLength(HuffmanTree ptrTree, int len) {
if (ptrTree == NULL) { //空树返回0
return 0;
} else {
if (ptrTree->left == NULL && ptrTree->right == NULL) { //访问到叶子节点
return ptrTree->data * len;
} else {
return calculateWeightLength(ptrTree->left, len + 1) + calculateWeightLength(ptrTree->right, len + 1); //向下递归计算
}
}
}
int main() {
ElemType arr[10001];
int i = 0, N;
scanf("%d", &N);
while (i < N)
scanf("%d", &arr[i++]);
HuffmanTree pRoot = createHuffmanTree(arr, N); //返回指向哈夫曼树根节点的指针
printf("%d", calculateWeightLength(pRoot, 0));
return 0;
}7-6 公路村村通
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入格式:
输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
输入样例:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例:
12
参考代码:
#include <stdio.h>
#include <stdlib.h>
int fa[1005];
typedef struct {
int l;
int r;
int weight;
} Node;
Node p[3005];
int n, m, sum, cnt;
int cmp(const void *a, const void *b) {
Node *p1 = (Node *) a;
Node *p2 = (Node *) b;
return p1->weight - p2->weight;
}
int Find(int x) {
return (x == fa[x]) ? (x) : (fa[x] = Find(fa[x]));
}
void Union(int x, int y) {
fa[Find(x)] = Find(y);
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
fa[i] = i;
for (int i = 0; i < m; i++)
scanf("%d %d %d", &p[i].l, &p[i].r, &p[i].weight);
qsort(p, m, sizeof(Node), cmp);
for (int i = 0; i < m; i++) {
if (Find(p[i].l) != Find(p[i].r)) {
sum += p[i].weight;
Union(p[i].l, p[i].r);
cnt++;
}
if (cnt == n - 1)
break;
}
if (cnt == n - 1)
printf("%d\n", sum);
else
printf("-1\n");
return 0;
}7-7 畅通工程之最低成本建设问题
某地区经过对城镇交通状况的调查,得到现有城镇间快速道路的统计数据,并提出“畅通工程”的目标:使整个地区任何两个城镇间都可以实现快速交通(但不一定有直接的快速道路相连,只要互相间接通过快速路可达即可)。现得到城镇道路统计表,表中列出了有可能建设成快速路的若干条道路的成本,求畅通工程需要的最低成本。
输入格式:
输入的第一行给出城镇数目N (1<N≤1000)和候选道路数目M≤3N;随后的M行,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号(从1编号到N)以及该道路改建的预算成本。
输出格式:
输出畅通工程需要的最低成本。如果输入数据不足以保证畅通,则输出“Impossible”。
输入样例1:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例1:
12
输入样例2:
5 4
1 2 1
2 3 2
3 1 3
4 5 4
输出样例2:
Impossible
参考代码:
#include <stdio.h>
#include <stdlib.h>
struct path {
int a, b, c;
} p[3000];
int f[1001], n, m;
void init() {
for (int i = 1; i <= n; i++) f[i] = i;
}
int getf(int k) {
if (f[k] == k) return f[k];
return f[k] = getf(f[k]);
}
int cmp(const void *a, const void *b) {
return ((struct path *) a)->c - ((struct path *) b)->c;
}
int main() {
scanf("%d%d", &n, &m);
init();
for (int i = 0; i < m; i++) {
scanf("%d%d%d", &p[i].a, &p[i].b, &p[i].c);
}
qsort(p, m, sizeof(p[0]), cmp);
int c = 0, ans = 0;
for (int i = 0; i < m; i++) {
if (getf(p[i].a) != getf(p[i].b)) {
ans += p[i].c;
c++;
f[getf(p[i].a)] = getf(p[i].b);
}
}
if (c < n - 1) printf("Impossible\n");
else printf("%d\n", ans);
return 0;
}
7-8 最短工期
一个项目由若干个任务组成,任务之间有先后依赖顺序。项目经理需要设置一系列里程碑,在每个里程碑节点处检查任务的完成情况,并启动后续的任务。现给定一个项目中各个任务之间的关系,请你计算出这个项目的最早完工时间。
输入格式:
首先第一行给出两个正整数:项目里程碑的数量 N(≤100)和任务总数 M。这里的里程碑从 0 到 N−1 编号。随后 M 行,每行给出一项任务的描述,格式为“任务起始里程碑 任务结束里程碑 工作时长”,三个数字均为非负整数,以空格分隔。
输出格式:
如果整个项目的安排是合理可行的,在一行中输出最早完工时间;否则输出"Impossible"。
输入样例 1:
9 12
0 1 6
0 2 4
0 3 5
1 4 1
2 4 1
3 5 2
5 4 0
4 6 9
4 7 7
5 7 4
6 8 2
7 8 4
输出样例 1:
18
输入样例 2:
4 5
0 1 1
0 2 2
2 1 3
1 3 4
3 2 5
输出样例 2:
Impossible
参考代码:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int n, m, ans;
int mp[100][100];
int l[100], q[100], t[100];
int main() {
int a, b, c, head = 0, tail = 0;
scanf("%d%d", &n, &m);
memset(mp, -1, sizeof(mp));
for (int i = 0; i < m; i++) {
scanf("%d%d%d", &a, &b, &c);
mp[a][b] = c;
l[b]++;
}
for (int i = 0; i < n; i++) {
if (!l[i]) {
q[tail++] = i;
}
}
while (head < tail) {
int temp = q[head++];
if (t[temp] > ans) ans = t[temp];
for (int i = 0; i < n; i++) {
if (mp[temp][i] != -1) {
l[i]--;
if (!l[i]) q[tail++] = i;
if (t[i] < t[temp] + mp[temp][i]) {
t[i] = t[temp] + mp[temp][i];
}
}
}
}
if (tail < n) printf("Impossible");
else printf("%d", ans);
}7-9 哈利·波特的考试
哈利·波特要考试了,他需要你的帮助。这门课学的是用魔咒将一种动物变成另一种动物的本事。例如将猫变成老鼠的魔咒是haha,将老鼠变成鱼的魔咒是hehe等等。反方向变化的魔咒就是简单地将原来的魔咒倒过来念,例如ahah可以将老鼠变成猫。另外,如果想把猫变成鱼,可以通过念一个直接魔咒lalala,也可以将猫变老鼠、老鼠变鱼的魔咒连起来念:hahahehe。
现在哈利·波特的手里有一本教材,里面列出了所有的变形魔咒和能变的动物。老师允许他自己带一只动物去考场,要考察他把这只动物变成任意一只指定动物的本事。于是他来问你:带什么动物去可以让最难变的那种动物(即该动物变为哈利·波特自己带去的动物所需要的魔咒最长)需要的魔咒最短?例如:如果只有猫、鼠、鱼,则显然哈利·波特应该带鼠去,因为鼠变成另外两种动物都只需要念4个字符;而如果带猫去,则至少需要念6个字符才能把猫变成鱼;同理,带鱼去也不是最好的选择。
输入格式:
输入说明:输入第1行给出两个正整数N (≤100)和M,其中N是考试涉及的动物总数,M是用于直接变形的魔咒条数。为简单起见,我们将动物按1~N编号。随后M行,每行给出了3个正整数,分别是两种动物的编号、以及它们之间变形需要的魔咒的长度(≤100),数字之间用空格分隔。
输出格式:
输出哈利·波特应该带去考场的动物的编号、以及最长的变形魔咒的长度,中间以空格分隔。如果只带1只动物是不可能完成所有变形要求的,则输出0。如果有若干只动物都可以备选,则输出编号最小的那只。
输入样例:
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
输出样例:
4 70
参考代码:
/**
* 7-9 哈利·波特的考试
* 最短路径 迪杰斯特拉算法
*/
#include<stdio.h>
#include<string.h>
#define maxInt 2147483647
typedef struct {
int arcs[102][102];
int vexnum, arcnum;
} MGraph;
int final[102];//final[w]=1表示求得顶点v0至vw的最短路径
int D[102]; //记录v0到vi的当前最短路径长度
int P[102]; //记录v0到vi的当前最短路径vi的前驱
int i, u, j, m, v, min, w, k, a, b, c, min1 = 999999, max = -991111, p = 0;
void Dijkstra(MGraph G, int v0) {
for (v = 0; v < G.vexnum; v++) //初始化数据
{
final[v] = 0; //全部顶点初始化为未知最短路径状态
D[v] = G.arcs[v0][v];// 将与v0点有连线的顶点加上权值
P[v] = -1; //初始化路径数组P为-1
}
D[v0] = 0; //v0至v0路径为0
final[v0] = 1; // v0至v0不需要求路径
// 开始主循环,每次求得v0到某个v顶点的最短路径
for (v = 1; v < G.vexnum; v++) {
min = maxInt; // 当前所知离v0顶点的最近距离
for (w = 0; w < G.vexnum; w++) // 寻找离v0最近的顶点
{
if (!final[w] && D[w] < min) {
k = w;
min = D[w]; // w顶点离v0顶点更近
}
}
final[k] = 1; // 将目前找到的最近的顶点置为1
for (w = 0; w < G.vexnum; w++) // 修正当前最短路径及距离
{
// 如果经过v顶点的路径比现在这条路径的长度短的话
if (!final[w] && (min + G.arcs[k][w] < D[w])) { // 说明找到了更短的路径,修改D[w]和P[w]
D[w] = min + G.arcs[k][w]; // 修改当前路径长度
P[w] = k;
}
}
}
}
int main() {
MGraph G;
memset(final, 0, sizeof(final));
memset(D, 0x3f3f3f3f, sizeof(D));
memset(G.arcs, 0x3f3f3f3f, sizeof(G.arcs)); //邻接矩阵一定要初始化
scanf("%d %d", &G.vexnum, &m);
for (i = 0; i < m; i++) {
scanf("%d %d %d", &a, &b, &c);
G.arcs[a - 1][b - 1] = c;
G.arcs[b - 1][a - 1] = c;
}
for (u = 0; u < G.vexnum; u++) {
max = -9999999;
Dijkstra(G, u);
for (j = 0; j < G.vexnum; j++) {
if (D[j] > max)
max = D[j];
}
if (max < min1) {
min1 = max;
p = u + 1;
}
}
if (p == 0)
printf("0");
else
printf("%d %d\n", p, min1);
return 0;
}
7-10 旅游规划
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
输入格式:
输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。
输出格式:
在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
输入样例:
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出样例:
3 40
参考代码:
/**
* 7-10 旅游规划
* 最短路径 弗洛伊德算法
*/
#include<stdio.h>
#define MAXN 500
#define ERROR -1
#define Infinite 65534
int N, M, S, D;//城市的个数 高速公路的条数 出发地 目的地
int Dist[MAXN][MAXN], Cost[MAXN][MAXN];//距离与花费矩阵
int dist[MAXN], cost[MAXN], visit[MAXN];//最短距离与花费 标记数组
void Inicialization(void);
void FindTheWay(void);
int FindMinWay(void);
int main() {
scanf("%d %d %d %d", &N, &M, &S, &D);//城市的个数 高速公路的条数 出发地 目的地
Inicialization();//初始化
FindTheWay();
printf("%d %d", dist[D], cost[D]);
return 0;
}
void Inicialization(void) {
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
Dist[i][j] = Cost[i][j] = Infinite;//矩阵初始化为无限值
int v1, v2, d, c;
for (int i = 0; i < M; i++) {
scanf("%d %d %d %d", &v1, &v2, &d, &c);
Dist[v1][v2] = Dist[v2][v1] = d;//输入距离路径
Cost[v1][v2] = Cost[v2][v1] = c;//输入花费路径
}
for (int i = 0; i < N; i++)
dist[i] = cost[i] = Infinite;//矩阵初始化为无限值
}
void FindTheWay(void) {
dist[S] = cost[S] = 0;//出发地为0
visit[S] = 1;//出发地访问标记
int v;
for (int i = 0; i < N; i++)//记录出发地直达的路径
if (!visit[i] && Dist[S][i] < Infinite) //如果没访问 且有路径
{
dist[i] = Dist[S][i];
cost[i] = Cost[S][i];
}
while (1) {
v = FindMinWay();//找出最短出发地直达且未访问的城市
if (v == ERROR) break;
visit[v] = 1;//找出城市的访问标记
for (int i = 0; i < N; i++)//循环每个城市
if (!visit[i] && Dist[v][i] < Infinite)//如果未访问且有路径
if ((dist[v] + Dist[v][i] < dist[i]) ||
(dist[v] + Dist[v][i] == dist[i] && cost[v] + Cost[v][i] < cost[i])) {//如果从先到该城市再到另一城市距离小于直接到另一城市
//或者从先到该城市再到另一城市距离等于直接到另一城市,且花费少
dist[i] = dist[v] + Dist[v][i];//更新最短路径
cost[i] = cost[v] + Cost[v][i];
}
}
}
int FindMinWay(void) {
int min = Infinite;
int temp;
for (int i = 0; i < N; i++)//循环每个城市 找出最短的路径
if (!visit[i] && dist[i] < min) {
min = dist[i];
temp = i;
}
if (min == Infinite) return ERROR;
return temp;
}
7-11 QQ帐户的申请与登陆
实现QQ新帐户申请和老帐户登陆的简化版功能。最大挑战是:据说现在的QQ号码已经有10位数了。
输入格式:
输入首先给出一个正整数N(≤105),随后给出N行指令。每行指令的格式为:“命令符(空格)QQ号码(空格)密码”。其中命令符为“N”(代表New)时表示要新申请一个QQ号,后面是新帐户的号码和密码;命令符为“L”(代表Login)时表示是老帐户登陆,后面是登陆信息。QQ号码为一个不超过10位、但大于1000(据说QQ老总的号码是1001)的整数。密码为不小于6位、不超过16位、且不包含空格的字符串。
输出格式:
针对每条指令,给出相应的信息:
1)若新申请帐户成功,则输出“New: OK”;
2)若新申请的号码已经存在,则输出“ERROR: Exist”;
3)若老帐户登陆成功,则输出“Login: OK”;
4)若老帐户QQ号码不存在,则输出“ERROR: Not Exist”;
5)若老帐户密码错误,则输出“ERROR: Wrong PW”。
输入样例:
5
L 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
L 1234567890 myQQ@qq
L 1234567890 myQQ@qq.com
输出样例:
ERROR: Not Exist
New: OK
ERROR: Exist
ERROR: Wrong PW
Login: OK
参考代码:
/**
* 7-11 QQ帐户的申请与登陆
* 哈希表 分离链接法
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
/*账号与密码最大长度的定义
它们的最大长度需要比题目所给的大一位
这是因为还需要一个位置来储存'\0'来判断字符串的结尾*/
#define Max_Password_Len 17
#define Max_Account_Len 11
#define MaxTableSize 1000000
/*各种状态的定义
最好用正数表示成功的状态
用负数或0表示失败的状态
这样会让强迫症看了舒服一点*/
#define ERROR_WrongPW -2
#define ERROR_Exist -1
#define ERROR_NOTExist 0
#define New_OK 1
#define Login_OK 2
typedef char AccountType[Max_Account_Len];//账号类型定义
typedef char PasswordType[Max_Password_Len];//密码类型定义
typedef int Index;
typedef enum {
New, Log
} Pattern;//两种模式,新建账号与登入账号
typedef struct {
AccountType Account;
PasswordType Password;
} ElemType;//数据类型的定义,每个对应一个用户,内含用户的账号和密码
//链表指针的定义
typedef struct LNode *PtrToLNode;
//链表结点的定义
typedef struct LNode {
PtrToLNode Next;
ElemType Data;
} LNode;
typedef PtrToLNode List;//链表的定义
typedef PtrToLNode Position;//哈希表中结点位置的定义
//哈希表的定义
typedef struct TblNode *HashTable;
typedef struct TblNode {
int TableSize;//哈希表的大小
List Heads;//储存各个列表头节点的数组
} TblNode;
int NextPrime(int N)//返回N的下一个素数
{
int i, P;
P = N % 2 ? N + 2 : N + 1;
//P为N之后的第一个奇数
while (P < MaxTableSize) {
for (i = (int) sqrt(P); i > 2; i--)//因为只考虑奇数,所以i为2时就结束了
if (P % i == 0)
break;
if (i == 2)
break;//i为2说明P为素数
else
P += 2;//i!=2说明P不是素数,则P指向下一个奇数
}
return P;
}
int Hash(int Key, int TableSize) {//返回Key值相对应的哈希值,即其在哈希表中的储存下标
return Key % TableSize;
}
HashTable CreateTable(int TableSize) { //构造空的哈希表
HashTable H;
int i;
H = (HashTable) malloc(sizeof(TblNode));
H->TableSize = NextPrime(TableSize);
H->Heads = (List) malloc(sizeof(LNode) * H->TableSize);
for (i = 0; i < H->TableSize; i++) {
H->Heads[i].Data.Account[0] = '\0';
H->Heads[i].Data.Password[0] = '\0';
H->Heads[i].Next = NULL;
}
return H;
}
Position Find(HashTable H, ElemType Key) {
Position Pos;
Index p;
if (strlen(Key.Account) > 5) //账号大于5位时取最后5位
p = Hash(atoi(Key.Account +
strlen(Key.Account) - 5), H->TableSize);
else//账号不大于5位则等于它本身
p = Hash(atoi(Key.Account), H->TableSize);
Pos = H->Heads[p].Next;
while (Pos && strcmp(Key.Account, Pos->Data.Account))
Pos = Pos->Next;
return Pos;//Pos指向用户数据的位置,没有注册就返回NULL
}
int NewOrLog(HashTable H, ElemType Key, Pattern P) { //返回状态参数
Position Pos, NewPos;
Index p;
Pos = Find(H, Key);
switch (P) {
case Log:
if (Pos == NULL)
return ERROR_NOTExist;//登陆时不存在账号
else if (strcmp(Pos->Data.Password, Key.Password) ||
(strlen(Key.Password) > 16 || strlen(Key.Password) < 6))
return ERROR_WrongPW; //密码错误或格式错误
else
return Login_OK;//账号和密码均正确,可以登录
case New:
if (Pos != NULL)
return ERROR_Exist; //新建账号时发现已经存在这样的账号了
else {
NewPos = (Position) malloc(sizeof(LNode));
strcpy(NewPos->Data.Account, Key.Account);
strcpy(NewPos->Data.Password, Key.Password);
if (strlen(Key.Account) > 5)
p = Hash(atoi(Key.Account +
strlen(Key.Account) - 5), H->TableSize);
else
p = Hash(atoi(Key.Account), H->TableSize);
NewPos->Next = H->Heads[p].Next;
H->Heads[p].Next = NewPos;
return New_OK; //插入新值并返回插入成功
}
}
}
void DestroyTable(HashTable H) { //销毁哈希表
PtrToLNode p, q;
int i;
for (i = 0; i < H->TableSize; i++) {
q = H->Heads[i].Next;
while (q) {
p = q->Next;
free(q);
q = p;
}
}
free(H);
}
int main(void) {
int N, i;
ElemType Key;
char Input;
Pattern P;
HashTable H;
scanf("%d", &N);
H = CreateTable(2 * N);
for (i = 0; i < N; i++) {
scanf("\n%c %s %s", &Input, Key.Account, Key.Password);
P = (Input == 'L') ? Log : New;
switch (NewOrLog(H, Key, P)) {//最后根据不同返回值输出对应状态即可
case ERROR_Exist:
printf("ERROR: Exist\n");
break;
case ERROR_NOTExist:
printf("ERROR: Not Exist\n");
break;
case ERROR_WrongPW:
printf("ERROR: Wrong PW\n");
break;
case Login_OK:
printf("Login: OK\n");
break;
case New_OK:
printf("New: OK\n");
break;
}
}
DestroyTable(H);
return 0;
}
7-12 人以群分
社交网络中我们给每个人定义了一个“活跃度”,现希望根据这个指标把人群分为两大类,即外向型(outgoing,即活跃度高的)和内向型(introverted,即活跃度低的)。要求两类人群的规模尽可能接近,而他们的总活跃度差距尽可能拉开。
输入格式:
输入第一行给出一个正整数N(2≤N≤105)。随后一行给出N个正整数,分别是每个人的活跃度,其间以空格分隔。题目保证这些数字以及它们的和都不会超过231。
输出格式:
按下列格式输出:
Outgoing #: N1
Introverted #: N2
Diff = N3
其中N1是外向型人的个数;N2是内向型人的个数;N3是两群人总活跃度之差的绝对值。
输入样例1:
10
23 8 10 99 46 2333 46 1 666 555
输出样例1:
Outgoing #: 5
Introverted #: 5
Diff = 3611
输入样例2:
13
110 79 218 69 3721 100 29 135 2 6 13 5188 85
输出样例2:
Outgoing #: 7
Introverted #: 6
Diff = 9359
参考代码:
/**
* 7-12 人以群分
* 排序
*/
#include <stdio.h>
#include <stdlib.h>
int comfunc(const void *elem1, const void *elem2);
void sort_character(int *p, int n);
int main() {
int n, i;
int a[100001];
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%d", &a[i]);
qsort(a, n, sizeof(int), comfunc);
sort_character(a, n);
return 0;
}
int comfunc(const void *elem1, const void *elem2) {
int *p1 = (int *) elem1;
int *p2 = (int *) elem2;
return *p1 - *p2;
}
void sort_character(int *p, int n) {
int i, j, n1, n2, sum1, sum2, dif, dif1, dif2;
sum1 = sum2 = 0;
dif = dif1 = dif2 = 0;
if (n % 2 == 0) {
n1 = n2 = n / 2;
for (i = 0; i < n1; i++)
sum1 += p[i];
for (i = n1; i < n; i++)
sum2 += p[i];
dif = abs(sum2 - sum1);
} else {
n1 = n2 = n / 2;
for (i = 0; i < n1; i++)
sum1 += p[i];
for (i = n / 2 + 1; i < n; i++)
sum2 += p[i];
dif1 = abs(sum1 + p[n1] - sum2);
dif2 = abs(sum2 + p[n2] - sum1);
dif = (dif1 > dif2) ? dif1 : dif2;
if (dif1 > dif2)
n1++;
else
n2++;
}
printf("Outgoing #: %d\n", n2);
printf("Introverted #: %d\n", n1);
printf("Diff = %d\n", dif);
}
7-13 寻找大富翁
胡润研究院的调查显示,截至2017年底,中国个人资产超过1亿元的高净值人群达15万人。假设给出N个人的个人资产值,请快速找出资产排前M位的大富翁。
输入格式:
输入首先给出两个正整数N(≤106)和M(≤10),其中N为总人数,M为需要找出的大富翁数;接下来一行给出N个人的个人资产值,以百万元为单位,为不超过长整型范围的整数。数字间以空格分隔。
输出格式:
在一行内按非递增顺序输出资产排前M位的大富翁的个人资产值。数字间以空格分隔,但结尾不得有多余空格。
输入样例:
8 3
8 12 7 3 20 9 5 18
输出样例:
20 18 12
参考代码:
/**
* 7-13 寻找大富翁
* 堆排序和选择排序
*/
#include <stdio.h> //堆排序; 注意:此算法中,下标从1开始
#define max 1000010
int num[max];
void sift(int *num, int low, int high) //将下标为low位置上的点调到适当位置
{
int i, j, temp;
i = low;
j = 2 * i; //num[j]是num[i]的左孩子结点;
temp = num[i]; //待调整的结点
while (j <= high) {
if (j < high && num[j] < num[j + 1]) //如果右孩子比较大,则把j指向右孩子,j变为2*i+1;
++j;
if (temp < num[j]) {
num[i] = num[j]; //将num[j]调整到双亲结点的位置上;
i = j; //修改i和j的值,以便继续向下调整;
j = i * 2;
} else break; //调整结束;
}
num[i] = temp; //被调整的结点放入最终位置
}
int main() {
int n, m, i, temp, count = 0;
scanf("%d%d", &n, &m);
for (i = 1; i <= n; i++)
scanf("%d", &num[i]);
if (n < m) m = n; //注意,有一个测试点是n小于m的情况,这时,只用排前n个;
for (i = n / 2; i >= 1; i--) //所有结点建立初始堆
sift(num, i, n);
for (i = n; i >= 2; i--) //进行n-1次循环,完成堆排序
{
/*以下3句换出了根节点中的关键字,将其放入最终位置*/
temp = num[1];
num[1] = num[i];
num[i] = temp;
count++;
if (count == 1)
printf("%d", num[i]);
else
printf(" %d", num[i]);
if (count == m) break; //打印前m个;
sift(num, 1, i - 1); //减少了1个关键字的无序序列,继续调整。
}
if (m == n) printf(" %d", num[1]); //当n<m的特殊情况下,上面只打印了n~2,还有最后一个下标为1的没有打印,故再打印一个。
return 0;
}7-14 PAT排名汇总
计算机程序设计能力考试(Programming Ability Test,简称PAT)旨在通过统一组织的在线考试及自动评测方法客观地评判考生的算法设计与程序设计实现能力,科学的评价计算机程序设计人才,为企业选拔人才提供参考标准(网址http://www.patest.cn)。
每次考试会在若干个不同的考点同时举行,每个考点用局域网,产生本考点的成绩。考试结束后,各个考点的成绩将即刻汇总成一张总的排名表。
现在就请你写一个程序自动归并各个考点的成绩并生成总排名表。
输入格式:
输入的第一行给出一个正整数N(≤100),代表考点总数。随后给出N个考点的成绩,格式为:首先一行给出正整数K(≤300),代表该考点的考生总数;随后K行,每行给出1个考生的信息,包括考号(由13位整数字组成)和得分(为[0,100]区间内的整数),中间用空格分隔。文章来源:https://www.toymoban.com/news/detail-496168.html
输出格式:
首先在第一行里输出考生总数。随后输出汇总的排名表,每个考生的信息占一行,顺序为:考号、最终排名、考点编号、在该考点的排名。其中考点按输入给出的顺序从1到N编号。考生的输出须按最终排名的非递减顺序输出,获得相同分数的考生应有相同名次,并按考号的递增顺序输出。文章来源地址https://www.toymoban.com/news/detail-496168.html
输入样例:
2
5
1234567890001 95
1234567890005 100
1234567890003 95
1234567890002 77
1234567890004 85
4
1234567890013 65
1234567890011 25
1234567890014 100
1234567890012 85
输出样例:
9
1234567890005 1 1 1
1234567890014 1 2 1
1234567890001 3 1 2
1234567890003 3 1 2
1234567890004 5 1 4
1234567890012 5 2 2
1234567890002 7 1 5
1234567890013 8 2 3
1234567890011 9 2 4
参考代码:
/**
* 7-14 PAT排名汇总
* 快速排序
*/
#include <stdio.h>
#include <string.h>
struct stu {
char id[14]; //考号
int score; //分数
int kc; //考场
};
struct stu a[30000];
int bigger(const char *s1, const char *s2) {
for (int i = 0; i < 13; i++)
if (s1[i] > s2[i])
return 1;
else if (s1[i] < s2[i])
return 0;
return 1;
}
void qsort(int l, int r) {
if (l >= r)
return;
int i = l;
int j = r;
struct stu t = a[l];
while (i != j) {
while (i < j && (a[j].score < t.score || a[j].score == t.score && bigger(a[j].id, t.id)))
j--;
while (i < j && (a[i].score > t.score || a[i].score == t.score && bigger(t.id, a[i].id)))
i++;
if (i < j) {
struct stu s = a[i];
a[i] = a[j];
a[j] = s;
}
}
a[l] = a[i];
a[i] = t;
qsort(l, i - 1);
qsort(i + 1, r);
return;
}
void Copy(int *b2, int *b1, int n) {
for (int i = 1; i <= n; i++)
b2[i] = b1[i];
}
int main() {
int n, j, i, top = 0;
scanf("%d", &n);
for (i = 1; i <= n; i++) {
int k;
scanf("%d", &k);
for (j = 0; j < k; j++) {
char id[14];
int score;
scanf("%s %d", id, &score);
a[top].score = score;
a[top].kc = i;
strcpy(a[top].id, id);
top++;
}
}
qsort(0, top - 1);
int levall = 1, b1[n + 1], b2[n + 1], score = a[0].score;
for (i = 1; i <= n; i++)
b1[i] = 1, b2[i] = 1;
printf("%d\n", top);
printf("%s %d %d %d\n", a[0].id, 1, a[0].kc, 1);
int llevall = 1; //上一个总排名
levall = 2; //总排名
Copy(b2, b1, n);
b1[a[0].kc]++;
for (i = 1; i < top; i++) {
if (a[i].score == a[i - 1].score) {
printf("%s %d %d %d\n", a[i].id, llevall, a[i].kc, b2[a[i].kc]);
levall++;
b1[a[i].kc]++;
} else {
printf("%s %d %d %d\n", a[i].id, levall, a[i].kc, b1[a[i].kc]);
llevall = levall;
levall++;
Copy(b2, b1, n);
b1[a[i].kc]++; //考场的排名
}
}
return 0;
}到了这里,关于郑州轻工业大学2022-2023(2)数据结构题目集的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!