二叉树与树、森林之间的转换-Toy模板网

这篇具有很好参考价值的文章主要介绍了二叉树与树、森林之间的转换。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

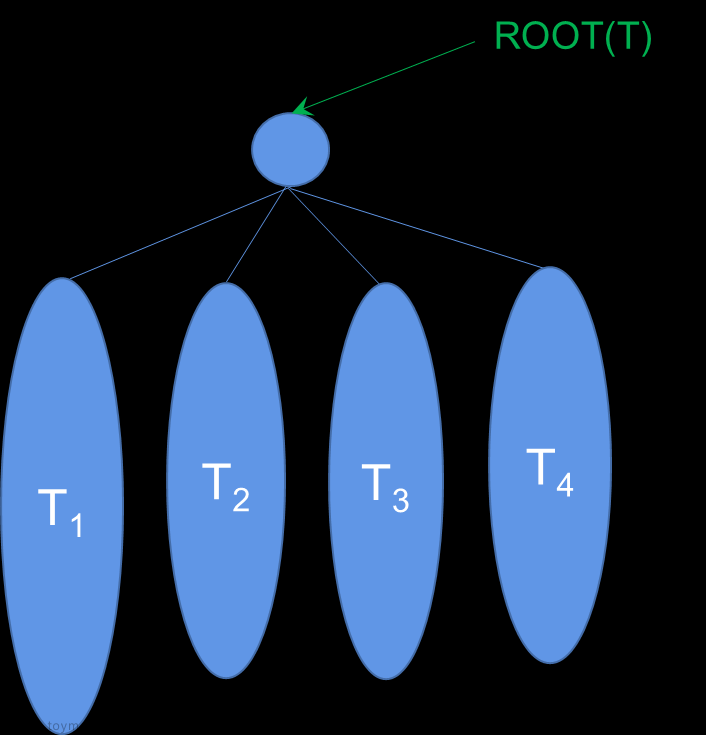
关于树的概念

树可以称为特殊的森林，其中二叉树是树中一些节点度数最大为2 ，并且分左右孩子的树

● 二叉树很重要

• 结构简单

• 存储效率高

• 运算算法相对简单

• 任何森林、树都可以转换成二叉树

● 讨论

• 二叉树 == 度为2 的树 ?

答: 树的度就是树节点数, 最大的度数 , 一般的树的两个孩子节点 ,是不区分左右孩子的 , 而二叉树是区分左右孩子的 , 所以如果一个树区分左右孩子 , 那就是二叉树

如果一个树, 虽然度数最大为 2 , 但是不区分左右孩子就不是二叉树.

森林、树转换成二叉树

二叉树与树、森林之间的转换

我们先思考，为什么要把森林转换成二叉树，二叉树有什么好处，再思考如何转换？

因为二叉树具有它独特的特点和重要的性质。转化为二叉树可以使复杂的问题简单化。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个结点最多只能有两棵子树，且有左右之分。森林转化为二叉树，更多的是为了对森林中的节点做遍历操作。

知乎回答：

我的理解是普通的树状结构自带的特点太少，而二叉树有很多其自身特点比如满二叉树每层的节点个数是确定，总节点个数个数确定了，其边的个数也就确定了，还有很多已经研究明白的性质，在具体的实际问题中抽象出来的树状结构可能并不是二叉树，如果针对么个树状结构提供一套解决方案那么树状结构不同，代码会有差异，而此时，如果把通用的树状结构转换为二叉树，就可以使用已经研究明白的二叉树的性质解决问题了。

二叉树类似一个规整的数据结构，而实际问题中抽象出来的数据结构可以转换为这个规整的数据结构，通过二叉树解决问题的途径和方法更丰富，所以会把树、森林转换为二叉树。

作者：凌夜知惜
链接：https://www.zhihu.com/question/288101803/answer/2584131494
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

转换方法：

（1）在所有相邻兄弟节点（森林中每棵树的根节点可看成兄弟节点）之间加一水平连线。

（2）兄弟们只留一个老大，其余兄弟和双亲断开联系 ,靠老大和双亲联系，从多接口变成单接口。

对每个非叶节点 k ,除了其最左边的孩子节点外,删去 k 与其他孩子节点的连线

(最左孩子仍作为左孩子)

(3)为了层次设计 , 左孩子仍为左孩子 , 右边的兄弟旋转变成左边兄弟的右孩子

所有水平线段以左边节点为轴心顺时针旋转45度(兄弟作为右孩子)

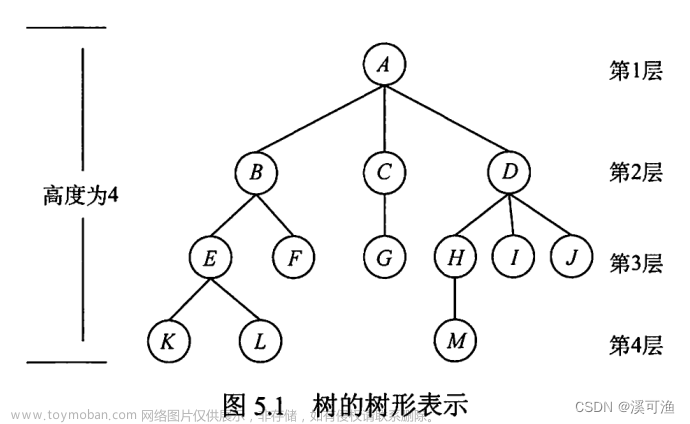
我们依次旋转，第一个树，我们以 B 为旋钮，然后 c 成为 B 的右孩子，D成为 c的右孩子

第二棵树，根节点 E 是 A的兄弟，成为 A 的右孩子，E的唯一一个孩子成为左孩子

第三棵树，根节点 G 是 E 的兄弟，成为 E 的右孩子， G的左孩子H 依然是G的左孩子

I 作为 H 的兄弟，成为 H 的右孩子

总结：

在任何一棵树里面，把最左的孩子仍然作为左孩子去使用，而把它所有的兄弟作为右孩子，通过这样的转换，我们把森林转换成了二叉树。

二叉树还原为森林、树

我们怎样将二叉树，转换为森林或树呢？我们怎么把森林转换成二叉树的，就怎么转换回去即可

我们知道，森林转换成二叉树，二叉树所有节点的右孩子，转换前，是其此节点的兄弟，左孩子仍为其左孩子，

所以我们只需要将左孩子仍然保留，右孩子转换成其双亲的兄弟，变成兄弟后，再指向老大的双亲即可，没有双亲就分散成森林即可。

下面我们开始实操：

（1）对于一棵二叉树中任一节点K1,沿着k₁的右子树方向搜索所有右孩子节点，得节点序列

k₂，k₃，.....，kₘ，其中k ᵢ₊₁ 为k ᵢ的右孩子节点（1<= i < m）, kₘ 没有右孩子节点。

（2）删去k₁ ， k₂，。。。，kₘ 之间连线。（找到变成兄弟的右孩子的节点，断开束缚）

（3）若 k₁ 有双亲节点 k , 则连接 k 与 k ᵢ (2<= i <= m) (兄弟根据老大找妈妈，没有则独立)

（4）将图形规整化，使各节点按层次排列。

这样我们就实现了二叉树转换成森林、树的方法

其实在这样的转换过程里面，是把原先的保留左孩子的关系仍然保留，而原有的兄弟是他的右子树上的节点，现在我们要二叉树转换回来，就要把原有的右子树上的链条去掉，再次把右子树上的节点，恢复成兄弟关系，然后兄弟指向双亲即可。文章来源地址https://www.toymoban.com/news/detail-496736.html