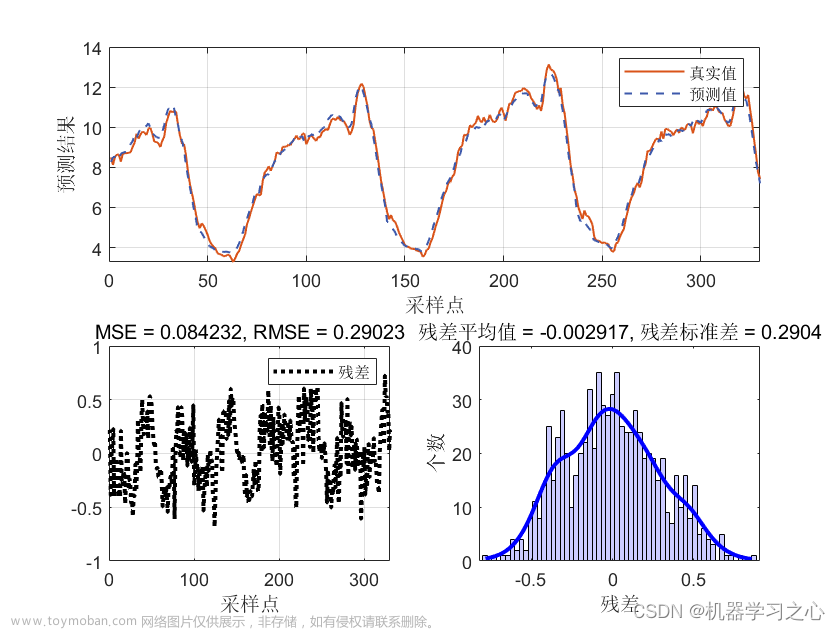
1.AR参数谱估计理论
自回归模型（AR模型）：现在的输出是现在的输入和过去p个输出的加权和，即
AR模型的参数
与
的自相关函数
的关系:
写成矩阵形式：
(上面两式为AR模型的正则方程或Yule-Walker方程)
1.1 Levinson-Durbin算法
参数说明：
为p阶AR模型在阶次为m时的第k个系数，
为m阶的前向预测的最小误差功率，km（即
）为反射系数,表示第m阶时的第m个系数。
算法步骤如下：
（1）给定
和阶次p,求出
的自相关函数
（2）计算
和
（3）由Levinson-Durbin递推算法求
、
和
（其中m=1,…,p）从而得到p阶时的参数
, 
,…, 
和
，即
（4）求功率谱
1.2 pburg算法
参数说明：
为前向预测误差，
为后向预测误差
算法步骤如下：
（1）初始化
和
并求出
，即
（2）求反射系数并更新前向和后向预测误差，即
其中m=1,2,…,p
（3）求a1(1)和ρ1，即
（4）由Levinson递推算法求
和
（其中m=1,…,p）从而得到p阶时的参数
, 
,…, 
和
，即
（5）求功率谱
2.仿真分析
2.1 Levinson-Durbin算法仿真
function [ap,E]=Levinson_Durbin(x,p)
rx=xcorr(x,'biased');%求x(n)的自相关函数
rxm=zeros(1,p+1);%索引从1开始，用rxm(1)-rxm(p+1)表示rx(0)-rx(p)
N=length(x);
for i=1:p+1
rxm(i)=rx(N+i-1);
end
%当阶次m=1时，先求出a1(1)和ρ1
a=zeros(p,p); %p阶AR模型在阶次为m时的系数
rho=zeros(1,p);%前向预测的最小误差功率ρ
a(1,1)=-rxm(2)/rxm(1);%求出a1(1)
rho(1)=rxm(1)*(1-(a(1,1))^2);
%Levinson-Durbin递推
k=zeros(1,p);%反射系数
k(1)=a(1,1);
for m=2:p
a(m,m)=-rxm(m+1)/rho(m-1);
for i=1:m-1
a(m,m)=a(m,m)-(a(m-1,i)*rxm(m+1-i))/rho(m-1);
end
k(m)=a(m,m);%求反射系数km(km=am(m)),且|km|<1
if (k(m)>=1)
break;
end
for i=1:m-1
a(m,i)=a(m-1,i)+k(m)*a(m-1,m-i);
end
rho(m)=rho(m-1)*(1-(k(m))^2);
end
%求阶次为p时的系数
ap=zeros(1,p);
for k=1:p
ap(k)=a(p,k);
end
%p阶时最小预测误差功率
E=rho(p);2.2 pburg算法仿真
function [ap,E]=p_burg(x,p)
N=length(x);
ef=zeros(p,N);%前向预测误差
eb=zeros(p,N);%后向预测误差
k=zeros(1,p);%反射系数
rho=zeros(1,p);%预测误差功率
a=zeros(p,p);
ef(1,:)=x;eb(1,:)=x;%初始化ef和eb
rx0=(1/N)*sum(abs(x).^2);%求rx(0)
%求反射系数km
for m=1:p
sum1=0;
sum2=0;
for n=m+1:N
sum1=sum1+ef(m,n)*eb(m,n-1);
sum2=sum2+(abs(ef(m,n)).^2)+(abs(eb(m,n-1)).^2);
end
k(m)=-(2*sum1)/sum2;
if (k(m)>=1)
break;
end
for n=m+1:N %更新前向和后向预测误差
ef(m+1,n)=ef(m,n)+k(m)*eb(m,n-1);
eb(m+1,n)=eb(m,n-1)+k(m)*ef(m,n);
end
end
a(1,1)=k(1);%求a1(1)
rho(1)=(1-abs(k(1)).^2)*rx0;%求ρ1
%估计出km后，在阶次m时的AR模型系数由Levinson算法递推求出
for m=2:p
a(m,m)=k(m);
for i=1:m-1
a(m,i)=a(m-1,i)+k(m)*a(m-1,m-i);
end
rho(m)=(1-abs(k(m)).^2)*rho(m-1);
end
%求阶次为p时的系数
ap=zeros(1,p);
for i=1:p
ap(i)=a(p,i);
end
%p阶时最小预测误差功率
E=rho(p);
2.3 与MATLAB内部函数对比
clear
Fs=1000;%采样频率
f1=150;f2=300;f3=310;
N=1024;%1024点序列
n=0:N-1;
t=n/Fs;%采用的时间序列
x=cos(2*pi*f1*t)+cos(2*pi*f2*t)+2*cos(2*pi*f3*t)+randn(size(n));
p=60;%阶次p
[ap1,E1]=Levinson_Durbin(x,p);%调用自己编写的Levinson算法估计AR模型参数
%求功率谱
[H1,w1]=freqz(sqrt(E1),[1,ap1],N);
Px1=abs(H1).^2;f1=w1/(2*pi);
Px1=Px1/max(Px1);Px1=10*log10(Px1);
figure(1)
subplot(311)
plot(f1,Px1);title('自己编写的Levinson-Durbin算法参数谱估计');
[a2,E2]=aryule(x,p);%调用matlab内部函数估计AR模型参数
%求功率谱
[H2,w2]=freqz(sqrt(E2),a2,N);
Px2=abs(H2).^2;f2=w2/(2*pi);
Px2=Px2/max(Px2);Px2=10*log10(Px2);
subplot(312)
plot(f2,Px2);title('matlab内部函数参数谱估计');
[Pxx,F1]=pyulear(x,p,N,Fs);%直接调用matlab中的pyulear函数估计功率谱
Pxx=10*log10(Pxx);
subplot(313)
plot(F1/Fs,Pxx);title('直接调用matlab中的pyulear函数估计功率谱');
[ap3,E3]=p_burg(x,p);%调用自己编写的pburg算法估计AR模型参数
%求功率谱
[H3,w3]=freqz(sqrt(E3),[1,ap3],N);
Px3=abs(H3).^2;f3=w3/(2*pi);
Px3=Px3/max(Px3);Px3=10*log10(Px3);
figure(2)
subplot(311)
plot(f3,Px3);title('自己编写的pburg算法参数谱估计')
[a4,E4]=arburg(x,p);%调用matlab内部函数估计AR模型参数
%求功率谱
[H4,w4]=freqz(sqrt(E4),a4,N);
Px4=abs(H4).^2;f4=w4/(2*pi);
Px4=Px4/max(Px4);Px4=10*log10(Px4);
subplot(312)
plot(f4,Px4);title('matlab内部函数参数谱估计');
[Pxxx,F2]=pburg(x,p,N,Fs);%直接调用matlab中的pburg估计功率谱
Pxxx=10*log10(Pxxx);
subplot(313)
plot(F2/Fs,Pxxx);title('直接调用matlab中的pburg估计功率谱');
2.4 仿真结果分析
2.4.1 Levinson-Durbin算法仿真结果
文章来源：https://www.toymoban.com/news/detail-496762.html
2.4.2 pburg算法仿真结果
文章来源地址https://www.toymoban.com/news/detail-496762.html
到了这里，关于AR参数谱估计(含MATLAB代码)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
