【人工智能】— 无监督学习、K-means聚类（K-means clustering）、K-means损失函数，目标函数-Toy模板网

这篇具有很好参考价值的文章主要介绍了【人工智能】— 无监督学习、K-means聚类（K-means clustering）、K-means损失函数，目标函数。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

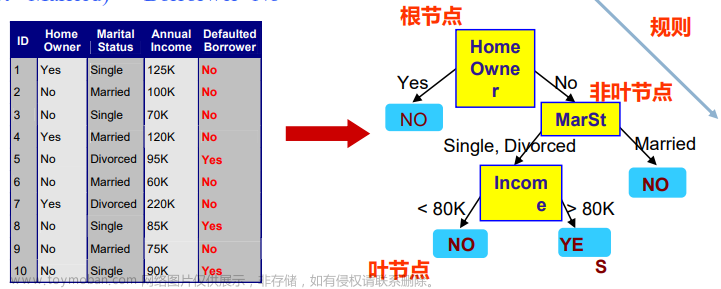
无监督学习

无监督学习是指在没有标签的数据上进行学习，即没有监督信号的指导下进行模型训练。在无监督学习中，我们主要关注从无标签数据中学习出数据的低维结构和隐藏的模式。

通过无标签数据，我们可以预测以下内容：

低维结构：通过无监督学习算法如主成分分析（PCA），我们可以发现数据中的主要变化方向和低维表示，帮助我们理解数据的内在结构和进行数据降维。
集群结构：通过聚类算法如K均值聚类或层次聚类，我们可以将无标签数据划分为不同的组或类别，从而发现数据中的集群结构。
关联规则：通过关联规则挖掘算法如Apriori算法或FP-growth算法，我们可以发现数据中的频繁项集和关联规则，揭示不同特征之间的关联关系。

聚类（Clustering）

• 将数据对象分组为子集或“簇”：

簇内具有高相似性
簇间具有低相似性

• 聚类是一项常见而重要的任务，在科学、工程、信息科学和其他领域中都有广泛的应用：

对具有相同功能的基因进行分组
对具有相似政治观点的个体进行分组
对具有相似主题的文档进行分类
从图片中识别相似的对象

【人工智能】— 无监督学习、K-means聚类（K-means clustering）、K-means损失函数，目标函数

输入：输入点的训练集
输出：将每个点分配到一个簇中
其中 $Dtrain = \{x1, ..., xn\}$ 为输入点的训练集
$(C (1), ..., C (n))$ 为将每个点分配到的簇，其中 $C (i)$ 属于 ${1, ..., k\}$ 表示第 i 个点所属的簇。

K-means聚类（K-means clustering）

K-means的目标是最小化所有数据点与其所属簇中心点之间的欧氏距离的平方和。

K-means的算法过程如下：

随机选择K个初始簇中心点（质心）。
将每个数据点分配到与其最近的簇中心点所对应的簇。
更新每个簇的中心点为该簇中所有数据点的平均值。
重复步骤2和步骤3，直到簇中心点不再发生明显变化或达到预定的迭代次数。

K-means损失函数

$\textbf{x}$ 为样本， $μ_{C(j)}$ 表示某个簇 $C (j)$ 的中心，
下式表示将 $x_j$ 分到 $C (j)$ 这个簇上时，到簇中心 $μ_{C(j)}$ 的欧式距离求和
【人工智能】— 无监督学习、K-means聚类（K-means clustering）、K-means损失函数，目标函数

目标函数

找到如何划分簇 $C$ 、如何选择簇中心 $μ$ ，使得每个簇的样本到簇中心的欧氏距离和最小
【人工智能】— 无监督学习、K-means聚类（K-means clustering）、K-means损失函数，目标函数

策略：交替最小化

步骤1：如果知道聚类中心，可以找到最佳 $C$
- 固定 $μ$ ，优化 $C$
  
  将每个点指定给最近的聚类中心
步骤2：如果知道集簇分配 $C$ ，可以找到最好的聚类中心 $μ$ 文章来源地址https://www.toymoban.com/news/detail-496999.html
- 固定 $C$ ，优化 $μ$
  
  解决方案：第 $i$ 个簇中选择该簇所有点的平均值重新作为簇中心，正好是步骤2（重新选择聚类中心）