神经网络：损失函数-Toy模板网

这篇具有很好参考价值的文章主要介绍了神经网络：损失函数。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

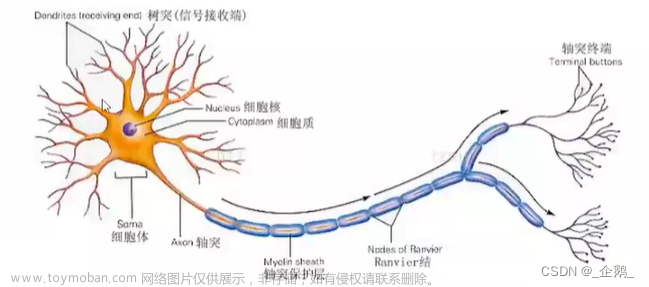
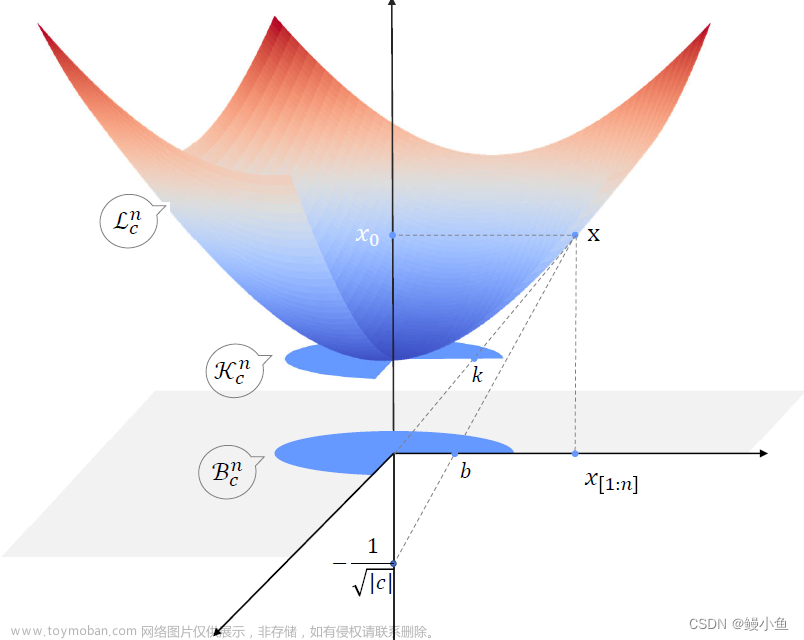
在计算机视觉中，损失函数（Loss Function）用于衡量预测结果与真实标签之间的差异，是神经网络训练中的重要组成部分。损失函数的作用、原理和意义如下所述：

作用：

衡量模型预测结果与真实标签之间的差异，反映模型的性能。
提供一个可优化的目标函数，通过最小化损失函数来优化模型参数。

原理：

损失函数基于预测值和真实值之间的差异进行定义。它是一个标量函数，将预测值和真实值作为输入，并输出一个数值作为模型的损失。常见的损失函数包括均方误差（Mean Squared Error，MSE）、交叉熵损失（Cross-Entropy Loss）、KL 散度（Kullback-Leibler Divergence）等。

意义：

损失函数在训练过程中衡量模型的性能，指导模型参数的更新。通过最小化损失函数，可以提高模型的准确性和泛化能力。
损失函数的选择与具体的任务相关。不同的损失函数适用于不同的问题，可以根据问题的性质和要求选择合适的损失函数。

从数学角度解释损失函数：

假设预测结果为 $\hat{y}$ ，真实标签为 $y$ ，损失函数为 $L(\hat{y}, y)$ 。
损失函数的具体形式根据任务的不同而定。以均方误差（MSE）为例，其数学表达式为：
$L(\hat{y}, y) = \frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i)^2$
其中， $n$ 表示样本数量， $\hat{y}_i$ 表示第 $i$ 个样本的预测值， $y_i$ 表示第 $i$ 个样本的真实标签。
损失函数衡量预测值和真实值之间的差异程度。损失越小表示预测结果越接近真实标签，损失越大表示预测结果与真实标签之间差异较大。
在模型训练过程中，通过反向传播算法计算损失函数对模型参数的梯度，并使用优化算法（如梯度下降）更新模型参数，以最小化损失函数。

总之，损失函数在计算机视觉中起着至关重要的作用，它衡量了模型的性能并提供了优化目标，帮助模型学习从输入数据中提取有用的特征，使得模型能够更好地进行预测和分类任务。

常见的损失函数在计算机视觉中包括以下几种：

均方误差（Mean Squared Error，MSE）：
- 数学表达式：
  $L(\hat{y}, y) = \frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i)^2$
  $\hat{y}_i$ ：模型的预测值（第 $i$ 个样本）
  $y_i$ ：真实标签值（第 $i$ 个样本）
  $n$ ：样本数量
- 优点：对异常值敏感，梯度下降速度较快。
- 缺点：容易受到离群值的影响，可能导致较大的梯度更新。
- 适用场景：回归问题，例如人脸关键点检测、目标检测中的边界框回归。
交叉熵损失（Cross-Entropy Loss）：
- 数学表达式：
  $L(\hat{y}, y) = -\frac{1}{n} \sum_{i=1}^{n} y_i \log(\hat{y}_i)$
  $\hat{y}_i$ ：模型的预测概率值（第 $i$ 个样本）
  $y_i$ ：真实标签的独热编码（第 $i$ 个样本）
  $n$ ：样本数量
- 优点：适用于分类问题，鼓励模型对正确类别的预测概率趋近于1。
- 缺点：可能存在梯度饱和问题，对类别不平衡敏感。
- 适用场景：分类问题，例如图像分类、目标识别中的分类任务。
KL 散度（Kullback-Leibler Divergence）：
- 数学表达式：
  $L(\hat{y}, y) = \sum_{i=1}^{n} y_i \log\left(\frac{y_i}{\hat{y}_i}\right)$
  $\hat{y}_i$ ：模型的预测概率值（第 $i$ 个样本）
  $y_i$ ：真实概率分布的概率值（第 $i$ 个样本）
  $n$ ：样本数量
- 优点：度量两个概率分布之间的差异。
- 缺点：不是对称的，对异常值敏感。
- 适用场景：生成模型、无监督学习中的概率分布匹配问题。
Hinge Loss：
- 数学表达式：
- $L(\hat{y}, y) = \max(0, 1 - \hat{y} \cdot y)$
- $\hat{y}$ ：模型的预测结果（标量）
- $y$ ：真实标签（1 或 -1）
- 优点：适用于支持向量机（SVM）和最大间隔分类问题，鼓励模型将正负样本分开。
- 缺点：不连续可导，可能存在类别不平衡问题。
- 适用场景：支持向量机（SVM）、二分类问题中的最大间隔分类。

以上是常见的损失函数及其数学表达式、优缺点和适用场景。在实际应用中，可以根据具体问题和任务的特点选择合适的损失函数。

以下是在PyTorch中使用上述损失函数的代码示例：文章来源地址https://www.toymoban.com/news/detail-497109.html

import torch
import torch.nn as nn

# 定义预测值和真实标签
y_pred = torch.tensor([0.9, 0.2, 0.4])  # 预测值
y_true = torch.tensor([1, 0, 1])       # 真实标签

# 均方误差损失函数
mse_loss = nn.MSELoss()
mse = mse_loss(y_pred, y_true)
print("MSE Loss:", mse.item())

# 交叉熵损失函数
ce_loss = nn.CrossEntropyLoss()
ce = ce_loss(y_pred.unsqueeze(0), y_true)
print("Cross-Entropy Loss:", ce.item())

# KL 散度损失函数
kl_loss = nn.KLDivLoss()
kl = kl_loss(y_pred.log().unsqueeze(0), y_true)
print("KL Divergence Loss:", kl.item())

# Hinge Loss损失函数
hinge_loss = nn.HingeEmbeddingLoss()
y_pred_binary = torch.tensor([1.2, -0.5, 0.8])  # 预测结果（二分类问题）
hinge = hinge_loss(y_pred_binary, y_true)
print("Hinge Loss:", hinge.item())