Verilog | 卷积码实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了Verilog | 卷积码实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、卷积码(convolution code)

卷积码是一种差错控制编码，由P.Elias于1955年发明。因为数据与二进制多项式滑动相关故称卷积码。卷积码在通信系统中应用广泛，如IS-95，TD-SCDMA，WCDMA，IEEE 802.11及卫星等系统中均使用了卷积码。以（n,k,m）或者（n,k,L）来描述卷积码，其中k为每次输入到卷积编码器的bit数，n为每个k元组码字对应的卷积码输出n元组码字，m为编码存储度，也就是卷积编码器的k元组的级数，称m+1= L为编码约束度m称为约束长度。卷积码将k元组输入码元编成n元组输出码元，但k和n通常很小，特别适合以串行形式进行传输，时延小。与分组码不同，卷积码编码生成的n元组元不仅与当前输入的k元组有关，还与前面m-1个输入的k元组有关，编码过程中互相关联的码元个数为n*m。卷积码的纠错性能随m的增加而增大，而差错率随N的增加而指数下降。在编码器复杂性相同的情况下，卷积码的性能优于分组码。

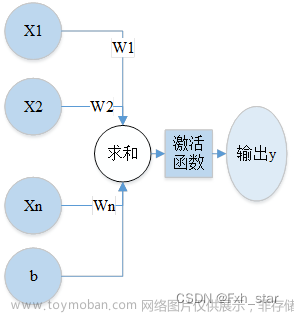
当输入信息比特数为 1 位，约束长度为 K 时，可以画出卷积编码器如图所示：

Verilog | 卷积码实现

卷积码可以用解析式表示法、图形表示法等方式来表示，而图形表示法又可分为状态图、树图、网络图等方式。

其中最重要的就是网络图。

Verilog | 卷积码实现

网络图横坐标表示时刻纵坐标表示状态，状态数与约束长度相关。实线表示输入 0 所走分支，虚线表示输入 1 所走分支，线上的数字表示输出的码字。任意给定一个信息序列，网络图中就存在一条特定的路径。这就是研究卷积码最大似然译码维特比算法的重要工具。

通常卷积码编码器开始工作前都要进行初始化，按编码器的初始状态的不同可以分为两类：

末尾补零卷积码(Tail-bits)：

通常卷积码编码器开始工作时都要进行初始化，编码开始前将编码器的所有寄存器单元都进行清零处理。而在编码结束时，需要添加0到码流末尾(Tailed Termination)，使编码器状态归零, 这即是末尾补零卷积码。相对于编码比特而言，添加的末尾比特增加了编码开销。

咬尾卷积码(Tail biting)：

咬尾卷积编码是一种特殊的卷积编码，它通过将编码器的移位寄存器的初始值设置为输入流的末尾比特值，使得移位寄存器的初始和最终状态相同。编码器开始工作时要进行特殊的初始化，将输入信息比特的最后m个比特依次输入编码器的寄存器中，当编码结束时，编码器的结束状态与初始状态相同。由于这个编码方法没有出现尾比特，因此称为咬尾编码。咬尾编码减少了尾比特的编码开销。对于咬尾编码方法，在译码过程中，由于编码器的初始状态和结尾状态是未知的，因此就需要增加一定的译码复杂度，才能确保好的译码性能。和普通的卷积编码相比，咬尾的方案最大的优点是克服了编码时的码率损失，并且适合迭代译码，不过付出的代价是译码复杂度的增加。

二、代码实现

//使用末尾补零卷积码的编码方式，代码还不够简洁，使用移位寄存器或许会更好一些，，，

/******************************************************/
	module viterbi_encode9(X,Y,Clock,Reset); 
/******************************************************/

input X, Clock, Reset;

output [1:0] Y; 

wire [1:0] Yt;
wire X, Clock, Reset;

wire [8:0] PolyA, PolyB;
wire [8:0] wA, wB, ShReg;

//   assign   PolyA = 9'b111_101_011;
//   assign   PolyB = 9'b101_110_001;

   assign   PolyA = 9'b110_101_111;
   assign   PolyB = 9'b100_011_101;

   assign wA = PolyA & ShReg;
   assign wB = PolyB & ShReg;

   assign ShReg[8] = X;
   pDFF dff7(ShReg[8], ShReg[7], Clock, Reset);
   pDFF dff6(ShReg[7], ShReg[6], Clock, Reset);   
   pDFF dff5(ShReg[6], ShReg[5], Clock, Reset);
   pDFF dff4(ShReg[5], ShReg[4], Clock, Reset);
   pDFF dff3(ShReg[4], ShReg[3], Clock, Reset);
   pDFF dff2(ShReg[3], ShReg[2], Clock, Reset);
   pDFF dff1(ShReg[2], ShReg[1], Clock, Reset);
   pDFF dff0(ShReg[1], ShReg[0], Clock, Reset);

   assign Yt[1] = wA[0] ^ wA[1] ^ wA[2] ^ wA[3] ^ wA[4] ^ wA[5] ^ wA[6] ^ wA[7] ^ wA[8];
   assign Yt[0] = wB[0] ^ wB[1] ^ wB[2] ^ wB[3] ^ wB[4] ^ wB[5] ^ wB[6] ^ wB[7] ^ wB[8];

   pDFF dffy1(Yt[1], Y[1], Clock, Reset);
   pDFF dffy0(Yt[0], Y[0], Clock, Reset);
endmodule

/******************************************************/
	module pDFF(DATA,QOUT,CLOCK,RESET);
/******************************************************/

parameter WIDTH = 1; 

input [WIDTH-1:0] DATA;
input CLOCK, RESET;

output [WIDTH-1:0] QOUT;

reg [WIDTH-1:0] QOUT;

   always @(posedge CLOCK or negedge RESET)
      if (~RESET) QOUT <= 0; //active low reset
         else QOUT <= DATA;

endmodule

参考:

维特比译码器(Viterbi Decoder)硬件架构(一)–卷积码及编解码算法介绍

Encoding/Decoding - Presentation of Convolutional Code文章来源地址https://www.toymoban.com/news/detail-497246.html

到了这里，关于Verilog | 卷积码实现的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！