概率论与数理统计_数理统计部分-Toy模板网

这篇具有很好参考价值的文章主要介绍了概率论与数理统计_数理统计部分。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数理统计方面的相关符号
符号	符号意义
X或F(x)	总体
𝒙𝟏,𝒙𝟐,...,𝒙𝒏	样本𝑿𝟏,𝑿𝟐,...,𝑿𝒏的观察值，简称样本值
𝒏	样本大小或样本容量
𝐹𝑛(𝑥)	经验分布函数
𝑌∼𝜒2(𝑛)	服从自由度为𝑛的𝜒2分布
𝑇∼𝑡(𝑛)	服从自由度为𝑛的𝑡分布
𝐹∼𝐹(𝑛1,𝑛2)	服从自由度为𝑛1和𝑛2的𝐹分布

相关概念与例题

背景

数理统计的主要任务：研究怎样以有效的方式收集、整理和分析带有随机性的数据，对所考察的问题作出推断和预测，为决策和行动提供依据和建议.

总体与样本

统计推断——从全体研究对象中抽取部分个体进行实验，利用概率论的理论对所得数据进行处理，从而获得对研究对象统计规律的推测，这种思想的实现称为统计推断。

参数估计和假设检验是统计推断的两个基本方法。

总体——在数理统计中，把研究对象的全体称为总体或母体。（试验全部可能的观察值）

有限总体: 包括有限个个体的总体。

无限总体: 包括无限个个体的总体。

我们要研究的总体实质上就是某个概率分布，因此我们将总体定义为一个概率分布或服从这个分布的随机变量。

个体——组成总体的每一个研究对象称为个体。（每一个可能的观察值）

抽样——为推断总体分布及各种特征，按一定规则从总体中抽取若干个体进行观察试验，以获得有关总体的信息，这一抽取过程称为“抽样”。

样本——被抽取的部分个体称为总体的一个样本。
样本容量——样本中所包含的个体数目称为样本容量。

样本是𝒏个随机变量𝑿𝟏,𝑿𝟐,...,𝑿𝒏，它们满足：（独立同分布）

1. 独立性：𝑿𝟏,𝑿𝟐,...,𝑿𝒏是相互独立的随机变量

2. 代表性：𝑿𝟏,𝑿𝟐,...,𝑿𝒏中每一个与所考察的总体有相同的分布

当取样完成后，我们就得到𝒏个具体的数据：𝒙𝟏,𝒙𝟐,...,𝒙𝒏，称之为样本𝑿𝟏,𝑿𝟐,...,𝑿𝒏的样本观察值，简称样本值，并称𝒏为样本大小或样本容量。

样本的联合分布律

实际操作中，怎样获得简单随机样本？

对于有限总体，采用放回抽样，就能得到简单随机样本。

当个体的总数𝑵比样本容量𝒏大得多时，实际中可将不放回抽样近似地当做放回抽样来处理

对于无限总体，总是用不放回抽样。

统计量

设𝑋1,𝑋2,⋯,𝑋𝑛为来自总体𝑋的一个样本，𝑔(𝑋1,𝑋2,⋯,𝑋𝑛)为一连续函数，若𝑔中不含有总体的任何未知参数，则称𝑇=𝑔(𝑋1,𝑋2,⋯,𝑋𝑛)为统计量。【考点】

𝑔(𝑋1,𝑋2,⋯,𝑋𝑛)为连续函数是为保证统计量𝑇是一随机变量。当样本𝑋1,𝑋2,⋯,𝑋𝑛取定观测值𝑥1,𝑥2,...,𝑥𝑛后，𝑇=𝑔(𝑋1,𝑋2,⋯,𝑋𝑛)为一常量或者观察值。

常用统计量【重点】

概率论与数理统计_数理统计部分

直方图

横坐标表示数据，纵坐标有三种表示方法：频数、频率、频率/组距。

频率直方图可以反映出连续型随机变量的频率分布情况

【绘制步骤】
1. 找出样本数据中的最小值和最大值，确定数据的取值区间；
2. 将区间等分为m个子区间，用横坐标来刻画；
3. 统计数据落在每个子区间上的频数，计算频率及各直方块的高度，用纵坐标来刻画。

经验分布函数

设𝑋1,𝑋2,⋯,𝑋𝑛是总体𝐹的一个样本，用𝑆(𝑥)表示𝑋1,𝑋2,⋯,𝑋𝑛中不大于𝑥的随机变量的个数，定义经验分布函数𝑭𝒏(𝒙)为：𝐹𝑛(𝑥)=1/𝑛 * 𝑆(𝑥)，−∞<𝑥<+∞

对于给定的样本值，经验分布函数的观察值很容易得到。经验分布𝐹𝑛(𝑥)的观察值仍以𝐹𝑛(𝑥)表示。

经验分布函数观察值的求法：
一般地，设𝑥1,𝑥2,⋯,𝑥𝑛是总体𝐹的一个容量为𝑛的样本值。将𝑥1,𝑥2,⋯,𝑥𝑛按从小到大的次序排列，并重新编号，设为𝑥1≤𝑥2≤⋯≤𝑥𝑛
则经验分布𝐹𝑛(𝑥)的观察值（分布函数，概率）为

格利文科(Glivenko)定理
对于任意实数𝑥, 经验分布函数𝐹𝑛(𝑥)以概率1一致收敛于总体分布函数𝐹(𝑥)即：
含义是：当𝑛充分大，“对于任意实数, 经验分布函数与总体分布函数之差的绝对值都很小”这个事件发生的概率等于1。
定理表明，当样本容量充分大，经验分布函数常常是对总体分布函数的很好近似。这一结论是数理统计依据样本来推断总体特征的理论基础。

正态总体的抽样分布

前言复习

概率论与数理统计_数理统计部分

𝝌𝟐分布

定义：设𝑋1,𝑋2,⋯,𝑋𝑛相互独立且均服从标准正态分布，则随机变量𝑌=𝑋1^2+𝑋2^2+⋯+𝑋𝑛^2服从自由度为𝑛的𝜒2分布，记为𝑌∼𝜒2(𝑛)。
密度函数（不重要，知晓图形趋势即可）
概率论与数理统计_数理统计部分

𝝌𝟐分布的性质：

（1）可加性：若𝑿~𝝌𝟐(𝒏)，𝒀~𝝌𝟐(𝒎)，且𝑿和𝒀相互独立，则𝑿+𝒀~𝝌𝟐(𝒏+𝒎)

（2）设𝑿𝟏,𝑿𝟐,⋯,𝑿𝒏相互独立，且均服从正态分布𝑿𝒊∼𝑵(𝝁,𝝈^𝟐)，则

（3）数学期望与方差：若𝑿~𝝌𝟐(𝒏)，则𝑬(𝑿)=𝒏,𝑫(𝑿)=𝟐𝒏。证明如下：

例题设总体𝑋~𝑁(0,1),𝑋1,𝑋2,⋯,𝑋6为取自总体𝑋的样本,令𝑌=(𝑋1+𝑋2+𝑋3)^2+(𝑋4+𝑋5+𝑋6)^2，求常数𝐶和n使得𝐶𝑌~𝜒2(n)。

解：

【注意】𝜎与𝜎^2，以及相加的关系

𝒕分布

定义：设𝑋~𝑁(0,1),𝑌∼𝜒2(𝑛)且𝑋和𝑌相互独立，则随机变量概率论与数理统计_数理统计部分服从自由度为𝑛的𝑡分布，记为𝑇∼𝑡(𝑛)。
密度函数（不重要，知晓图形趋势即可）

𝒕分布的性质：

1.𝑡分布的密度函数𝑓(𝑥)关于𝑥=0对称。当𝑛充分大时，由T函数的性质有：，即𝑛充分大时𝑡(𝑛)分布近似于𝑁(0,1)分布，但对于较小的𝑛，𝑡(𝑛)分布与𝑁(0,1)分布相差很大。

2. 具有自由度为𝑛的𝑇∼𝑡(𝑛)分布，其期望与方差为𝐸(𝑇)=0,𝑛>1，𝐷(𝑇)=𝑛/(𝑛−2),𝑛>2

例题设𝑋1,𝑋2,⋯,𝑋5为取自总体𝑋的样本,相互独立且均服从标准正态分布，若服从𝑡(𝑛)分布，则𝑑和𝑛的取值？

解：

【注意】记得t分布的公式的条件，分母上需要服从标准正态分布

𝑭分布

定义：设𝑋∼𝜒2(𝑛1)，𝑌∼𝜒2(𝑛2)，且𝑋和𝑌相互独立,则随机变量概率论与数理统计_数理统计部分，服从自由度为𝑛1和𝑛2的𝐹分布，记为𝐹∼𝐹(𝑛1,𝑛2)
密度函数（不重要，知晓图形趋势即可）

例题已知𝑋∼𝑡(𝑛)，证明𝑋^2∼𝐹(1,𝑛)。

证明：因𝑋∼𝑡(𝑛)，则存在𝑈∼𝑁(0,1),𝑉∼𝜒^2(𝑛)，且𝑈和𝑉相互独立，使得，即t分布的公式

于是，。

【注意】这里的不是𝝌𝟐分布，注意相关式子的左右侧

上侧分位点

设随机变量𝑋的分布为已知

在概率论中，常常需要计算对于给定𝑥的概率𝑃{𝑋≤𝑥}=𝑝，

而在数理统计中，常常需要对给定的𝑝(0<𝑝<1)，求出使𝑃{𝑋>𝑥}=𝑝的𝑥。

定义：给定𝛼(0<𝛼<1)，若数λ𝛼使得𝑃{𝑋>λ𝛼}=𝛼即𝐹(λ𝛼)=1−𝛼则称λ𝛼为此概率分布的𝛼上侧分位点或临界值。（λ𝛼为随机变量取的数，𝛼为概率）

标准正态分布的上侧分位点

1）定义：设𝑋~𝑁(0,1)，对于给定的𝛼(0<𝛼<1)，使𝑃{𝑋>𝑧(𝛼)}=𝛼或成立的𝑧(𝛼)称为标准正态分布𝛼的上侧分位点。

2）Φ(𝑧(𝛼))=𝑃{𝑋≤𝑧(𝛼)}==1−𝛼

3）−𝑧(𝛼)=𝑧(1−𝛼)

𝝌𝟐分布的上侧分位点

定义：设𝑋~𝜒2(𝑛)，对于给定的𝛼(0<𝛼<1)，使𝑃{𝑋>(𝜒𝛼)^2(𝑛)}=𝛼或成立的(𝜒𝛼)^2(𝑛)称为𝜒2分布𝛼的上侧分位点。

当自由度大于45时，可用近似公式：

t分布的上侧分位点

定义：设𝑋~𝑡(𝑛)，对于给定的𝛼(0<𝛼<1)，使𝑃{𝑋>𝑡𝛼(𝑛)}=𝛼或成立的𝑡𝛼(𝑛)称为𝑡(𝑛)分布𝛼的上侧分位点。

对称性：−𝑡( 𝛼(𝑛) )=𝑡( 1−𝛼(𝑛) )

由𝑡分布的性质：当𝑛趋于无穷时，𝑡分布的极限分布是正态分布，所以当自由度大于45时，可用标准正态分布来近似：𝑡𝛼(𝑛)≈𝑧𝛼

𝑭分布的上侧分位点

定义：设𝑋~𝐹(𝑛1,𝑛2)，对于给定的𝛼(0<𝛼<1)，使𝑃{𝑋>𝐹𝛼(𝑛1,𝑛2)}=𝛼或成立的𝐹𝛼(𝑛1,𝑛2)称为𝐹(𝑛1,𝑛2)分布𝛼的上侧分位点。

定理：

抽样分布定理【重点】

定理1：设总体𝑋~𝑁(𝜇,𝜎^2)，𝑋1,𝑋2,⋯,𝑋𝑛是𝑋的一个样本，则概率论与数理统计_数理统计部分或，其中为样本均值。

定理2：设总体𝑋~𝑁(𝜇,𝜎^2)，𝑋1,𝑋2,⋯,𝑋𝑛是𝑋的一个样本，则概率论与数理统计_数理统计部分

定理3：设总体𝑋~𝑁(𝜇,𝜎^2)，𝑋1,𝑋2,⋯,𝑋𝑛是𝑋的一个样本，则概率论与数理统计_数理统计部分。

点估计

前言

研究统计量的性质和评价一个统计推断的优良性，完全取决于其抽样分布的性质。
统计推断：对总体的未知参数进行估计；对关于参数的假设进行检验。
概率论与数理统计_数理统计部分

点估计【重点】

设总体𝑋的分布函数𝐹(𝑥,𝜃)形式已知，但其包含未知参数𝜃（可以是一个或者多个参数）。借助于总体𝑋的一个样本来估计总体的未知参数的值，称为点估计问题。
点估计问题就是要构建一个适当的统计量^𝜃(𝑋1,𝑋2,⋯,𝑋𝑛)，用它的观察值^𝜃(𝑥1,𝑥2,⋯,𝑥𝑛)来估计未知参数𝜃。
对于正态分布，样本均值概率论与数理统计_数理统计部分是𝜇的无偏估计，𝑆^2是𝜎^2的无偏估计

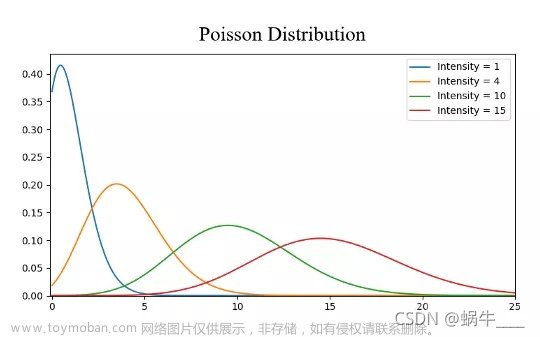
例题在某炸药制造厂，一天中发生着火现象的次数𝑋是一个随机变量，假设它服从以𝜆>0为参数的泊松分布，参数𝜆为未知，设有以下样本值，试估计参数λ。

解：因为𝑋~P(𝜆),所以𝜆=𝐸(𝑋)。用样本均值来估计总体的均值𝐸(𝑋)，即
=1/250 *(0×75+1×90+2×54+3×22+4×6+5×2+6×1)=1.22，
故估计参数𝜆的值为1.22

矩估计方法【重点】

矩估计法——用样本原点矩估计相应的总体原点矩，又用样本原点矩的连续函数估计相应的总体原点矩的连续函数，这种参数点估计法称为矩估计法。

矩估计的基本步骤：
设总体𝑋的分布函数中含有𝑘个未知参数𝜃1,𝜃2⋯,𝜃𝑘
1.总体𝑋的𝑘阶矩α1,α2,...,α𝑘,一般地都是总体分布中的参数𝜃1,𝜃2⋯,𝜃𝑘的函数，记为𝜇𝑖=𝜇𝑖(𝜃1,𝜃2⋯,𝜃𝑘)，𝑖=1,2,⋯,𝑘
2.从这𝑘个方程中解出：𝜃𝑗=𝜃𝑗(𝜇1,𝜇2,...,𝜇𝑘)，𝑗=1,2,⋯,𝑘
3.用诸𝜇𝑖的估计量A𝑖分别代替上式的诸𝜇𝑖，即可得诸𝜃𝑗的矩估计量^𝜃𝑗=𝜃𝑗(𝐴1,𝐴2,⋯,𝐴𝑘),𝑗=1,2,⋯,𝑘
矩估计量的观察值称为矩估计值。
【注意】A𝑖是𝜇𝑖的估计值，即𝜇𝑖是样本𝑘阶原点矩的观测值，A𝑖是样本𝑘阶原点矩，简便方法是：𝜇𝑖=E(X^i)

例题设总体𝑋在[𝑎,𝑏]上服从均匀分布，其中𝑎,𝑏均未知，𝑋1,𝑋2,⋯,𝑋𝑛是来自总体的样本，求𝑎,𝑏的估计量。

解：

【注意】用诸𝜇𝑖的估计量A𝑖分别代替上式的诸𝜇𝑖后，还需要用样本𝑋1,𝑋2,⋯,𝑋𝑛及其相关内容进行化简。

例题设总体𝑋的均值𝜇和方差𝜎^2都存在，且有𝜎>0，但𝜇和𝜎^2均为未知，又设𝑋1,𝑋2,⋯,𝑋𝑛是一个样本，求𝜇和𝜎^2的矩估计量。

解：𝜇1=𝐸(𝑋)=𝜇,𝜇2=𝐸(𝑋^2)=𝐷(𝑋)+𝐸(𝑋)^2=𝜎^2+𝜇^2,令𝜇=𝐴1,𝜎^2+𝜇^2=𝐴2.

解方程组得到矩估计量分别为。

极大似然估计方法【重点】

适用范围：总体分布类型已知时。
极大似然法的基本思想：参数（p）的选择应对所出现的观察结果最有利，即参数（p）的选择应使观察结果出现的概率最大。
极大似然估计——设𝑥1,𝑥2,⋯,𝑥𝑛是取自总体𝐹(𝑥;𝜃)的样本观察值，如果当未知参数𝜃取^𝜃时，(𝑥1,𝑥2,⋯,𝑥𝑛)被取到的概率最大，则称^𝜃为𝜃的极大似然估计。

其求法如下：
1）构建似然函数𝐿(𝜃)=𝐿(𝑥1,𝑥2,⋯,𝑥𝑛;𝜃)
若总体是离散型分布，其分布律为𝑃{𝑋=𝑥}=𝑝(𝑥;𝜃)其中𝜃为未知参数，则样本的联合分布律为

若总体为连续型，其概率密度为𝑓(𝑥;𝜃)，则样本的联合概率密度为

2）求似然函数𝐿(𝜃)=𝐿(𝑥)1,𝑥2,⋯,𝑥𝑛;𝜃的最大值点^𝜃

若似然函数𝐿是𝜃的可微函数，则最大值点^𝜃必满足似然方程𝑑𝐿/𝑑𝜃=0
从中解得𝜃，经过检验即可得到𝐿的最大值点^𝜃，^𝜃就是𝜃的极大似然估计。由于𝐿为乘积函数，而𝐿与ln𝐿在同一处取得最大值，所以由对数似然方程 𝑑ln𝐿/𝑑𝜃=0 求解^𝜃。

例题设𝑋1,𝑋2,⋯,𝑋𝑛是取自总体𝑋~𝐵(1,𝑝)的一个样本，求参数𝑝的极大似然估计。

例题已知总体𝑋~𝑁(𝜇,𝜎^2)，𝜇和𝜎^2均未知，求这两个参数的极大似然估计。

区间估计

基本概念

参数的区间估计——由样本给出未知参数的一个估计范围(称为估计区间)，并使其包含未知参数真值的可靠性达到一定的要求，是对未知参数的另一种估计方法，这就是参数的区间估计。

设𝑋1,𝑋2,...,𝑋𝑛是来自总体𝑋的样本，𝑋的分布𝐹(𝑥;𝜃)中含有未知参数𝜃。
对给定的数𝛼(0<𝛼<1)，若有统计量^𝜃1=^𝜃1(𝑋1,𝑋2,...,𝑋𝑛)和^𝜃2=^𝜃2(𝑋1,𝑋2,...,𝑋𝑛)(^𝜃1<^𝜃2)使得𝑃{^𝜃1<𝜃<^𝜃2}=1−𝛼，则称随机区间(^𝜃1,^𝜃2)是𝜃的一个双侧置信区间，称1−𝛼为置信度(置信水平)（可靠度），称^𝜃1和^𝜃2是该双侧置信区间的置信下限和置信上限。
【注意】区分上侧分位点𝛼与置信度1−𝛼
确切的解释是：随机区间(^𝜃1,^𝜃2)包含𝜃的概率是1−𝛼。

置信度𝟏−𝜶是指：参数𝜃的真值在置信区间内的可靠程度(可信度)。
置信区间的长度则是对估计精度的度量。置信区间的长度越短，表示估计的精度越高。即：在概率密度为单峰且对称的情形，当𝒂=−𝒃时求得的置信区间的长度为最短。即使在概率密度不对称的情形，如𝝌𝟐分布，F分布，习惯上仍取对称的分位点来计算未知参数的置信区间。
在求置信区间时，要查表求分位点。

求未知参数𝜽的置信区间的步骤如下:
1.寻找一个样本𝑋1,𝑋2,...,𝑋𝑛的函数：𝐺=𝑔(𝑋1,𝑋2,...,𝑋𝑛;𝜃)，它包含待估参数𝜃，但不包含其它未知参数，并且𝐺的分布已知且不依赖于任何未知参数。
2.对于给定的置信水平1−𝛼，定出两个常数𝑎和𝑏，使得𝑃{𝑎<𝑔(𝑋1,𝑋2,...,𝑋𝑛;𝜃)<𝑏}=1−𝛼
3.若能从𝑎<𝑔(𝑋1,𝑋2,⋯,𝑋𝑛;𝜃)<𝑏得到等价的不等式^𝜃1<𝜃<^𝜃2，其中^𝜃1=^𝜃1(𝑋1,𝑋2,⋯,𝑋𝑛)，^𝜃2=^𝜃2(𝑋1,𝑋2,⋯,𝑋𝑛)都是统计量，那么(^𝜃1,^𝜃2)就是𝜃的一个置信度为1−𝛼的置信区间。

例题设总体𝑋~𝑁(𝜇,𝜎^2)，𝜎^2为已知，𝜇为未知, 设𝑋1,𝑋2,...,𝑋𝑛是来自𝑋的样本,求𝜇的置信度为0.95的置信区间。

【注意】给定样本，给定置信水平，置信区间也不是唯一的。对同一个参数，我们可以构造许多置信区间。

在概率密度为单峰且对称的情形，当𝒂=−𝒃时求得的置信区间的长度为最短。即使在概率密度不对称的情形，如𝝌𝟐分布，F分布，习惯上仍取对称的分位点来计算未知参数的置信区间。

单正态总体参数的区间估计

1. 𝜎^2已知时，求𝝁的置信区间

由上述例题可知，𝜇的置信水平为1−𝛼的一个置信区间为概率论与数理统计_数理统计部分

2. 𝜎^2未知时，求𝝁的置信区间

因为𝑆^2是𝜎^2的无偏估计，可用𝑆替换𝜎，由第六章学过的定理3可知概率论与数理统计_数理统计部分

概率论与数理统计_数理统计部分

例题有一大批糖果，现从中随机地取16袋，称得重量(克)如下：

506 508 499 503 504 510 497 512 514 505 493 496 506 502 509 496

设袋装糖果的重量服从正态分布，试求总体均值的置信度为0.95的置信区间。

3. 求𝜎^2的置信区间

因𝑆^2是𝜎^2的无偏估计，可以以𝑆^2为基础来构建𝜎^2的置信区间。根据第六章学习的定理2可知：概率论与数理统计_数理统计部分

对于给定的𝛼，查附表得𝜒2分布得分位点，使得
概率论与数理统计_数理统计部分

例题有一大批糖果，现从中随机地取16袋，称得重量(克)如下：

506 508 499 503 504 510 497 512 514 505 493 496 506 502 509 496

设袋装糖果的重量服从正态分布，试求总体方差的置信度为0.95的置信区间。

假设检验的基本概率

假设检验问题的提法、原则与基本步骤

假设检验问题——根据样本的信息检验关于总体的某个假设是否正确，这类问题称作假设检验问题。

假设检验问题主要包括：
（1）已知总体分布的形式，需对其中的未知参数给出假设检验—参数检验
（2）总体的分布形式完全未知的情况下，对总体的分布或数字特征进行假设检验—非参数检验

通常的办法是进行抽样检查。

假设检验的基本思想：
（1）提出假设：𝑯𝟎为原假设（或零假设）; 𝑯𝟏为备选假设（或对立假设）
（2）选检验统计量，已知总体分布时根据总体分布的式子进行选定
（3）对给定的显著性水平𝛼，可以在𝑁(0,1)表中查到分位点的值𝑧(𝛼/2)，使𝑃{|Z|>𝑧(𝛼/2)}=𝛼，确定H0的拒绝域W
（4）由样本观察值计算统计量观察值t
（5）作出判断：当t∈W时，则拒绝H0，否则不拒绝H0，即认为在显著水平𝛼下，H0与实际情况差异不显著

如果𝐻0是对的，那么衡量差异大小的某个统计量落入拒绝域𝑊（𝑊:|Z|>𝑧(𝛼/2)）是个小概率事件。如果该统计量的实测值落入了𝑊，说明𝐻0成立下的小概率事件发生了，那么就认为𝐻0不可信而否定它。否则我们就不能否定𝐻0。
而不否定𝐻0并不是肯定𝐻0一定对，而只是说差异还不够显著，还没有达到足以否定𝐻0的程度。所以假设检验又叫“显著性检验”。

如果显著性水平𝛼取得很小，则拒绝域𝑊也会比较小。产生的后果是：𝐻0难于被拒绝。
如果在𝛼很小的情况下𝐻0仍被拒绝了，则说明实际情况很可能与之有显著差异。
基于这个理由，人们常把𝜶=0.05 时拒绝𝐻0称为是显著的，而把在𝜶=0.01 时拒绝𝐻0称为是高度显著的。

【注意】注意区分上侧分论点𝛼、置信水平1-𝛼和显著水平𝛼

例题某工厂生产的一种螺钉，标准要求长度是32.5毫米。实际生产的产品，其长度𝑋假定服从正态分布𝑁(𝜇,𝜎^2)，𝜎^2未知，现从该厂生产的一批产品中抽取6件，得尺寸数据如下：32.56, 29.66, 31.64, 30.00, 31.87, 31.03，此时显著水平𝜶=0.01，问这批产品是否合格?

分析：这批产品（螺钉长度）的全体组成问题的总体𝑋。现在要检验𝐸(𝑋)是否为32.5。此时相当于𝜎^2未知，关于𝝁的检验。

解：第一步：提出原假设和对立假设
𝐻0:𝜇=32.5 𝐻1:𝜇≠32.5
第二步：取一检验统计量（能衡量差异大小且分布已知），在𝑯𝟎成立下求出它的分布

第三步：对给定的显著水平𝜶=0.01 ，查表确定临界值：

𝑡𝛼/2(5)=𝑡0.005(5)=4.0322使得𝑃{|𝑇|>𝑡𝛼/2(5)}=𝛼，即“|𝑇|>𝑡𝛼/2(5)”是一小概率事件，并得到拒绝域𝑊:|𝑇|>4.0322

第四步：将样本值代入算出统计量𝑇的实测值𝑇=2.997<4.0322故不能拒绝𝐻0

注意：这并不意味着𝑯𝟎一定对，只是差异还不够显著，不足以否定𝑯𝟎

两种错误

【注意】需要区分第一类错误和第二类错误，并记住其代表的内容概率论与数理统计_数理统计部分

第一类错误：当H0为真时，却拒绝了H0，也称这类错误为去真错误。
第二类错误：当H0不真时，却接受了H0，也称这类错误为存伪错误。

关于正态总体的假设检验

1. 𝝈^𝟐已知，关于𝝁的检验

可以提出三种假设检验问题：
（i）𝐻0:𝜇=𝜇0⇔𝐻1:𝜇≠𝜇0（通常）
（ii）𝐻0:𝜇≤𝜇0⇔𝐻1:𝜇>𝜇0
（iii）𝐻0:𝜇≥𝜇0⇔𝐻1:𝜇<𝜇0
当对立假设𝐻1分散在原假设𝐻0两侧时的检验称为双侧检验，否则称为单侧检验。

由于𝜎已知，选检验统计量概率论与数理统计_数理统计部分，
对于假设检验问题𝐻0:𝜇=𝜇0，对给定的显著性水平𝛼，其拒绝域为：

对于假设检验问题𝐻0:𝜇≤𝜇0，构造的拒绝域为：概率论与数理统计_数理统计部分

对于假设检验问题𝐻0:𝜇≥𝜇0，构造的拒绝域为：概率论与数理统计_数理统计部分

2. 𝝈^𝟐未知，关于𝝁的检验

对于上述的假设检验，我们选用的检验统计量为：概率论与数理统计_数理统计部分

例题某种元件的寿命𝑋（以小时记）服从正态分布𝑁(𝜇,𝜎^2)，𝜇,𝜎^2均未知。现测得16只元件的寿命如下：159 280 101 212 224 379 179 264222 362 168 250 149 260 485 170

问是否有理由认为元件的平均寿命大于225（小时）？（取显著性水平为0.05）

解：按题意需检验𝐻0:𝜇≤𝜇0=225，𝐻1:𝜇>225.

拒绝域为：

没有落在拒绝域内，故不能拒绝原假设，认为元件的平均寿命不大于225小时。

3.均值𝝁未知时，关于方差𝝈^𝟐的检验

对于上述的假设检验，我们选用的检验统计量为：概率论与数理统计_数理统计部分

例题某炼铁厂铁水中碳含量的百分数𝑋服从正态分布𝑁(𝜇,0.112^2)，现在对工艺进行改进，从中选取7炉铁水，测得碳含量的百分数为4.411，4.062，4.337，4.394，4.346，4.277，4.693，试问新工艺炼出铁水碳含量百分数的方差是否有显著性改变（𝛼=0.05）？

解：这里的零假设为𝐻0:𝜎^2=0.112^2⇔𝐻1:𝜎^2≠0.112^2

根据均值未知时，方差假设检验的（i），拒绝域为

因𝜒2落在拒绝域内，故拒绝原假设，认为新工艺炼出铁水碳含量百分数的方差有显著性改变。