👻内容专栏:《C/C++专栏》
🐨本文概括: 计算高精度的2的N次方数字。
🐼本文作者:花 碟
🐸发布时间:2023.6.22
前言
为什么不直接利用int、float、double等类型进行存储计算,因为它们是存在有效数据范围的, 比如说int的范围是 -2147483648 ~ 2147483647 字节,数值最多占据10位,8字节的 long int 型的取值范围是-9,223,372,036,854,775,808~9,223,372,036,854,775,807,而如果想存储更大的数字的话,有效范围之内并不能容忍得下,超出的数据就会导致精度的丢失,故而以下解法是针对高精度计算问题,利用数组的每一个元素去模拟数值的位数。😉👇
求2的N次方,N ≤ 10000
首先,我们应该要把数字存储倒序存储到数组当中,数值的
个位放到数组a[0]的位置,十位放到数组a[1]的位置,百位放到数组a[2]的位置……依次类推,为什么要倒序存储呢,因为我们需要对数值进行运算,比如说如果将12345678912345正序存储,将这个数值乘上2,那么可能会涉及到进位运算,如果进位到最高位之后还需要进1,那么此时数组a[0]的位置就不容易修改了,所以我们将最低位放到数组首元素位置。

💡
实现思路:
⚠️注:为了方便理解,我们暂时将画图中给定的数值为 12345678912345。本题的实现,注意数组初始化必须为1,才能保证求2的N次幂得到想要的结果。
首先将2N转换为一共有多少位,取以10为底的对数,即 log102N,转换为N * log102 ,题目要求N最多取10000,换算大概3010多位,因为肯定含有进位,所以我们将数组的大小定义为3100个,从数组的a[0]位置模拟个位,a[1]位置模拟十位……开始计算,我们需要将数组的元素初始化为1,因为1乘以任何数都是任何数。然后用t来存储当前数值是否需要进行进位,如果是进位的话需要加到下个数值里面去,所以我们写成
t += a[j] * 2;然后将取模运算得下的个位数,放到b数组对应的位置(实现时,我们不需要开辟b数组,直接对a数组进行覆盖即可,这里方便理解,所以放到b数组之中),再继续运算,上一位进位的t加上本次a数组对应的值乘上2 依然能够整除10,那么结果为1,就表示进位,再给到t,否则为0,表示不进位。……以此类推,最后为了保证数组的有效个数的位置,我们用m来记录,一旦每次乘以2之后,t进位为1,就让m++。最后输出数组中的值,我们就要倒过来输出,我们从m - 1的位置一直输出的0即可,因为m++是后置的,多加了一次,所以m需要减去1。

代码实现:
😉😉文章来源:https://www.toymoban.com/news/detail-497662.html
#include <iostream>
const int N = 3300;
using namespace std;
int main() {
// 最低为数字是1,因为它乘以任何数都是任何数
int a[N] = {1};
int n;
cin >> n;
//m标记进位完后的位置
int m = 1;
// 输入的 n 是 2 的幂次,并非乘数
for (int i = 0; i < n; i++) {
int t = 0;
// 循环内的数字从低位不断被取出,这些数字都从左到右存放,也就是个位数在最左端,每次从数组a中读取个位十位,分别与 2 相乘
// 运算后把数字存回原数组
for (int j = 0; j < m; j++) {
t += a[j] * 2;
a[j] = t % 10;
t /= 10;
}
// 负责进位,for循环最后一个操作是 t / 10,由于乘以2,最大为19, 因此若商为1,必定进位1
if (t) a[m++] = 1;
}
//m多加了1次,减去1
for (int i = m - 1; i >= 0; i--) cout << a[i];
return 0;
}
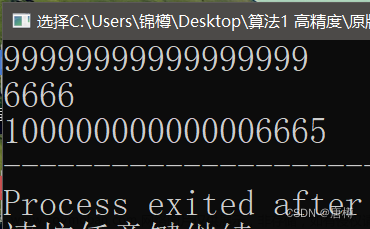
测试结果
输入10000,210000的结果如下: 文章来源地址https://www.toymoban.com/news/detail-497662.html
文章来源地址https://www.toymoban.com/news/detail-497662.html
到了这里,关于求2的N次幂(C++)解决高精度运算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!