综合评价方法
提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加
例如:第一章 Python 机器学习入门之pandas的使用
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
前言
评价方法大体上可分为两类,其主要区别在确定权重的方法上。一类是主观赋权法,多数采取综合咨询评分确定权重,如综合指数法、模糊综合评判法、层次分析法、功效系数法等。另一类是客观赋权,根据各指标间相关关系或各指标值变异程度来确定权数,如主成分分析法、因子分析法、理想解法(也称TOPSIS法)等。
一、理想解法
例14.1 研究生院试评估。
为了客观地评价我国研究生教育的实际状况和各研究生院的教学质量,国务院学位委员会办公室组织过一次研究生院的评估。为了取得经验,先选5所研究生院,收集有关数据资料进行了试评估,表14.1是所给出的部分数据。
clc, clear
a=[0.1 5 5000 4.7
0.2 6 6000 5.6
0.4 7 7000 6.7
0.9 10 10000 2.3
1.2 2 400 1.8];
[m,n]=size(a);
x2=@(qujian,lb,ub,x)(1-(qujian(1)-x)./(qujian(1)-lb)).*...
(x>=lb & x<qujian(1))+(x>=qujian(1) & x<=qujian(2))+...
(1-(x-qujian(2))./(ub-qujian(2))).*(x>qujian(2) & x<=ub);
qujian=[5,6]; lb=2; ub=12;
a(:,2)=x2(qujian,lb,ub,a(:,2)); %对属性2进行变换
b=a./vecnorm(a) %利用矩阵广播进行向量规范化
w=[0.2 0.3 0.4 0.1];
c=b.*w; %利用矩阵广播求加权矩阵
Cstar=max(c); %求正理想解
Cstar(4)=min(c(:,4)) %属性4为成本型的
C0=min(c); %q求负理想解
C0(4)=max(c(:,4)) %属性4为成本型的
Sstar=vecnorm(c-Cstar,2,2) %逐行计算2范数即到正理想解的距离
S0=vecnorm(c-C0,2,2) %逐行计算2范数即到负理想解的距离
f=S0./(Sstar+S0)
[sf,ind]=sort(f,'descend') %求排序结果
二、模糊综合评判法
例14.3 某部门员工的年终评定。
关于考核的具体操作过程,以对一名员工的考核为例。如表14.7所示,根据该部门工作人员的工作性质,将18个指标分成工作绩效( )、工作态度( )、工作能力( )和学习特长( )这4个子因素集。
三、数据包络分析
例14.4(多指标评价问题)某市教委需要对六所重点中学进行评价,其相应的指标如表14.8所示。表14.8中的生均投入和非低收入家庭百分比是输入指标,生均写作得分和生均科技得分是输出指标。请根据这些指标,评价哪些学校是相对有效的。
DEA最突出的优点是无须任何权重假设,每一输入输出的权重不是根据评价者的主观认定,而是由决策单元的实际数据求得的最优权重。因此,DEA方法排除了很多主观因素,具有很强的客观性。
利用DEA方法对天津市的可持续发展进行评价。在这里选取较具代表性的指标,作为输入变量和输出变量,见表14.9
输入变量:政府财政收入占GDP的比重、环保投资占GDP的比重、每千人科技人员数;输出变量:经济发展(用人均GDP表示)、环境发展(用城市环境质量指数表示)。
四、灰色关联分析

例14.6 供应商选择决策。
某核心企业需要在6个待选的零部件供应商中选择一个合作伙伴,各待选供应商有关数据见表14.11。
clc, clear
a=[0.83 0.90 0.99 0.92 0.87 0.95
326 295 340 287 310 303
21 38 25 19 27 10
3.2 2.4 2.2 2.0 0.9 1.7
0.20 0.25 0.12 0.33 0.20 0.09
0.15 0.20 0.14 0.09 0.15 0.17
250 180 300 200 150 175
0.23 0.15 0.27 0.30 0.18 0.26
0.87 0.95 0.99 0.89 0.82 0.94];
for i=[1 5:9] %效益型指标标准化
a(i,:)=(a(i,:)-min(a(i,:)))/(max(a(i,:))-min(a(i,:)));
end
for i=2:4 %成本型指标标准化
a(i,:)=(max(a(i,:))-a(i,:))/(max(a(i,:))-min(a(i,:)));
end
[m,n]=size(a);
ck=max(a,[],2); %逐行求最大值,得参考数列
t=ck-a; %求参考数列与每一个比较数列的差
mmin=min(min(t)); %计算最小差
mmax=max(max(t)); %计算最大差
rho=0.5; %分辨系数
xishu=(mmin+rho*mmax)./(t+rho*mmax) %计算灰色关联系数
guanliandu=mean(xishu) %取等权重,计算关联度
[gsort,ind]=sort(guanliandu,'descend') %对关联度按照从大到小排序
将灰色关联分析用于供应商选择决策中可以针对大量不确定性因素及其相互关系,将定量和定性方法有机结合起来,使原本复杂的决策问题变得更加清晰简单,而且计算方便,并可在一定程度上排除决策者的主观任意性,得出的结论也比较客观,有一定的参考价值。
五、主成分分析法

六、秩和比综合评价法
秩和比(Rank Sum Ration,RSR) 统计方法是我国统计学家田凤调教授于1988年提出的一种新的综合评价方法,该法在医疗卫生领域的多指标综合评价、统计预测预报、统计质量控制等方面已得到广泛的应用。秩和比是行(或列)秩次的平均值,是一个非参数统计量,具有0~1连续变量的特征。
某市人民医院1983~1992年工作质量统计指标及权重系数见表14.18,其中 为治愈率, 为病死率, 为周转率, 为平均病床工作日, 为病床使用率, 为平均住院日,这里 和 为成本型指标,其余为效益型指标。
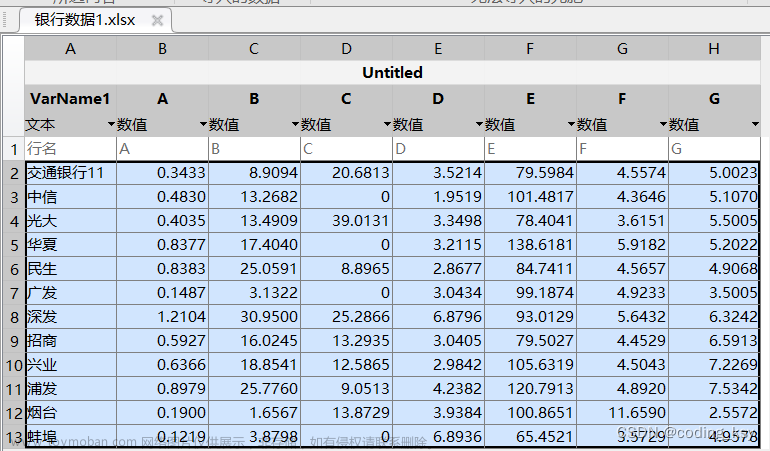
七、基于熵权法的评价方法


clc, clear
a=readmatrix('data14_9_1.txt');
[n,m]=size(a);
p=a./sum(a);
e=-sum(p.*log(p))/log(n);
g=1-e; w=g/sum(g) %计算权重
s=w*p' %计算各个评价对象的综合评价值
[ss,ind1]=sort(s,'descend') %对评价值从大到小排序
ind2(ind1)=1:n %学生编号对应的排序位置
writematrix(w,'data14_9_2.xlsx') %把数据写到Excel文件的表单1
writematrix([1:n;s;ind2],'data14_9_2.xlsx','Sheet',2) %把数据写到表单2
PagRank算法
 文章来源:https://www.toymoban.com/news/detail-498049.html
文章来源:https://www.toymoban.com/news/detail-498049.html
招聘公务员问题
clc, clear, close all
fx1=@(c)[(1+c(1)*(1-c(2))^(-2))^(-1)-0.01
(1+c(1)*(3-c(2))^(-2))^(-1)-0.8];
cs1=fsolve(fx1,rand(1,2)) %待定参数alpha,beta
fx2=@(c)[c(1)*log(3)+c(2)-0.8; c(1)*log(5)+c(2)-1];
cs2=fsolve(fx2,rand(1,2)) %待定参数a,b
fx=@(x)(1+cs1(1)*(x-cs1(2)).^(-2)).^(-1).*(x>=1 & x<=3)+...
(cs2(1)*log(x)+cs2(2)).*(x>3 & x<=5);
fplot(fx,[1,5]), f2=fx(2), f4=fx(4)
d0=load('anli14_1_1.txt'); d1=d0(:,[4:7]);
c=fx(d1); b=mean(c,2) %计算复试分数
writematrix(b','anli14_1_2.xlsx')
ma1=max(d0(:,1)), ma2=min(d0(:,1))
az=(d0(:,1)-ma2)/(ma1-ma2) %初试分标准化
mb1=max(b), mb2=min(b)
bz=(b-mb2)/(mb1-mb2) %复试分标准化
d=0.5*(az+bz) %计算综合得分
[sd, ind1]=sort(d, 'descend') %按照从大到小排序
ind2(ind1)=1:16
writematrix([d';ind2], 'anli14_1_2.xlsx', 'Sheet',1, 'Range', 'A3')
还有很多,关键讨论怎么确定对公务员的评价文章来源地址https://www.toymoban.com/news/detail-498049.html
到了这里,关于数学建模--综合评价方法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!