HELLO算法笔记之散列表（哈希）-Toy模板网

这篇具有很好参考价值的文章主要介绍了HELLO算法笔记之散列表（哈希）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、哈希表

建立键 key 与值 value 之间的映射，实现高效的元素查询。输入一个key，以O（1）获取对应的value

遍历：

# 遍历哈希表
# 遍历键值对 key->value
for key, value in mapp.items():
    print(key, "->", value)
# 单独遍历键 key
for key in mapp.keys():
    print(key)
# 单独遍历值 value
for value in mapp.values():
    print(value)

知识点1、哈希函数：

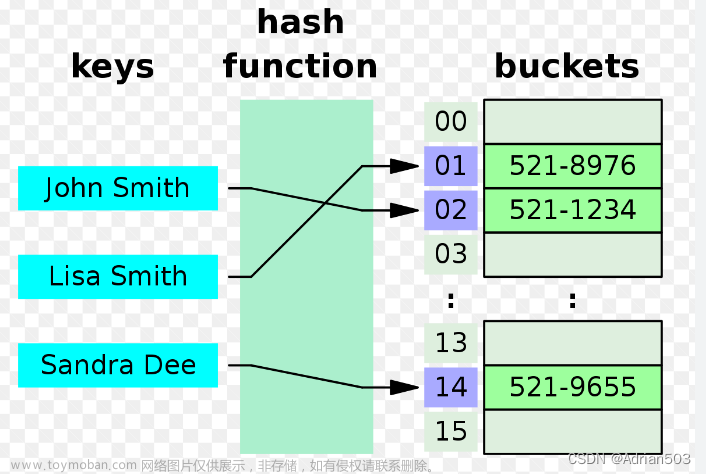
将一个较大的输入空间映射到一个较小的输出空间。在哈希表中，输入空间是所有 key ，输出空间是所有桶（数组索引）。换句话说，输入一个 key ，我们可以通过哈希函数得到该 key 对应的键值对在数组中的存储位置。

输入一个 key ，哈希函数的计算过程分为两步：首先，通过哈希算法 hash() 计算得到哈希值；接下来，将哈希值对桶数量（数组长度）capacity 取模，从而获取该 key 对应的数组索引 index 。

index = hash(key) % capacity

HELLO算法笔记之散列表（哈希）

每个桶都放着一个键值对

buckets[index] =Pair(key, val)

知识点2、哈希冲突和扩容

存在“多个输入对应相同输出”的情况，可以通过扩容哈希表来减少哈希冲突。

HELLO算法笔记之散列表（哈希）

类似于数组扩容，哈希表扩容需将所有键值对从原哈希表迁移至新哈希表，非常耗时。并且由于哈希表容量 capacity 改变，我们需要重新计算所有键值对的存储位置，进一步提高了扩容过程的计算开销。

「负载因子 Load Factor」是一个重要概念，其定义为哈希表的元素数量除以桶数量，为了衡量哈希冲突的严重程度，也常被作为哈希表扩容的触发条件。例如在 Java 中，当负载因子超过 0.75 时，系统会将哈希表容量扩展为原先的 2 倍。

二、哈希冲突

改良哈希表数据结构，使得哈希表可以在存在哈希冲突时正常工作。
仅在必要时，即当哈希冲突比较严重时，执行扩容操作。

哈希表的结构改良方法主要包括链式地址和开放寻址。

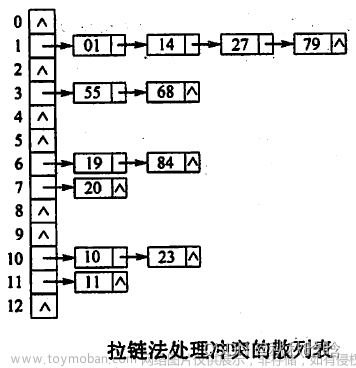
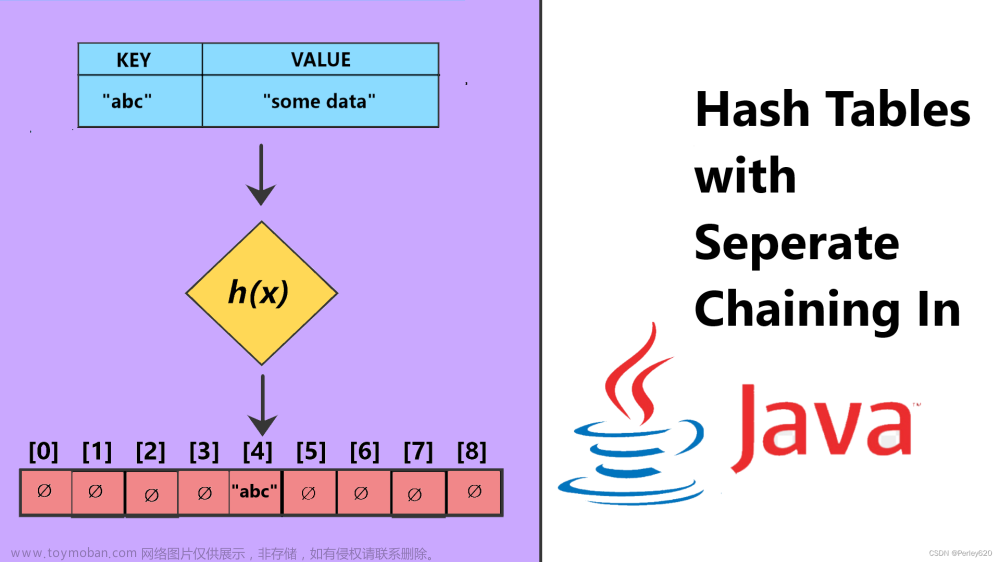
哈希表的结构改良方法一：链式地址

将单个元素转换为链表，将键值对作为链表节点，将所有发生冲突的键值对都存储在同一链表中。每个桶都是一个列表/链表

HELLO算法笔记之散列表（哈希）

查询元素：输入 key ，经过哈希函数得到数组索引，即可访问链表头节点，然后遍历链表并对比 key 以查找目标键值对。
添加元素：先通过哈希函数访问链表头节点，然后将节点（即键值对）添加到链表中。
删除元素：根据哈希函数的结果访问链表头部，接着遍历链表以查找目标节点，并将其删除。

哈希表的结构改良方法二：开放寻址

「开放寻址 Open Addressing」不引入额外的数据结构，而是通过“多次探测”来处理哈希冲突，探测方式主要包括线性探测、平方探测、多次哈希。

HELLO算法笔记之散列表（哈希）

线性探测存在以下缺陷：

不能直接删除元素。删除元素会在数组内产生一个空位，查找其他元素时，该空位可能导致程序误判元素不存在。因此，需要借助一个标志位来标记已删除元素。（查找的时候是遍历整个表的，如果遇到none就会返回不存在）（开放寻址法都会有不能直接删除元素的缺陷。）
容易产生聚集。数组内连续被占用位置越长，这些连续位置发生哈希冲突的可能性越大，进一步促使这一位置的“聚堆生长”，最终导致增删查改操作效率降低。

对哈希的解释：对 1 个对象进行 Hash，就可以得到这个对象的一个映射值，这个映射值其实就是 Hash 值，这值转换存到数组的某个位置中，就是放到桶中。

三、哈希算法

无论是开放寻址还是链地址法，它们只能保证哈希表可以在发生冲突时正常工作，但无法减少哈希冲突的发生。

一些简单的哈希算法：