1.乘法原理
二进制数乘法的显著特点就是可以将乘法转换为移位,乘2就是左移一位,乘2^n就是左移n位。而一个二进制数又可以看成是由若干个2的i次方的和。
设被乘数和乘数分别为M、N,且都是32位的二进制数,乘积结果为64位 的向量CO则

 。
。
所以乘法可以由移位电路和加法器完成。计算有两种方式:串行和并行。
串行计算是每进行一次移位,将结果相加,计算一次乘法总共需要n+1个时钟周期,n次移位和n次加法。
而并行则是需要两个时钟周期,n个移位电路分别移位之后,将n个结果相加。而第二个周期的n个数相加这一步会需要非常长的计算延时,导致电路时序(建立时间、保持时间)很难满足要求,且风险很高
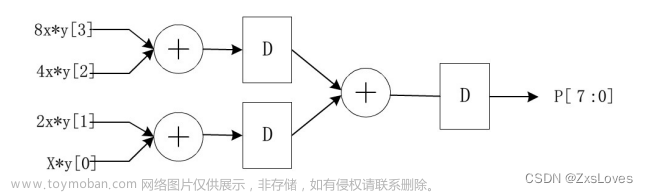
流水线乘法器则是在串行计算的基础上将每次移位和加法的结果暂存,并且第一级电路计算完成之后可以直接开始下一组数据的乘法计算。对于4位的数据乘法,在延迟后电路会源源不断地输出数据,而普通的并行方式的乘法器则是每两个周期计算一次乘法。
2.模块编写
2.1 底层模块multi_cell
首先我们需要设计一个底层模块用于输出移位和相加结果,并且加上valid和ready信号作为握手协议,valid拉高时输入数据有效
算法中每次被乘数M的移位都是递增,可以将4位的M先拓展成8位的{4'b0,M}作为multi_cell的输入,每级移位一次。对于N,虽然我们可以将N的每一位作为multi_cell的输入,但是这设计时就固定了电路适合的位数。比如4位的代码无法进行8位的计算,需要修改。
所以为了增加设计的通用性,我们将乘数N进行右移,每级移位一次并全部取第0位。当乘法器位宽改变时,只需要修改参数M、N即可。
需要多少级multi_cell由乘数N的位数决定, 对于第i级模块,输入为移位了i次的M,对应的是移位了i次的N,此时第0位即为原N的第i位。在计算加法时,如果移位后的N第0位是1,则上一级和与当前M相加,否则加0。(级数由0开始)
下面是multi_cell的verilog代码
module multi_cell #
(
parameter M = 4,
parameter N = 4
)
(
//input
clk,
rst_n,
multi_M,
multi_N,
multi_acci,
valid,
//output
multi_shift_M,
multi_shift_N,
multi_acco,
ready
);
input wire clk;
input wire rst_n;
input wire [M+N-1:0] multi_M;
input wire [N-1:0] multi_N;
input wire [N+M-1:0] multi_acci;
output reg [M+N-1:0] multi_shift_M;
output reg [N-1:0] multi_shift_N;
output reg [M+N-1:0] multi_acco;
//protocal
input wire valid;
output reg ready;
always @(posedge clk or negedge rst_n) begin
if(!rst_n)begin
ready <= 1'b0;
multi_shift_M <= {(M+N){1'b0}};
multi_shift_N <= {(N){1'b0}};
multi_acco <= {(M+N){1'b0}};
end
else if(valid)begin
ready <= 1'b1;
multi_shift_M <= (multi_M << 1);
multi_shift_N <= (multi_N >> 1);
if(multi_N[0])
multi_acco <= multi_acci + multi_M;
else
multi_acco <= multi_acci;
end
else begin
ready <= 1'b0;
multi_shift_M <= {(M+N){1'b0}};
multi_shift_N <= {(N){1'b0}};
multi_acco <= {(M+N){1'b0}};
end
end
endmodule2.2 顶层模块设计
顶层模块将multi_cell级联即可,将每一级输出的移位之后M的结果作为下一级被乘数的输入,N同理。acco作为下一级的acci。
需要注意的是第0级的acci为0.同时需要消耗寄存器储存每一次的输出(移位输出和acco)。并且由于握手协议的存在,每一级的ready信号作为下一级的valid,并且需要逐级储存,第一级的valid由输入决定,最后一级的ready和累加和连接到输出。
下面是multiplier的顶层代码文章来源:https://www.toymoban.com/news/detail-498215.html
`timescale 1ns/1ns
module multi_pipe#(
parameter M = 4,
parameter N = 4
)(
//input
clk,
rst_n,
multi_M,
multi_N,
valid,
//output
multi_o,
ready
);
input wire clk;
input wire rst_n;
input wire [M-1:0] multi_M;
input wire [N-1:0] multi_N;
input wire valid;
output wire [N+M-1:0] multi_o;
output wire ready;
wire [N+M-1:0] multi_shift_M [N-1:0];
wire [N+M-1:0] multi_shift_N [N-1:0];
wire [N+M-1:0] multi_acco [N-1:0];
wire [N-1:0] valid_array;
multi_cell#(
.M(M),
.N(N)
)
multi_cell_0(
.clk (clk ),
.rst_n (rst_n ),
.multi_M ({{N{1'b0}},multi_M}),
.multi_N (multi_N ),
.multi_acci ({(M+N){1'b0}} ),
.valid (valid ),
.multi_shift_M (multi_shift_M[0] ),
.multi_shift_N (multi_shift_N[0] ),
.multi_acco (multi_acco[0] ),
.ready (valid_array[0] )
);
genvar i;
generate
for(i=1;i<N;i=i+1)begin:multi_cell_x
multi_cell#(
.M(M),
.N(N)
)
multi_cell_x(
.clk (clk ),
.rst_n (rst_n ),
.multi_M (multi_shift_M[i-1] ),
.multi_N (multi_shift_N[i-1] ),
.multi_acci (multi_acco[i-1] ),
.valid (valid_array[i-1] ),
.multi_shift_M (multi_shift_M[i] ),
.multi_shift_N (multi_shift_N[i] ),
.multi_acco (multi_acco[i] ),
.ready (valid_array[i] )
);
end
endgenerate
assign multi_o = multi_acco[N-1];
assign ready = valid_array[N-1];
endmodule3.testbench验证
testbench如下所示,经过延迟后,持续输出数据文章来源地址https://www.toymoban.com/news/detail-498215.html

`timescale 1ns/1ps
module Top_tb #(
parameter M = 4,
parameter N = 4
)
();
reg clk;
reg rst_n;
reg data_rdy ;
reg [N-1:0] mult1 ;
reg [M-1:0] mult2 ;
wire res_rdy ;
wire [N+M-1:0] res ;
//driver
initial begin
clk = 0;
rst_n = 0;
#55 ;
rst_n = 1;
@(negedge clk ) ;
data_rdy = 1'b1 ;
mult1 = 25; mult2 = 5;
#10 ; mult1 = 16; mult2 = 10;
#10 ; mult1 = 10; mult2 = 4;
#10 ; mult1 = 15; mult2 = 7;
mult2 = 7; repeat(32) #10 mult1 = mult1 + 1 ;
mult2 = 1; repeat(32) #10 mult1 = mult1 + 1 ;
mult2 = 15; repeat(32) #10 mult1 = mult1 + 1 ;
mult2 = 3; repeat(32) #10 mult1 = mult1 + 1 ;
mult2 = 11; repeat(32) #10 mult1 = mult1 + 1 ;
mult2 = 4; repeat(32) #10 mult1 = mult1 + 1 ;
mult2 = 9; repeat(32) #10 mult1 = mult1 + 1 ;
#500 $stop;
end
//对输入数据进行移位,方便后续校验
reg [N-1:0] mult1_ref [M-1:0];
reg [M-1:0] mult2_ref [M-1:0];
always @(posedge clk) begin
mult1_ref[0] <= mult1 ;
mult2_ref[0] <= mult2 ;
end
genvar i ;
generate
for(i=1; i<=M-1; i=i+1) begin
always @(posedge clk) begin
mult1_ref[i] <= mult1_ref[i-1];
mult2_ref[i] <= mult2_ref[i-1];
end
end
endgenerate
//自校验
reg error_flag ;
always @(posedge clk) begin
# 1 ;
if (mult1_ref[M-1] * mult2_ref[M-1] != res && res_rdy) begin
error_flag <= 1'b1 ;
end
else begin
error_flag <= 1'b0 ;
end
end
//module instantiation
multi_pipe #(.N(N), .M(M))
uut
(
.clk (clk),
.rst_n (rst_n),
.valid (data_rdy),
.multi_M (mult1),
.multi_N (mult2),
.ready (res_rdy),
.multi_o (res)
);
always #5 clk = ~clk;
endmodule到了这里,关于流水线乘法器的原理及verilog代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!