中国矿业大学信控学院
补一下我之前在博客园发布的内容
懒得调了,想复制完整代码直接复制最下面的,想复制分布代码去看我博客园链接吧
《数据结构与算法分析》课程设计——迷宫问题 - 刷子zz - 博客园
一、 问题描述
问题中迷宫可用方阵[m,n]表示,0表示能通过,1表示不能通过。若要从从左上角[1,1]进入迷宫,设计算法,寻求一条从右下角 [m,n] 出去的路径。我们用递增的数来代表寻找出口方向与步数,用-2来代表寻找过程中找错的路径。
二、 需求分析
需要先创建一个迷宫,在开始后就开始搜寻,当一个点周围有0点(改点并不是以搜寻过的点),那么到这里继续往下搜,如果搜到尽头那么就要倒回去,在搜寻倒回去的周围还有为搜寻过得0点,因此需要一个存储算法,要满足后入先出,那么就是栈,利用栈就可以满足需求。
三、 算法分析
1. 首先先定义栈,本问题中,不需要在中间插入与弹出,插入与弹出操作均在栈头,因此我们利用顺序栈。
并且该栈与实验课的栈不同,因为要满足实际需求,所以我们需要定义步数以及改点所在的位置以及临近路径的位置在我们栈中,具体操作如下。

1 //记录通道块在迷宫矩阵当中的横、纵坐标
2 struct Position {
3 int x;
4 int y;
5 };
6
7 //放入栈当中的通道块元素
8 struct SElement {
9 int ord;//记录步数
10 Position p;//记录位置
11 int di;//记录下一次测试这一路径的临近路径的位置
12 };
13
14 struct MyStack {
15 SElement* base;
16 SElement* top;
17 int stacksize;
18 };

2. 栈的一些列基础操作,例如创建栈,判断栈是否为空,取栈顶元素,获取栈长,入栈,出栈。上述操作类似学校实验中基本操作,这里不在叙述,详见附录中全部代码。
3. 接下来创建迷宫,这里迷宫利用数组来生成,x轴为n,y轴为m
n为18,m为15。生成方法简单,这里不在叙述,详见附录中全部代码。
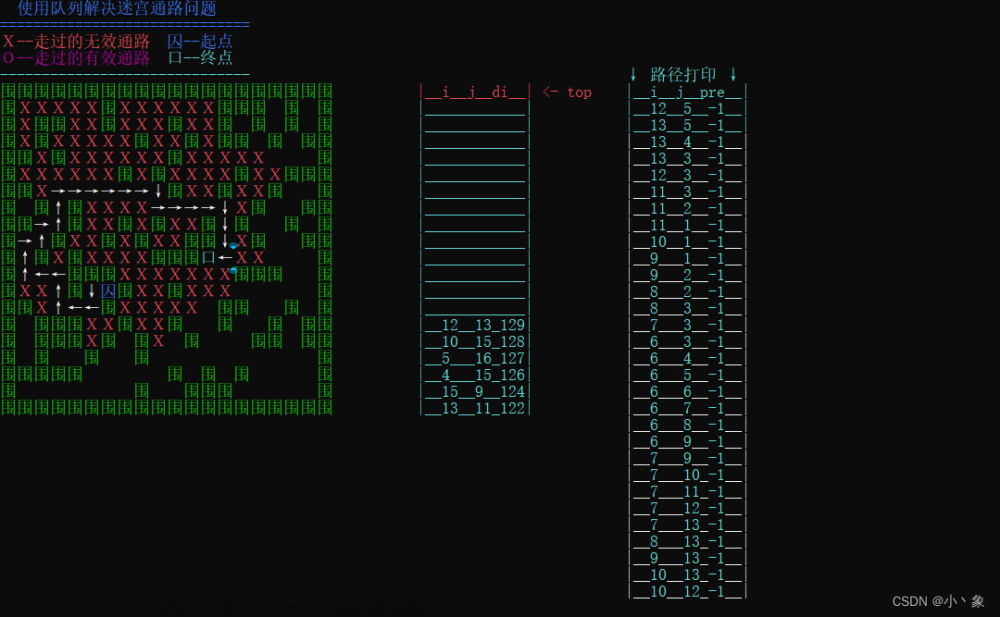
4. 接下来定义如何走这个迷宫,考虑我们用0作为通道,1作为墙壁,那么搜寻一个点的上下左右0就是可以通过,1就是不能通过。利用以下循环来完成目标:
步骤1:挪到0处的点并且把刚才位置入栈,让改点改为步数,让步数加一,然后继续搜索其上下左右(除去刚才通过的点)如果有0,继续执行步骤1。
步骤2:如果周围的点无0(除去刚才已经通过的点),让改点改为-2,那么就出栈,把路径调到刚才的那个点,并且把步数减一,然后执行步骤1,搜寻其上下左右(出去刚才走错的点以及入这个点之前的点)。
直至入栈点是终点那么退出循环。
代码如下:

1 do
2 {
3 if (Pass(curp))
4 {
5 FootPrint(curp, curStep);//可走就在迷宫里面留下足迹
6 //创建一个栈元素,存储可行路径的相关值
7 SElement e;
8 e.di = 1;// 下一个路块为这一个路块的右边的路块
9 e.ord = curStep;
10 e.p.x = curp.x;
11 e.p.y = curp.y;
12 Push(&path, e);//将路径块入栈
13 if (curp.x == m - 2 && curp.y == n - 2) break; //如果被压入的路径块到了迷宫的终点就退出循环
14 //找到下一个被试块
15 curp = NextPosition(curp, 1);//找到前一个被试块东面的路径块作为被试块
16 curStep++;//被探索的步数加一
17 }
18 else//如果当前被试路径不能够通过的话
19 {
20 if (!IsStackEmpty(&path))
21 {
22 SElement e;
23 Pop(&path, &e);
24 curStep--;
25 //将这一段所有的周围路径都已经被测试过的路径从栈中清除
26 while (e.di == 4 && !IsStackEmpty(&path)) {
27 MarkPrint(e.p);
28 Pop(&path, &e);
29 curStep--;
30 }
31 //如果当前栈顶还有未被测试的路径就测试剩余的周围路径
32 if (e.di<4)
33 {
34 curp = NextPosition(e.p, e.di + 1);
35 e.di++;
36 curStep++;
37 Push(&path, e);
38 }
39 }
40 }
41 } while (!IsStackEmpty(&path));

5. 在定义上述代码中如何去搜寻,按照从右到下再到左再到上的方法搜寻。代码如下:

1 //按顺时针方向从右开始寻找矩阵当中某一个位置的临近位置
2 Position NextPosition(Position now, int direction)
3 {
4 Position next;
5 int x = now.x;
6 int y = now.y;
7 switch (direction)
8 {
9 //右
10 case 1: {
11 next.x = x;
12 next.y = y + 1;
13 break;
14 }
15 //下
16 case 2: {
17 next.x = x + 1;
18 next.y = y;
19 break;
20 }
21 //左
22 case 3: {
23 next.x = x;
24 next.y = y - 1;
25 break;
26 }
27 //上
28 case 4:{
29 next.x = x - 1;
30 next.y = y;
31 break;
32 }
33 default:break;
34 }
35 return next;
36}

6. 定义是否可以通过函数,是就返回ture不是就返回false。代码如下:

1 //辅助函数考察当前路径能否通过
2 bool Pass(Position posi)
3 {
4 //只有路径所在位置的数字为0的是可以走的
5 if (Maze[posi.x][posi.y] == 0)
6 {
7 return true;
8 }
9 return false;
10 }

7. 定义是入栈和出栈时如何修改迷宫数组中的值。代码如下:

1 //改变改点为步骤数
2 void FootPrint(Position p, int step)
3 {
4 Maze[p.x][p.y] = step;
5 }
6
7 //路径不可走的话就留下-2的标记
8 void MarkPrint(Position p)
9 {
10 Maze[p.x][p.y] = -2;
11}

8. 定义打印迷宫函数,这个就是遍历整个数组,过程简单这里不在叙述,见附录中全部代码。
四、 结论
编辑ing...
五、 参考文献
[1] 严蔚敏,吴伟民——《数据结构》清华大学出版社2004.2.1
六、 附录文章来源:https://www.toymoban.com/news/detail-498670.html
完整代码如下:文章来源地址https://www.toymoban.com/news/detail-498670.html
#include <stdio.h>
#include <malloc.h>
#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10
//记录通道块在迷宫矩阵当中的横、纵坐标
struct Position {
int x;
int y;
};
//放入栈当中的通道块元素
struct SElement {
int ord;//记录步数
Position p;//记录位置
int di;//记录下一次测试这一路径的临近路径的位置
};
struct MyStack {
SElement* base;
SElement* top;
int stacksize;
};
//创建一个栈如果创建成功则返回1,否则就返回0
int InitStack(MyStack* s)
{
s->base = (SElement*)malloc(STACK_INIT_SIZE * sizeof(SElement));//为栈分配初始空间
if (!s->base) return 0;
s->top = s->base;//设定为空栈
s->stacksize = STACK_INIT_SIZE;
return 1;
}
//判断栈是否为空,如果是空的就返回0,否则就返回1
int IsStackEmpty(MyStack* s)
{
if (s->top == s->base) return true;
return false;
}
//获取栈顶元素,如果栈为空就返回0 否则就返回1
int GetTop(MyStack* s, SElement* e)
{
if (IsStackEmpty(s)) return 0;
e = s->top - 1;
return 1;
}
//获取栈的长度,并且通过程序返回
int StackLength(MyStack* s)
{
return s->top - s->base;
}
//插入元素e为新的栈顶元素,插入成功则返回1,否则返回0
int Push(MyStack* s, SElement e)
{
if (s->top - s->base >= STACK_INIT_SIZE)
{
s->base = (SElement*)realloc(s->base, (s->stacksize + STACKINCREMENT) * sizeof(SElement));
if (!s->base) return 0;
s->top = s->base + s->stacksize;
s->stacksize += STACKINCREMENT;
}
*(s->top) = e;
s->top++;
return 1;
}
//弹出栈顶元素赋值给e弹出成功返回1,弹出失败返回0
int Pop(MyStack* s, SElement* e)
{
if (IsStackEmpty(s)) return 0;
*e = *(s->top - 1);
s->top--;
return 1;
}
//定义墙元素为1 可走路径为0 已知路径为curStep 不能够通过的路径为-2
#define m 15
#define n 18
int Maze[m][n] = { { 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 },
{ 1,0,0,0,1,0,0,1,0,0,0,0,0,0,0,0,0,1 },
{ 1,0,1,1,1,0,1,0,0,1,0,1,1,1,1,1,0,1 },
{ 1,0,1,1,1,0,1,0,1,1,0,1,0,1,1,0,0,1 },
{ 1,0,0,0,0,0,1,0,1,1,0,1,0,0,0,0,1,1 },
{ 1,1,1,1,0,0,1,0,1,1,0,1,1,1,1,0,1,1 },
{ 1,1,1,0,0,1,1,0,1,1,0,0,0,1,1,1,1,1 },
{ 1,1,1,0,1,1,1,0,1,1,1,1,0,1,1,0,0,1 },
{ 1,1,1,0,0,0,0,0,0,0,1,1,0,1,1,0,1,1 },
{ 1,0,0,1,1,1,1,1,1,0,1,1,0,1,0,0,1,1 },
{ 1,1,0,0,0,0,0,0,0,0,1,0,0,1,0,1,1,1 },
{ 1,0,0,1,0,1,0,1,0,0,1,1,0,0,0,1,1,1 },
{ 1,1,0,1,0,1,0,1,1,1,0,0,0,1,1,1,1,1 },
{ 1,1,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,1 },
{ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 } };
//辅助函数考察当前路径能否通过
bool Pass(Position posi)
{
//只有路径所在位置的数字为0的是可以走的
if (Maze[posi.x][posi.y] == 0)
{
return true;
}
return false;
}
//按顺时针方向从右开始寻找矩阵当中某一个位置的临近位置
Position NextPosition(Position now, int direction)
{
Position next;
int x = now.x;
int y = now.y;
switch (direction)
{
//右
case 1: {
next.x = x;
next.y = y + 1;
break;
}
//下
case 2: {
next.x = x + 1;
next.y = y;
break;
}
//左
case 3: {
next.x = x;
next.y = y - 1;
break;
}
//上
case 4:
{
next.x = x - 1;
next.y = y;
break;
}
default:break;
}
return next;
}
//改变改点为步骤数
void FootPrint(Position p, int step)
{
Maze[p.x][p.y] = step;
}
//路径不可走的话就留下-2的标记
void MarkPrint(Position p)
{
Maze[p.x][p.y] = -2;
}
//打印出迷宫矩阵
void Display_migong()
{
for (int i = 0; i<m; i++)
{
for (int j = 0; j<n; j++)
{
if (Maze[i][j]<0)
printf("%d ", Maze[i][j]);
else if (Maze[i][j]<10)
printf("%d ", Maze[i][j]);
else
printf("%d ", Maze[i][j]);
}
printf("\n");
}
}
int main()
{
//迷宫程序主体
MyStack path;//记录路径的栈
InitStack(&path);//初始化路径数组
Position curp;//当前被试位置
Display_migong();
//初始化当前位置为矩阵入口
curp.x = 1;
curp.y = 1;
int curStep = 1;//被探索的步数
do
{
if (Pass(curp))
{
FootPrint(curp, curStep);//可走就在迷宫里面留下足迹
//创建一个栈元素,存储可行路径的相关值,将这个元素存储到栈当中
SElement e;
e.di = 1;//下一个路块为这一个路块的右边的路块
e.ord = curStep;
e.p.x = curp.x;
e.p.y = curp.y;
Push(&path, e);//将路径块入栈
if (curp.x == m - 2 && curp.y == n - 2) break; //如果被压入的路径块到了迷宫的终点就退出循环
curp = NextPosition(curp, 1);//找到前一个被试块东面的路径块作为被试块
curStep++;//被探索的步数加一
}
else//如果当前被试路径不能够通过的话
{
if (!IsStackEmpty(&path))
{
SElement e;
Pop(&path, &e);
curStep--;
//将所有的周围路径都已经被测试过的路径从栈中清除
while (e.di == 4 && !IsStackEmpty(&path)) {
MarkPrint(e.p);
Pop(&path, &e);
curStep--;
}
//如果当前栈顶还有未被测试的路径就测试剩余的周围路径
if (e.di<4)
{
curp = NextPosition(e.p, e.di + 1);
e.di++;
curStep++;
Push(&path, e);
}
}
}
} while (!IsStackEmpty(&path));
printf("\n");
//打印出结果迷宫矩阵
Display_migong();
return 0;
}到了这里,关于《数据结构与算法分析》课程设计——迷宫问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!

![【Python数据结构与算法】--- 递归算法的应用 ---[乌龟走迷宫] |人工智能|探索扫地机器人工作原理](https://imgs.yssmx.com/Uploads/2024/02/752756-1.gif)




