神经网络：初始化-Toy模板网

这篇具有很好参考价值的文章主要介绍了神经网络：初始化。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

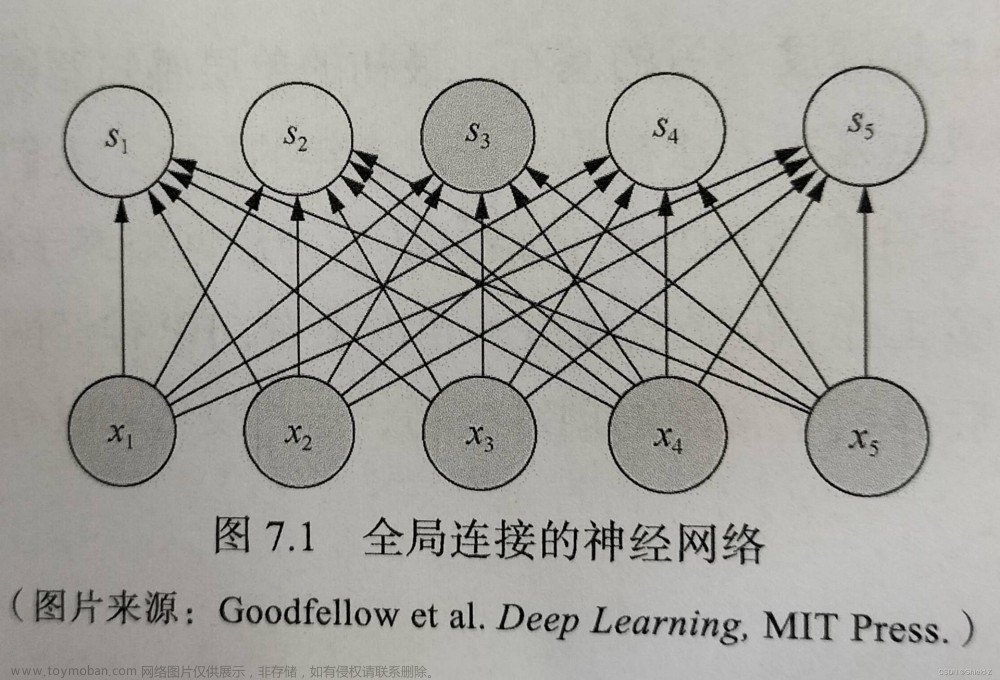
初始化在计算机视觉中是指对神经网络模型的参数进行初始赋值的过程。它的作用是为模型提供一个良好的起点，以便更快地收敛到较好的解，并避免梯度消失或梯度爆炸等问题。以下是从数学角度解释初始化的原理和意义：

原理：
神经网络的参数通常以矩阵的形式表示，如权重矩阵。初始化的过程就是为这些参数矩阵赋予初始值。在神经网络中，每个参数都会参与前向传播和反向传播的计算过程。如果参数的初始值过小或过大，就有可能导致梯度在反向传播过程中逐渐消失或爆炸，从而影响模型的训练效果。

意义：
适当的初始化可以提高模型的训练效率和性能，具体包括以下几个方面：

避免梯度消失和梯度爆炸：
初始化可以避免梯度在反向传播过程中过早地变得非常小或非常大，导致梯度消失或梯度爆炸的问题。这样可以使模型更容易学习和更新参数，提高模型的稳定性和收敛速度。
提高模型的表达能力：
适当的初始化可以帮助模型更好地表达数据的复杂性。通过合理地初始化参数，可以为模型提供一定的学习能力和表达能力，使其能够更好地适应训练数据和提取有效的特征。
防止陷入局部最优解：
初始化可以影响模型收敛到的解的质量。合适的初始化可以使模型具有足够的多样性，避免陷入局部最优解，并提高模型的泛化能力。

数学角度上，初始化的原理涉及参数的分布和尺度。一种常用的初始化方法是使用均匀分布或正态分布来随机初始化参数。具体来说，对于均匀分布，参数的初始值从一个给定的范围内随机选择；对于正态分布，参数的初始值根据给定的均值和标准差进行随机采样。这样的初始化方法可以使参数在合理的范围内进行初始化，有助于避免梯度消失和梯度爆炸，并提供良好的起点来优化模型。

在神经网络中，常见的参数初始化方法包括以下几种：

零初始化（Zero Initialization）：
- 公式： $W = 0$
- 含义：将参数矩阵 $W$ 的所有元素初始化为零。
- 方法：将所有参数初始化为零。
- 优点：简单快速，适用于某些特定场景，如输出层的偏置初始化。
- 缺点：无法破坏对称性，可能导致模型难以学习。
随机初始化（Random Initialization）：
- 均匀分布：
  - 公式： $\sim U(-a, a)$
  - 含义：使用均匀分布在区间 $(- a, a)$ 上随机初始化参数矩阵 $W$ 。 $U (a, b)$ 表示均匀分布， $a$ 表示分布的最小值， $b$ 表示分布的最大值。
- 方法：使用随机数初始化参数，常用的方式包括均匀分布和正态分布。
- 优点：打破对称性，使得模型能够更好地学习和表达。
- 缺点：需要根据具体情况选择合适的分布和参数范围。
Xavier 初始化（Xavier Initialization）：
- 公式： $\sim N\left(0, \frac{1}{n_{\text{in}}}\right)$
- 含义：使用均值为零、方差为 $\frac{1}{n_{\text{in}}}$ 的正态分布随机初始化参数矩阵 $W$ 。 $n_{\text{in}}$ 表示输入维度。
- 方法：根据输入和输出维度自适应地选择参数的初始化范围。
- 优点：适用于激活函数为 sigmoid 或 tanh 的情况，有助于避免梯度消失或梯度爆炸。
- 缺点：在 ReLU 激活函数下表现可能不佳。
He 初始化（He Initialization）：
- 公式： $\sim N\left(0, \frac{2}{n_{\text{in}}}\right)$
- 含义：使用均值为零、方差为 $\frac{2}{n_{\text{in}}}$ 的正态分布随机初始化参数矩阵 $W$ 。 $n_{\text{in}}$ 表示输入维度。
- 方法：根据输入维度自适应地选择参数的初始化范围。
- 优点：适用于激活函数为 ReLU 或其变体的情况，有助于避免梯度消失或梯度爆炸。
- 缺点：在 sigmoid 或 tanh 激活函数下表现可能不佳。

这些初始化方法的选择和使用要根据具体的网络架构、激活函数以及任务需求进行调整。没有一种初始化方法适用于所有情况，因此在实践中需要通过实验和调优来确定最佳的初始化策略。一般而言，这些初始化方法适用于各种计算机视觉任务和环境，包括图像分类、目标检测、语义分割等。具体的选择和调整应基于模型的架构和激活函数的选择，以及任务的特点和数据的分布等因素。需要注意的是，实际应用时可能会根据具体情况进行微调和改进。

以下是使用PyTorch框架实现每种初始化方法的示例代码：

零初始化（Zero Initialization）：

import torch.nn as nn

# 定义模型
model = nn.Sequential(
    nn.Linear(in_features, out_features),
    nn.Zero_(weight)  # 零初始化
)

随机初始化（Random Initialization）：

import torch.nn.init as init

# 定义模型
model = nn.Sequential(
    nn.Linear(in_features, out_features),
)
# 随机初始化
init.uniform_(model[0].weight, a=-0.1, b=0.1)  # 均匀分布初始化
# 或者
init.normal_(model[0].weight, mean=0, std=0.01)  # 正态分布初始化

Xavier 初始化（Xavier Initialization）：

import torch.nn.init as init

# 定义模型
model = nn.Sequential(
    nn.Linear(in_features, out_features),
)
# Xavier 初始化
init.xavier_normal_(model[0].weight)  # 正态分布初始化
# 或者
init.xavier_uniform_(model[0].weight)  # 均匀分布初始化

He 初始化（He Initialization）：

import torch.nn.init as init

# 定义模型
model = nn.Sequential(
    nn.Linear(in_features, out_features),
)
# He 初始化
init.kaiming_normal_(model[0].weight)  # 正态分布初始化
# 或者
init.kaiming_uniform_(model[0].weight)  # 均匀分布初始化

请注意，在示例代码中，in_features表示输入特征的维度，out_features表示输出特征的维度。初始化方法的具体调用使用了PyTorch的init模块，其中的函数根据需要进行选择。这些示例代码可以在实际搭建神经网络时使用，根据网络架构和初始化需求进行相应的调整。文章来源地址https://www.toymoban.com/news/detail-498910.html

到了这里，关于神经网络：初始化的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！