密码学概念科普（加密算法、数字签名、散列函数、HMAC）-Toy模板网

这篇具有很好参考价值的文章主要介绍了密码学概念科普（加密算法、数字签名、散列函数、HMAC）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

密码散列函数

密码散列函数 (Cryptographic hash function)，是一个单向函数，输入消息，输出摘要。主要特点是：

只能根据消息计算摘要，很难根据摘要反推消息
改变消息，摘要一定会跟着改变
对于不同的消息，计算出的摘要几乎不可能相同

根据散列函数的上述特点，可以应用在保存密码、数据防篡改和完整性保护、数字签名等方面，后面介绍其他概念的时候也会提到。

在网上下载文件时，经常会提供 MD5 值供校验。因为文件实际可能是从世界各地的镜像站下载的，有可能会被篡改，所以下载完成之后计算一下 MD5 看是否一致，就知道是否被篡改了。

一般系统在设计时，都不会直接保存密码原文，防止密码泄漏。这时可以使用散列函数保存原始密码的摘要。根据散列函数的特点，即便摘要泄漏了，也很难反推出密码是什么。只有正确的输入了原始密码，才能计算出完全相同的摘要。

虽然散列函数是单向的，但可以使用彩虹表用空间换时间。就是把常见的组合的摘要都计算出来，这样拿到一个摘要之后，去比对一下就有可能找到原始信息。例如可以去搜索引擎上搜索一下 456b7016a916a4b178dd72b947c152b7 这个字符串，很容易就能知道他的原文是什么。

为了避免被彩虹表攻击，可以在计算摘要时，添加一点随机的东西进去再计算摘要，这个东西叫盐值 (salt)。由于盐值足够长且是随机的，这样想通过事先计算的彩虹表去碰撞就会更困难了。例如上面那个字符串很容易能搜到是 admin 的 MD5 值。而如果我们给 admin 后面拼接上 P6R8ERaZ，再计算出 adminP6R8ERaZ 的 MD5 值 70a1a6831709d7e7cb6cc35ccdfdbd39，再去搜索这个值就很难找到他的原文了。上面只是个例子，实际应用中，盐值不是简单的添加到原始消息的后面。

常见的散列函数包括 MD5、SHA-1、SHA-2 等。SHA-2 包含 SHA-256/224、SHA-512/384 等。其中 MD5、SHA-1 已经被证明不安全，推荐使用 SHA-2 系列的。

本文的例子中都使用 MD5，是因为 MD5 生成的摘要是 128 位的，更短一点好写。

MAC/HMAC

上面提到下载文件时可能会提供文件的 MD5，供校验文件是否被篡改。这样做有个前提是这个 MD5 本身不会被篡改。例如下载的文件放在镜像站，而 MD5 本身是放在 HTTPS 的源网站的。

但很多时候摘要本身也是不能安全传递的，这时如果还使用摘要去校验就失去了意义，因为篡改消息的人直接把摘要一起篡改了就行了。

这种情况可以使用消息认证码 (Message authentication code, MAC)。MAC 是根据一个密钥，使用一个算法，把消息计算成一个摘要。通信的另一方，使用相同的密钥和算法，计算出摘要，对比是否一致，可以验证消息是否被篡改。

将消息和 MAC 一起传递，如果消息被篡改了，但中间人没有密钥，无法计算出新的 MAC，消息接收方就能校验出消息被篡改了。

举个例子，我们可以定义这样一个 MAC 算法：原始消息后面直接拼接密钥，然后使用 MD5 算法计算摘要。假设通信双方约定的密钥是 secret。当我要发送 Hello World 时，就计算出 Hello Worldsecret 的 MD5 值 (88266e1db8f6446d33071e6b1b14747f) 作为 MAC 一起发送。如果有人截获了这个消息删了一个字母变成了 Hello Worl，他不知道我们约定的密钥 secret，就没办法计算出新的 MAC。接收方收到 Hello Worl 拼接上 secret 计算出的 MAC 是 d5f4677a2612e26c50b55ba257743170，就会发现消息被篡改了。

这只是个例子，实际的 MAC 算法是一定不能直接把消息和密钥拼接起来计算摘要的，容易受到长度扩展攻击。

通常使用的 MAC 算法是 HMAC (keyed-hash message authentication code)，也就是使用密码散列函数去计算摘要。HMAC 算法对具体的散列函数没有限制，所以使用时需要明确使用的是哪个散列函数，例如 HMAC-MD5、HMAC-SHA256 等。

OTP

因为大多数用户设置的密码强度可能不够高，又或者可能在不安全的环境登陆过导致密码已经泄漏了。所以很多网站除了密码之外还需要其他验证方式，提高安全性。

这个时候就需要使用一些只有你和网站之间知道的信息来验证，而且这个信息最好是一次性的，避免被人截获之后可以多次用于验证。这个就是 OTP (one-time password)。

例如很多网站都会发送短信验证码或邮箱验证码，这个就属于一种 OTP。只有网站知道你的手机号和随机生成的验证码是什么，也只有你拥有这个手机号才能收到这个验证码，这个验证码用一次就会失效。

HOTP

使用短信验证码、邮箱验证码作为 OTP，还得依赖邮件服务商或者通信运营商等，而且没办法离线。

根据前面提到的 HMAC 的概念，我们可以在注册账号的时候和网站约定好一个密钥，这个密钥只需要在第一次生成的时候传递一次，双方都保存好。以后需要使用 OTP 验证的时候，我们就都用这个密钥去计算某个消息的 HMAC 值，用这个值作为 OTP 去做认证。这就是 HOTP (HMAC-based one-time password)。

使用 HOTP 同样可以达到验证的目的，还可以离线，不用依赖短信和邮箱服务器了。

TOTP

使用 HOTP 时，双方共同用于计算摘要的信息可以是一个计数器，例如初始时双方都是加密 1，每用一次就递增。但是这个计数器可能出现双方不一致的情况，所以可能还需要调整一下。

我们可以更进一步约定双方都去计算一个公开的信息的摘要，这个信息双方永远都会是一致的，会更方便一些。这个信息还要随时间变化，否则每次计算出来的摘要是同一个，就不是 OTP 了。既然这样，那直接把时间作为信息去计算摘要就好了，这就是 TOTP (Time-based one-time password) 了。

当然我们还要稍微做些变通，如果直接把精确到秒的时间作为信息去计算摘要，还没等输入呢，就已经过期了。所以一般都会有一个余量，比如除以 30 秒并向下取整，这样每 30 秒内计算出来的结果都是相同的。

HOTP 和 TOTP 都是有公开的标准的，规定了密钥是怎么编码的、使用哪种 HASH 函数、有效期是多长时间、生成的数字是几位的等等。按照这个标准，理论上自己手敲计算器都能计算出相同的 TOTP 值。要备份也很容易，只要把前面说的那个和网站约定的共同的密钥备份下来就行了。

国外主流网站都支持使用 TOTP 作为二次验证的手段，Google 和微软也都有自己的身份认证器应用。因为 TOTP 是一个标准，所以不是一定要用这些应用，更不是每个网站都要安装一个 APP。可以找一个支持 TOTP 的 APP 统一管理所有网站的就可以了。例如 Keepass，支持所有平台，还可以管理密码。

有些银行的安全介质除了 U 盾外，还有一种长得像一个小计算器一样的电子密码器，其实这个东西也算是一个 TOTP 和 HOTP 的应用。这个东西打开之后就会有一个每 30 秒更换一次的 6 位数字，办理业务时需要把这个数字输入进去，这就是 TOTP。有些场景还需要把网银或手机银行上弹出的几位数字输入到电子密码器中，然后再把密码器上生成的数字输入回网银或手机银行，这就是 HOTP。这里面的软件算法应该和上面说的差不多，做成一个硬件可以防止密钥泄漏、丢失。

对称加密算法

如果想加密一段信息，最容易想到的方式就是先随机生成一段足够长的密钥，例如 01010101011010101，然后用这个密钥对明文的每一位做异或操作，就得到了密文。如果这个密钥足够随机，理论上没有人能根据密文直接还原明文。解密时使用密钥再对密文做一次异或操作，就得到了明文。这基本上就是流加密的原理了。

这种需要加密和解密双方具有相同信息（密钥）的加密算法，叫做对称加密算法。

流加密就像上面例子一样，直接对每一位加密，效率高。但需要密钥和加密的数据一样长，很难做到，实际应用并不多。

另一种更常用的对称加密算法是分组加密算法，又叫块加密，就是把明文根据算法和密钥长度分成一块一块的去加密。

因为明文不太可能总是密钥长度的整数倍，所以不够的部分就需要填充，比如全填 0，或者按照其他什么规则填充，这个叫做填充模式。推荐使用的填充模式是 CMS (Cryptographic Message Syntax)。

分组加密处理每组数据有几种不同的工作模式。最直观的就是把每一块独立加密再拼接起来就行了，这就是 ECB 模式（Electronic codebook，电子密码本）。但这样的特征很容易被人识别。更安全一点的例如 CBC 模式（Cipher-block chaining，密码分组链接），每一块都是在上一块加密的基础上进行加密的。目前推荐使用的是 GCM 模式（Galois/Counter Mode，伽罗瓦/计数器模式）。

另外为了保证相同的明文多次加密的结果不一样，还要使用一个随机生成的初始化向量 (IV)，作用就跟盐值的作用差不多。

使用 OpenSSL 时，可以通过参数设置加密算法和工作模式，如果不指定默认是 CBC 模式。GPG 默认使用的是定制过的 CFB 模式，不能自己选择。

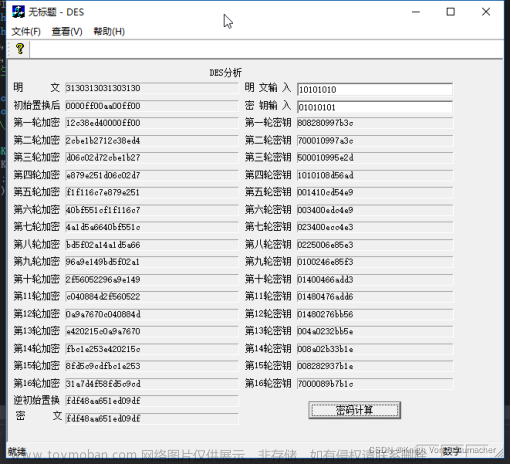
常见的对称加密算法有 DES、3DES、AES。其中 DES 已经不安全了，3DES 也不完全安全。建议使用 AES，AES 算法的密钥长度有 128、192、256 三种。

KDF/PBKDF2

我们在实际使用对称加密算法时，自己想的密码的强度通常是不够的。

例如 AES 算法最短的密钥长度也有 128 位，也就是 16 个字节，粗略的估计大概是 16 个字符的密码长度。实际不能这样比较，因为 128 位的密钥意味着有 2^128 ≈ 3 * 10^38 种组合的可能。而 16 个字符的密码，如果只包含字母和数字，大概只有 (26 + 26 + 10)^16 ≈ 5 * 10^28 种组合，就算算上全部 ASCII 可打印字符，也只有 95^16 ≈ 4 * 10^31 种组合。而且实际使用中，一般人不可能真的想到和记住这么复杂的密码。

所以如果直接使用自己想到的密码作为密钥去加密数据，实际暴力破解起来的难度至少会下降几个数量级，根本达不到 128 位的密钥强度。

为了解决这个问题，我们可以基于输入的密码去派生出一个更加安全的密钥。这个派生的过程要足够的慢、足够的随机。足够随机是为了防止被彩虹表攻击、足够的慢是增加暴力破解的难度。

例如本来 1 毫秒就能试一个密码，如果是 6 位数字的密码，只需要不到两分钟就能破解出来了。而如果这个密钥派生的过程需要 1 秒，那么同样是 6 位数字的密码，也需要大概 69 天才能试出来。

用于派生密钥的函数叫做 KDF (Key derivation function)，目前常用的是 PBKDF2 (Password-Based Key Derivation Function 2)。通过加入随机的盐值，使用 HMAC 算法，迭代很多轮次，得到最终的密钥。

另外前面提到的密码使用散列函数保存时，除了加盐外，一般也会使用 KDF，否则太容易被暴力破解。

GPG 的 s2k (string to key) 系列参数，就是用来控制 KDF 算法的相关参数。SSH 用的是 bcrypt pbkdf。OpenSSL 可以在命令中指定 pbkdf 算法和迭代次数。

非对称加密算法

根据 GPG 使用指南中的描述，直接使用对称加密算法加密，很多时候如何交换密钥就成了一个问题。而非对称加密则利用一些数学问题，使双方可以不需要具有相同的密钥也能加解密消息。

非对称加密算法一般利用的是离散对数、大数分解、椭圆曲线等数学问题。不管是哪个都超出了我的知识范畴，但这不影响我们理解非对称加密。

我们可以假设这是一个只会计算乘法、没人会算除法的世界。那么如果有这样一对数字 2 和 0.5，就可以把他们分别作为公钥和私钥。例如我可以把 2 作为公钥广而告之，谁想给我发送数字（例如 5），就把它乘 2 （得到 10）发过来，我收到之后再乘 0.5 就得到了原始数字（5）。而如果其他人拿到这个 10，即便知道公钥是 2，但是因为不会计算除法，所以也无法计算出原始数字。

正是因为非对称算法利用了各种数学计算，所以没有对称加密算法那种简单粗暴的位运算高效，性能大概比对称加密算法慢 10 倍以上。

所以一般不会直接使用非对称加密算法去加密原始信息，而是去加密一个短一点的对称加密密钥，然后再用这个对称加密密钥去加密真正的消息。当然理论上说，结合分组加密算法的工作模式，使用非对称加密算法直接去加密长一点的原始信息也是完全可行的，只是慢了点。

非对称加密算法的用途很广泛，除了基本的加密之外，还可以用于数字签名、密钥协商等场景。

数字签名

如果直接使用私钥加密，同样也只有公钥能解密。但因为公钥已经广而告之了，这种加密就没有保密的意义了。但可以证明这个消息确实是由这个持有这个公钥对应的私钥的人发出的，而且没有被改动过。就像是签名一样，所以叫做数字签名。

同样的基于性能的考虑，一般不会、也没必要用私钥直接加密（签名）整个消息。根据前面密码散列函数的特点，我们只需要先对消息计算个摘要，再对摘要进行签名，就可以达到给整个消息签名相同的效果了。

这就有点像要给一打文件盖章，没必要一页一页的去盖章，可以在这一打文件的侧面盖一个章。这样如果这一打文件被抽走、添加、替换了一页，这个印章都不会完整了。

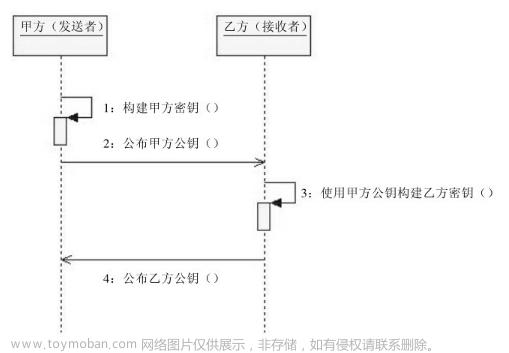
密钥协商

前面说了出于性能的考虑，我们一般只用非对称加密算法加密一个对称加密密钥，然后再用这个对称加密密钥去真正的加密消息。这种方式生成的密钥不够随机，只有通信的发送方参与了密钥的生成。密钥协商算法可以使通信的双方共同参与协商出一个密钥。

我们同样可以假设这是一个只会算乘法的世界，然后通信的双方可以事先约定好一个数字（例如 10），然后双方都再随机生成一个谁都不知道的数字（例如双方分别是 2 和 3），然后双方都用自己随机生成的数字乘以约定好的数字发给对方（10 * 2 = 20 和 10 * 3 = 30），双方收到后再都用收到的数字乘以自己随机生成的数字（30 * 2 = 60 和 20 * 3 = 60）就得到了相同的数字（60）作为密钥。最终生成的这个密钥双方都有参与，而其他人就算拿到了中间传递的 10、20、30 等信息，但因为他们都不会计算除法，就没办法知道真正的密钥是什么。

这种密钥协商算法可以安全的交换一个密钥，但没办法防止中间人攻击，所以一般使用时还需要结合数字签名等使用。

非对称加密算法概览

非对称加密算法的种类比较多，而且不像对称加密算法中 AES 一枝独秀，各种算法都有其使用场景，因此分别简单介绍一下。

依赖大数分解问题的算法：

RSA 算法是非对称加密算法中最主流、使用范围最广、兼容性最好的。安全性随着其密钥长度的增加而增加，但性能也会随之急剧下降。

依赖离散对数问题的算法：

DSA (Digital Signature Algorithm) 算法顾名思义，他在设计上就只是用来签名的，不能用来加密。
DH 密钥协商算法/协议，可以在通信的双方之间安全的交换会话密钥。

依赖椭圆曲线问题的概念：

ECC（Elliptic Curve Cryptography，椭圆曲线算法），比 RSA、DSA 等依赖大数分解和离散对数的算法性能更好。同等安全级别需要的密钥长度也更短。ECC 是一个泛指，并不是一个具体的算法。
ECDSA 是使用椭圆曲线实现的 DSA 算法的变体，具有比 DSA 算法更高的安全性和更好的性能。
EdDSA 和 ECDSA 类似，但使用的是爱德华兹曲线，比 ECDSA 性能和安全性更好。
ECDH 是使用椭圆曲线实现的 DH 密钥交换算法。

ECDSA、EdDSA、ECDH 和 ECC 一样，都是一种泛指，要结合具体的椭圆曲线实现。

具体的椭圆曲线：

NIST P-256/P-384/P-521，由 NIST 提供，但因为参数的来源不够透明，被质疑可能会有后门。
Brainpool P-256/P-384/P-512，参数更透明，但性能不如 NIST 的曲线。
Curve25519/Curve448，性能最好，参数更透明，没有专利限制等。

具体的椭圆曲线算法：

X25519 是使用了 Curve25519 曲线的 ECDH 算法实现。
Ed25519 是使用了 Curve25519 曲线和 SHA-512 的 EdDSA 算法实现。

非对称加密算法对比

这么多非对称加密算法，抛开只能用于密钥协商的 DH 和只能用于数字签名的 DSA，其实剩下的主要就是依赖大数分解问题的 RSA 算法和依赖椭圆曲线问题的 ECC 系列算法了。

更具体一点，我们可以对比一下 Curve25519 和 3072 位的 RSA 算法。

在安全方面，Curve25519 的密钥长度是 256 位，和 3072 位的 RSA 算法一样，都大概等同于 128 位的密钥强度。所以他们从安全性上来讲，基本上是相同的。

在性能方面，ECC 算法所需的密钥长度更短、计算性能更快。而且随着对安全级别要求的提升，ECC 的密钥长度是线性增加的、而 RSA 并不是。例如要实现 256 位的密钥强度，ECC 只需要 256 位密钥长度，RSA 算法则需要 15360 位。所以普遍认为 ECC 将会取代 RSA 算法。

但这并不意味着 RSA 算法在现在就已经过时了。RSA 算法更加久经考验，适用范围和兼容性更好。满足当前安全强度所需的密钥长度还在可接受范围内，只是性能差了点。

密钥强度

密钥强度是指暴力破解所需的计算复杂度，通常用位来表示。

对于对称加密算法来说，密钥强度比较直接。例如 AES-128 算法的密钥强度就是 128 位。因为对称加密算法暴力破解的方式就是把所有的密钥可能都试一遍，没有更好的方法了。

而非对称加密算法暴力破解则可以根据一些数学特性有更高效的破解方法，所以密钥强度并不等同于其密钥长度。例如 3072 位的 RSA 算法和 256 多位的椭圆曲线算法都大概只有 128 位的密钥强度。也就是说要破解 3072 位的 RSA 算法，并不需要计算 2^3072 次，只需要计算 2^128 次就够了。

具体密钥强度的对应关系，以及不同算法推荐使用的密钥长度可以参考 Keylength - NIST Report on Cryptographic Key Length and Cryptoperiod (2020)。