根据博迪投资学第九版课后习题完成的系列。每道题都有完整的步骤,附上推理过程和错误答案批驳,以辅助理解。市面上的笔记和视频都太乱,希望这份笔记能以数理严谨性帮到大家。
中英文习题都是一样的,部分数据中文版教材有修改,笔记会注明。供学习博迪投资学,以及备考金融硕士431的同学参考。欢迎老师、同学指正!
格式说明:黑色为正文,含答案和步骤。橙色带双斜//的是注释,学过C++的都非常熟悉。灰色带删除线的代表我自己一刷的时候的错误答案及错因解读,供参考。
基础题
1E
//易错点提示:给定A,确实可以求出IC曲线。但已知条件没说U必须是固定的。
整个单元提到的组合,就是无风险资产和风险资产的组合。CAL上的夏普比例不变。
由A的基础定义,A较高的时候,投资者不会选择风险更高的组合,也就是对P点,只会选择第二象限组合,对应不同的U。
厌恶风险的时候,RP会更高,但不代表投资者会对此有偏好。
//以下为错误答案AD
由定义,U=E(rp) -1/2 *A * σ^2
A较高时,y低,不会投资过多风险资产。排除B。
风险溢价为E(rp) -rf,U一定,rf为常数。A↑必然有E(rp) ↑,从而RP也↑,A选项正确。
夏普比例为(E(rp) -rf)/σ。对同一σ,A越高的人,会要求更高Erp,D正确。
2B
对A,CAL上的y与SR函数无关。排除。
对B,SR是CAL的斜率。y>1时,若RB借贷利率高于rf,SR分子溢价降低,曲线斜率降低。正确。
对C,由于无风险利率不变,[2E(r )-rf]/2σ高于2SR,不是简单翻倍关系。排除。
对D,RP不变,但分母的σ会由于Er提高而增大,SR降低。排除。
3y*会下降
//题目有误,应当问的是配置到风险资产的头寸比例y*,才对应方程6.7.
中等题
4
1)期望现金流E(CF)=0.5*70000+0.5*200000=135000
必要报酬率k=8%+6%=14%
对应筹资PV=E(CF)/(1+k)=135000/1.14=118421.05
//实质是公司理财估值,数学上就是求现值的运算
2)初始投资118421.05元,期末收入135000元,对应投资回报率为
E(R )=135000/118421.05-1=14%,与考虑风险溢价后的必要报酬率一致
必要报酬率k=8%+6%=14%
//公司或项目估值,用的资本成本是必要报酬率。对投资人,是已经知道价格,反求出来的收益率、利率,是期望报酬率。
3)必要报酬率k=12%+6%=18%
对应现值P=E(CF)/(1+k)=135000/1.18=114406.78
必要报酬率k=12%+6%=18%
//问你现在愿意出多少钱,等同于问给定报酬率下,公司能筹多少资本。
//投资人愿意出的钱变少了,是因为风险变高,必要报酬率增大。增加的就是对公司经营风险的惩罚。
//疑问:先出现金流,还是先出收益率?
//答:取决于目前任务是估值,还是求收益率。分别对应公司理财和投资学。
5
无风险资产效用U(f)=rf=0.07
风险资产效用U(p)=0.12-0.5*A*0.18^2
当风险资产相对无风险资产更有吸引力时,必有:0.12-0.5*A*0.18^2≥0.07
A≤0.05/(0.5*0.18*0.18)=3.09
最大风险厌恶系数为3.09
//以效用决策,偏好风险资产,未必代表只投资风险资产,而是U(p)>U(f).
//不要把问题复杂化,变成考虑CAL约束和rf被消掉的问题。因为这时候反而增加了标准差和头寸y等自变量,不等式更难解。
//易错点提示:不是所有决策都要用到y*。
有两种决策依据。
以效用决策,需要根据A和U定IC,上面的点随便选。
以CAL决策,根据偏好选上面的点,未必是最优头寸y*。
如果是用无风险资产和风险资产进行组合,就必须选出一个y,使得CAL和IC有交点。
这个点就是风险资产最优头寸点y*。
错误答案:
设风险资产最优头寸y*=(E(rp) -rf)/A*σ^2
仍然偏好风险资产的情况下,y*>0.
A*σ^2=(E(rp) -rf)/y*,则A=(E(rp) -rf)/(y**σ^2)=0.05/0.0324y*=
//疑问:这个题要解不等式吗?
//答:肯定要解不等式,关键是概念理解。
6-7
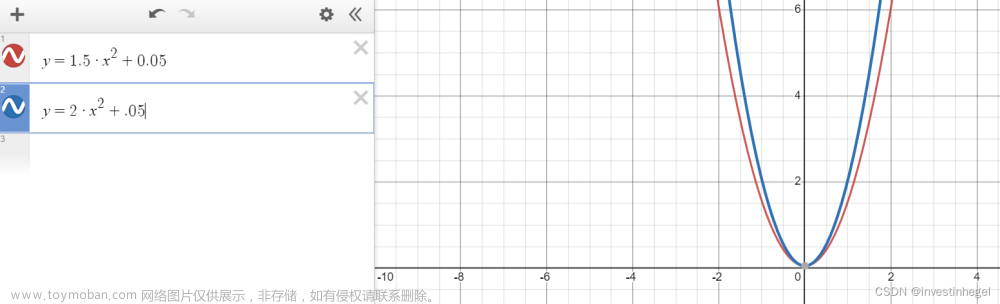
0.05=E(rp)-1.5σ^2
为二次函数。
风险系数改为A=4,曲线更陡。
8-9
风险中性投资者的A=0,IC为0.05=E(rp),是一条直线
风险喜好投资者的A<0
0.05=E(rp)-0.5*(-4)*σ^2
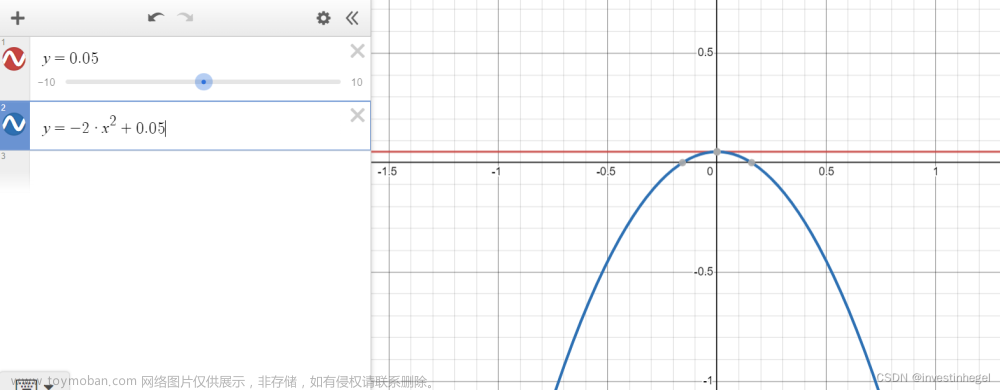
//疑问:抛物线向下的时候,符合人性吗?数学上可以定义吗?
//答:确有其事。在3D二元函数中,负A使∂U/∂σ为正,代表波动率越高,U或者确定等价收益率越高。
梯度向量是函数降一个维度后,等值面/线的法向量。显然,西北、正北和东北,分别代表了U作为二元函数时,由于A的不同,所取得的不同梯度向量箭头位置。
10-12
10.公式为E(rc)=y*E(rp)+(1-y)*rf=0.05+0.03*y
Var(rc)=y^2 * σ(p)^2=0.04*y^2
效用水平为U=0.05+0.03*y-0.5*A*0.04*y^2=0.05+0.03*y-0.02*A*y^2
//提示:效用再列y的公式就太慢了,不如用定义和已有结果算。
效用水平为U=E(rc)-0.5*A*Var(rc)
A=2,U=E(rc)-Var(rc)
A=3,U=E(rc)-1.5*Var(rc)
六种投资组合的期望收益和方差如下
| 组合风险头寸y |
组合期望收益 |
组合方差 |
A=2的效用 |
A=3的效用 |
| 1 |
0.08 |
0.0400 |
0.0400 |
0.02 |
| 0.8 |
0.074 |
0.0256 |
0.0484 |
0.0356 |
| 0.6 |
0.068 |
0.0144 |
0.0536 |
0.0464 |
| 0.4 |
0.062 |
0.0064 |
0.0556 |
0.0524 |
| 0.2 |
0.056 |
0.0016 |
0.0544 |
0.0536 |
| 0 |
0.05 |
0.0000 |
0.0500 |
0.05 |
//提示:网上提供的英文标答是第七版的,风险回报率13%,所以算出来全都不一样。我以第九版习题为准。
//用python解矩阵、表格题,还不如excel快
13-19
13.y=0.7时,
E(rc)=0.08+0.7(0.18-0.08)=0.15
Var(c )=(0.7*0.28)^2=0.0384
14.客户的头寸为:
| 股票A |
17.5% |
| 股票B |
22.4% |
| 股票C |
30.1% |
| 短期国债 |
30% |
15.根据夏普比例定义,
我管理的风险组合的报酬——波动性比率为(E(rp)-rf)/σp=(0.18-0.08)/0.28=0.3571
客户的报酬——波动性比率为(0.15-0.08)/(0.7*0.28)=0.3571
说明在CAL线上的夏普比例,与风险头寸无关。
16.资本配置线斜率为SR=0.3571

17.由E(rc)相对于y的函数表达式,
0.16=0.08+y*0.1
解得y=0.8
此时客户组合的收益标准差=0.8*0.28=0.224
18.由E(rc)相对于σc的表达式,
E(rc)=rf + σc * SR=0.08+0.3571*σc
取最大组合标准差,得最大组合收益率0.1443
由E(rc)相对于y的表达式,
0.1443=0.08+y*0.1
解得y=0.643
即:客户需要将64.3%的资金配置到我管理的风险组合里
//疑问:如何将标准差和期望收益联系?E(rc)有哪些形式?
//答:E(rc)关于y的表达式,源于期望运算定义;
E(rc)关于σc的表达式,源于均值——标准差坐标系下的点斜式方程
已知A,则可以求出y*头寸,从而求出E(rc)。
此外,第五章还有对数正态分布下的算法
19.当A=3.5时,客户组合的效用为U=E(rc)-0.5*3.5*σc^2
E(rc)=0.08+y*0.1
σc^2=0.0784*y^2
代入得U(y)=0.08+y*0.1-0.1372y^2
令d U/dy=0.1-0.2744y=0,解得y=0.3644 //注意别把常数项抄错成一次项
观察二阶导数d 2U/dy2 =-0.2744<0,
由极值第二充分条件,可知y=0.3644为最大值点。
因此,应当建议客户把36.44%的资金投入我管理的风险组合,剩余资金购买短期国债。
//提示:CAL与IC的均衡是资本市场默认条件,所以已知A和大盘数据,可以直接求y*,不用每次都证明这个公式
20
大盘数据如下:

1)若A=4,设投资y到股票,由IC和CAL公切点性质得:
y*=RP/A*σ^2=7.93%/4*20.81%^2=0.4578
所以,应配置45.78%的资金到股市,54.22%的资金到短期国债。
2)同上,代入60-80年代的数据,得
y*=3.44%/(4*16.71%^2)=0.3080
所以,应配置30.80%的资金到股市,69.20%到短期国债。
3)方案二的风险溢价相对于标准差,比方案一低更多,因此y*更低。
风险资产最优头寸,实际上取决于投资者的风险厌恶程度和对历史数据的判断。
选用60-80年代的数据,表明方案二的风险厌恶程度更高。
21
1)设风险组合头寸为y
由E(rc)关于y的函数表达式得
0.08=0.05+y*(0.11-0.05)
解得y=0.5
故客户应当把50%的资金投入到我的风险组合里。
2)组合标准差为σc=0.5*0.15=0.075
3)由CAL的定义和性质,可推出一阶常系数线性方程组:
E(rc)=rf+y*RP
E(rc)=rf+σc*RP/σp
显然,y*RP=σc*RP/σp
解得y=σc/σp,是关于σc的单调递增函数
由于E(rc)也是关于y的单调递增函数,
显然取最大标准差时,可得最大收益。
此时y=0.12/0.15=0.8
E(rc)=0.05+0.8*0.06=0.098
22
使用资本市场线提供投资建议时,风险组合为市场组合,资本配置线就是资本市场线。
由资本配置线性质,E(rc)=rf+σc*(E(rc)-rf)/σp
即E(rc)=0.05+0.07*σc/σp①
根据客户需求,σc=0.5*σp②
联立解得E(rc)=0.085
由标准差的线性性质,设配置到市场组合的头寸比例为y,则有σc=y*σp
显然y=0.5
所以,约翰逊若将50%的资金投资IMI的市场组合,50%投资于无风险资产,可得目标期望收益率8.5%
23.
标普500指数:E(rp)=0.13,σp=0.25,rf=0.05
无杠杆时,CML对应SRm=(0.13-0.05)/0.25=0.32
由点斜式解得CML方程:E(rc)=0.32σc+0.05
发生借款时,SRb=(0.13-0.09)/0.25=0.16
不可导点对应y=1,则σc=σp=0.25,E(rc)=0.13
由点斜式解得E(rc)=0.13+0.16(σc-0.25)=0.16σc+0.09
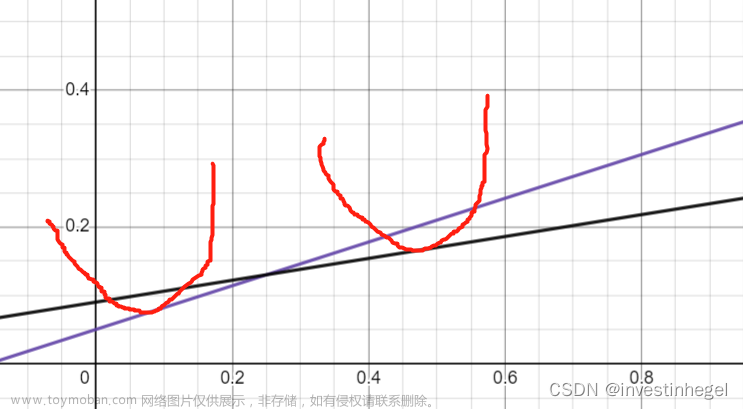
//注意:由概率论定义,标准差非负;
由货币银行学,名义利率非负;
因此笛卡尔坐标系只有第一象限,在投资学的讨论中有意义。
24.分类讨论组合配置y
若y<1,则每个切点都满足0.08/A*0.0625<1,解得A>1.28
若y>1,则每个切点都满足0.04/A*0.0625>1,解得A<0.64
当y=1时,切点的A处于上述两个区间并集的补集:
0.64≤A≤1.28
//首先:不考虑分段函数问题,正常的CAL曲线从未规定任何A或者U,也没说只能有一个切点。
//第二:CAL上选择的每个组合(E(rc), σc),都一定是与某条IC的切点。如果是普通交点,投资者一定会追求更高U,从而沿梯度向量方向选择更高IC,最终会使得(E(rc), σc)成为IC与CAL唯一交点。
//标答解法用的是德摩根定律。定义事件M=y=1,则非M=y<1或y>1,二者为互斥补集。
//疑问:为什么24题可以求出一个范围?在CAL分两段的情况下,切点问题如何理解?
//答:A本身也是可变量,从而使得切点在CAL上不断变化。分两段的时候,必然A是可以解出区间的。
25
我管理的基金:E(rp)=0.11,σp=0.15,rf=0.05
无杠杆时,CAL对应SRp=(0.11-0.05)/0.15=0.4
由点斜式解得CAL左半段方程:E(rc)=0.4σc+0.05
发生借款时,SRb=(0.11-0.09)/0.15=0.1333
不可导点对应y=1,则σc=σp=0.15,E(rc)=0.11
由点斜式解得CAL右半段方程:E(rc)=0.11+0.13(σc-0.15)=0.13σc+0.0905
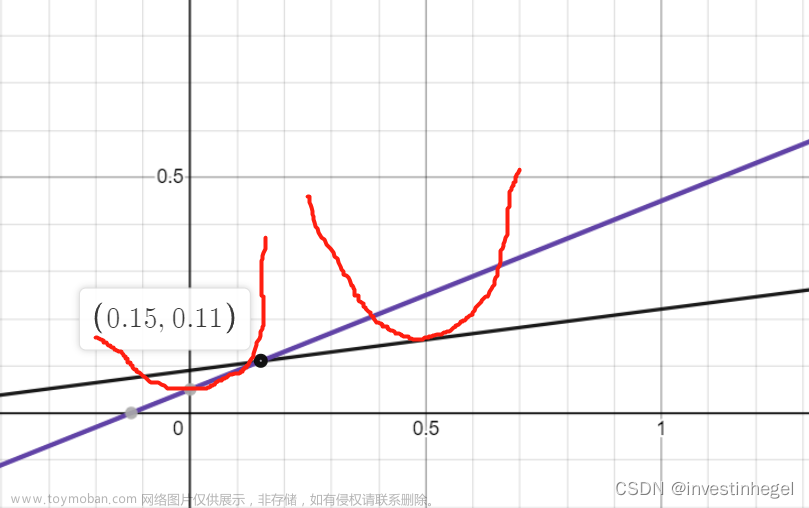
当投资者贷出资金时,y<1,即0.06/A*0.0225<1,解得A>2.67
当投资者借入资金时,y>1,即0.02/A*0.0225>1,解得A<0.89
当y=1时,投资者将自有资金全部投入我管理的基金。
由德摩根定律,此时A的取值是上述两段并集的补集:
0.89≤A≤2.67
26.由题意,基金管理费是投资成本之一,应当从投资收益中扣除。
由理性经济人假设,投资人选择我管理的基金,必然是因为费后收益更高,且风险可控。
用报酬——波动性比率衡量我的基金和大盘表现。
在y<1时,得不等式:
(0.11-0.05-f)/0.15 ≥ (0.13-0.05)/0.25
解得f≤0.012
在y>1时,得不等式:
(0.11-0.09-f)/0.15≥(0.13-0.09)/0.25
解得f≤-0.004
意味着我作为基金管理者,需要向投资人倒贴费用,才能吸引他们投入我的组合中。
综上所述,贷出资金的投资者不会愿意支付管理费,会采用被动投资策略。
借入资金的投资者最多愿意支付1.2%的管理费。
//疑问:基金管理费是什么GUI?教材哪说了这个?
//答:费用和收入问题,可以用公司理财的思维解决。
高级题
27.
被动策略E(r )=0.13,σ=0.25
主动策略E(r )=0.18,σ=0.28
无风险利率rf=0.08
CAL斜率=(0.18-0.08)/0.28=0.3571
CML斜率=(0.13-0.08)/0.25=0.2
我的组合较被动组合的优势,是斜率更高,夏普比例更高。即,在同样的风险条件下,我的组合能提供的风险溢价,以及期望收益更高。
28.
1)//故事:全部都是服务客户。一开始100元,70元买我的基金,30元买国债;现在想不动国债,把70元基金赎回去,买沪深300指数基金。对开放式基金而言,我的AUM会受到影响。
公司金融,决策用NPV法或IRR法,综合项目现金流入流出情况和公司资本成本,实际就是在业财二维下考虑收益和成本。
投资学,决策不考虑折现,只看(E(rc),σ),实际也是本量利模型的扩展。
提醒注意表达规范性。被动组合是市场组合,因此CAL会变成CML,公式的p要换成m
//以下为答案:
被动策略E(r )=0.13,σ=0.25
主动策略E(r )=0.18,σ=0.28
无风险利率rf=0.08
显然,这是个互斥方案的优选问题:
对客户而言,如果选择我管理的主动基金,按y=70%配置下来,组合表现为:
E(rc)=rf+y*[E(rp)-rf]=0.08+0.7*0.1=0.15
σc=y*σp=0.7*0.28=0.196
如果选择投资指数基金,组合表现为:
E(rc)=rf+y*[E(rm)-rf]=0.08+0.7*0.05=0.115
σc=y*σm=0.7*0.25=0.175
若客户选择转移资金,收益会下降,但标准差也会下降。因此,要用其他指标对客户的选择做评估。以下证明:若客户愿意接受较低的11.5%的收益率,把资金投入到我管理的主动基金,仍然是更好的选择。
由资本配置线方程,如果客户期望收益率为11.5%,有另一种配资选择:
0.115=0.08+y*0.1
解得y=0.35,意味着就收益率而言,以下两种方案,对客户等价:
方案三:将35%的资金投入到我的基金,剩余65%全部买短期国债
方案二:70%资金投入指数基金,30%资金购买短期国债
方案三对应的标准差为σc=0.35*0.28=0.098,远低于方案二。
因此,若客户风险厌恶系数较高,建议选择方案二;若风险厌恶系数较低,建议维持原方案。
无论如何,撤资对客户都不是最好的选择。
//附初始答案,显然是没有把公司金融和投资学打通。
资本市场线的斜率低于资本配置线,意味着风险相同的情况下,客户能获得的收益变低。此外,转换还会带来交易成本
2)如果要获得与被动策略等效用,
(0.18-0.08-f)/0.28=(0.13-0.08)/0.25
解得f=0.044
最高管理费用为4.4%
//题目没给出系数A,所以只能用SR代替U衡量效用
29
我管理的风险组合满足:E(r )=0.18,σ=0.28,rf=0.08
该客户的风险厌恶系数A=3.5
1)在被动组合中,y=(0.13-0.08)/(3.5*0.25^2)=0.2286
2)要使得客户投资于我的组合和被动组合没有差异,我能征收的最高管理费用f满足以下条件:
(0.18-0.08-f)/0.28=(0.13-0.08)/0.25
最高管理费用为4.4%
CFA考题
1-3
| U=E(rp)-2*Var |
U=E(rp) |
|||
| 投资 |
期望收益 |
标准差 |
A=4效用 |
A=0效用 |
| 1 |
0.12 |
0.3 |
-0.06 |
0.12 |
| 2 |
0.15 |
0.5 |
-0.35 |
0.15 |
| 3 |
0.21 |
0.16 |
0.1588 |
0.21 |
| 4 |
0.24 |
0.21 |
0.1518 |
0.24 |
作为风险厌恶系数4的投资者,会选择效用最高的组合3.
作为风险中性的投资者,会选择期望收益最高的组合4.
由定义,A是风险厌恶系数,代表一个单位的收益率与0.5个方差交换的比例,故选B
4-5

IC必与CAL相交或相切,投资者可达到的最大效用对应2号IC。
最佳风险投资组合,对应切点F。
6
E(R )=0.6*50000+0.4*(-30000)=18000
RP=18000-5000=13000
7
资本配置线在Y=1处不可导,是因为右侧投资者借款利率必然高于无风险利率,SR的RP必然下降。
选B
8-9//这道题中文翻译版篡改了英文原题,以英文版数据为准
由E(rc)相对于y的函数表达式,客户组合特征为
E(rc)=0.06+0.6*0.1=0.12
σc=0.6*0.14=0.084
我管理的基金SR=0.1/0.14=0.7143
//以下为计算错误的答案
由E(rc)相对于y的函数表达式,客户组合特征为
E(rc)=0.06+0.6*0.1=0.66 //易错点:0.6*0.1≠0.6,注意小数点后移两位
σc=0.6*0.14=0.084文章来源:https://www.toymoban.com/news/detail-500122.html
SR=0.1/0.084=1.19 //错因:分子用基金的数据,分母用客户的数据文章来源地址https://www.toymoban.com/news/detail-500122.html
到了这里,关于投资学U06 风险资产配置 习题笔记的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!