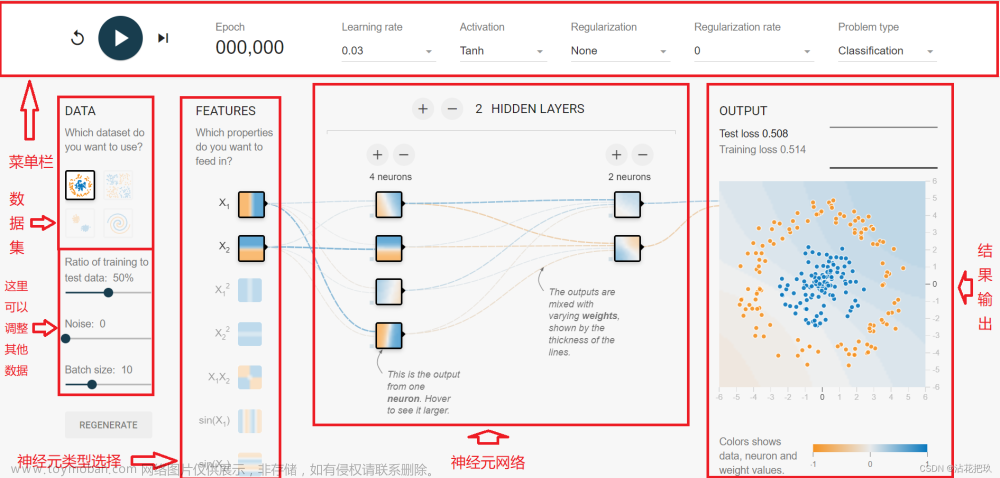
【神经网络的构成】
神经元 激活函数 层
feedforward computation前向计算:从输入开始依次计算每一层的结果。
隐层:在输入之上添加的多层通常被称为隐层。
激活函数:非线性的激活函数,拟合非线性关系,进行非线性变换。
叠加若干隐层,提升网络的表达能力。
输出层:来得到结果。线性输出层,用来解决回归问题。sigmoid输出层,将结果压到0-1之内,用来解决二分类问题。softmax输出层,用来解决多分类问题。
【如何训练】
目标:均方差越小,模型越好。Mean Squared Error。每个预测值和真实值差的平方和再求平均。将均方差定义为损失函数,也就是所谓的loss。训练的目标就是去减小这个损失函数的值。
如果是分类任务呢,目标就是最小化交叉熵Cross-entropy.
如何使损失函数最小化,采用梯度下降法,把整个优化过程拆分成一个个步骤,每一步,缩小损失函数一点点。如何调整参数,才能使损失函数逐步变小呢。这需要去求损失函数对于模型参数的梯度,梯度代表了对这个参数进行单位大小的改动,然后损失函数它变化最快的方向。我们就顺着这个方向去对模型参数做一个小的改动,就可以降低一点点损失函数。因为我们目标是使损失函数最小,所以我们要做沿着梯度的反方向去改动/走一小步。
改动/步幅的大小取决于“学习率”。
反向传播:把上游神经元层的梯度,传递到下游神经元层的梯度,从上游到下游逐层计算每层参数要进行的小变动。文章来源:https://www.toymoban.com/news/detail-500634.html
随机梯度下降:以上计算梯度下降时用的是全部样本&文章来源地址https://www.toymoban.com/news/detail-500634.html
到了这里,关于大模型基础之神经网络的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!