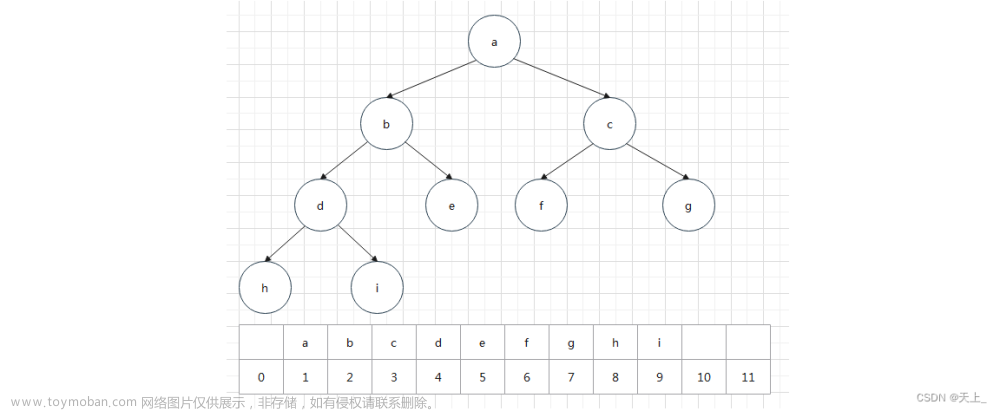
图是描述复杂事务的数据表示形式，由节点和边组成，数学上一般表述为G（V，E）。其中的V（vertical）代表节点，可被理解为事物；E（edge）代表边，描述的是两个事物之间的关系。例如一个图的社交网络图，每个人都可视为节点，而人与人之间的关系可被视为边。
节点的邻居（neighbor）指的是与该节点在同一边另一端的节点。节点的度（degree）指的是该节点邻居的数量.
1、图的分类：
（1）按边有无方向，可将图分为有向图和无向图，如下图所示。有向边的出发节点称为头节点，结束节点则称为尾节点。
（2）按节点和边的类别数量，可将图分为同构图和异构图。下图左边的图只有一类节点（用户）和一类关系（朋友关系），即为同构图。若节点类别数量大于1，或关系类别数量大于1，如下图右边所示，则该图为异构图。
（3）按边是否带有权重可分为无权图和有权图。
2、图的表示：
指计算机以何种方式表示图。
（1）邻接矩阵。假设一个图的节点数量为N，则生成一个N*N的矩阵。矩阵中的值为对应位置节点与节点之间的关系，一般用A表示。
一个图中，若节点X与节点Y有边连接，则在邻接矩阵的对应位置赋值1即可，若两节点间无边连接则赋值0。无向图的邻接矩降是一个以对角矩阵镜像对称的矩阵。而有向图中，将邻接矩阵的行索引代表有向图中有向边的头节点，列索引代表尾节点，则有向图的邻接矩阵不再是对称矩阵。
若图中有多种关系即异构图，则需要多个邻接矩阵，每种关系对应一个邻接矩阵。
若图带有权重，则邻接矩阵中不再是0和1，而是对应的权重值。
缺点：随着图中节点或关系数量的增长，会使邻接矩阵的维度或个数快速增长，变得异常稀疏。
（2）邻接列表。邻接列表为图中每一个头节点生成一个list，如节点2有一条通向节点1的边和一条通向节点3的边，那么可表示为2 : [ 1 , 3 ]。若边分别带有权值0.5和0.6，可表示为2 : [ (1,0.5) , (3,0.6) ]。
（3）边集。以头尾节点的索引元组表示一条边。例如头节点是h，尾节点是t，那么这一条有向边就是（h, t），如果是一条无向边则就用一对对称元组表示，即（h, t）, (t, h)。
3、知识图谱：
知识图谱是一种高度结构化的数据形式，可以看作是一个有向异构图。一般以三元组的形式存储，对于头节点h、尾结点t以及它们之间的关系r，以三元组（h,r,t）表示。文章来源：https://www.toymoban.com/news/detail-501032.html
文章来源地址https://www.toymoban.com/news/detail-501032.html
到了这里，关于图的分类及表示方式的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
