蒙特卡洛算法
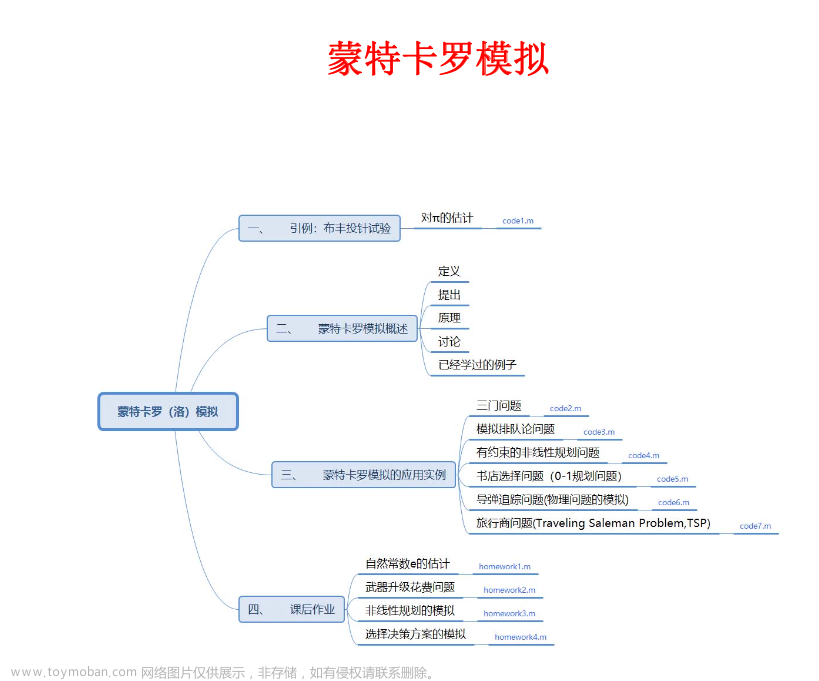
定义:蒙特卡洛算法是以概率和统计的理论、方法为基础的一种数值计算方法,将所求解的问题同一定的概率模型相联系,用计算机实现统计模拟或抽样,以获得问题的近似解,故又称随机抽样法或统计实验法。
适用范围:可以较好的解决多重积分计算、微分方程求解、积分方程求解、特征值计算和非线性方程组求解等高难度和复杂的数学计算问题。
特点:蒙特卡洛算法可以应用在很多场合,但求的是近似解,在模拟样本越大的情况下,越接近于真实值,单样本数增加会带来计算量的大幅上升。对于一些简单问题来说,蒙特卡洛是个笨办法,但对于许多问题来说,它往往是个有效,有时甚至是唯一可行的方法。matlab代码
%作图的代码
x = 0:0.25:12;
y1 = x.^2;
y2 = 12 - x;
plot(x, y1, x, y2)
xlabel('x');ylabel('y');
%产生图例
legend('y1=x^2', 'y2=12-x');
title('绘制');
%图中x轴和y轴的范围,中括号前面是y轴范围,中括号后面是x轴范围
axis([0 15 0 15]);
text(3, 9, '交点');
%画图时加上网格线
grid on
%蒙特卡洛算法的具体实现
%产生一个1行10000000列的矩阵,矩阵中每个数是从0到12之间随机取
x = unifrnd(0, 12, [1, 10000000]);
y = unifrnd(0, 9, [1, 10000000]);
frequency = sum(y<x.^2&x<=3)+ sum(y<12-x&x>=3);
area = 12*9*frequency/10^7;
disp(area);

数据拟合
定义:不要求近似函数通过所有的数据点,而是要求他能较好的反应数据的整体变化趋势。
常用方法:最小二乘拟合方法matlab代码
%读取表格
A = xlsread('D:\表格\1.xls', 'Sheet1', 'A1:AN2');
B = A;
[I, J] = size(B);
%数据拟合
%x为矩阵的第一行,y为矩阵的第二行
x = A(1,:);
y = A(2,:);
%polyfit为matlab中的拟合函数,第一个参数是数据的横坐标
%第二个参数是数据的纵坐标,第三个参数是多项式的最高阶数
%返回值p中包含n+1个多项式系数
p = polyfit(x, y, 2);
disp(p);
%下面是作图的代码
x1 = 300:10:600;
%polyval是matlab中的求值函数,求x1对应的函数值y1
y1 = polyval(p,x1);
plot(x,y,'*r',x1,y1,'-b');
%plot(x,'DisplayName','x','YDataSource','x');
%figure(gcf);
插值
定义:在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。
作用:插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值情况,估算出函数在其他点处的近似值。
区别:从定义上看,插值和拟合有一定的相似度,但插值要求近似函数通过给定的所有离散数据,而拟合并不要求这样,只要近似函数能较好的反映数据变化的趋势即可(近似含义不同),当测量值是准确的,没有误差时,一般用插值;当测量值与真实值有误差时,一般用数据拟合。matlab代码
%years、service和wage是原始数据
years = 1950:10:1990;
service = 10:10:30;
wage = [ 150.697 199.592 187.625 179.323 195.072; 250.287 203.212 179.092 322.767 226.505;153.706 426.730 249.633 120.281 598.243];
[X, Y] = meshgrid(years, service);
% % 三维曲线
% plot3(X, Y, wage)
% 三维曲面
figure
surf(X, Y, wage)
%interp2是matlab中的二维插值函数,前两个参数是已知未知,后两个是未知位置,w是未知位置的插值结果
w = interp2(service,years,wage,15,1975);

线性规划
定义:线性规划是研究线性约束条件下线性目标函数的极值问题的数学理论和方法。
步骤:
(1)根据影响所要达到目的的因素找到决策变量。
(2)由决策变量和所在达到目的之间的函数关系确定目标函数。
(3)由决策变量所受的限制条件确定决策变量所要满足的约束条件。
特点:目标函数是决策变量的线性函数。根据具体问题可以是最大化或最小化,二者统称为最优化。约束条件也是决策变量的线性函数。Lingo代码
model:
min = 2*x1 + 3*x2;
x1 + x2 >= 350;
x1 >= 100;
2*x1 + x2 <= 600;
end
整数规划
定义:整数规划是指规划中的变量(全部或部分)限制为整数,若在线性模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法往往只适用于整数线性规划。
分类:在整数规划中,如果所有变量都限制为整数,则称为纯整数规划;如果仅一部分限制为整数,则称为混合整数规划。整数规划的一种特殊情形是0-1规划,它的变数仅限于0或1。
0-1规z划:问题中许多量具有不可分割的性质(最优调度的车辆数、设置的销售网点数…),或者问题的解必须满足一些特殊的约束条件(满足逻辑条件、顺序…),需引入逻辑变量(0-1变量)以表示“是”与“非”。这类问题的模型均为整数规划。
Lingo实现整数规划(一般的整数规划)
model:
min = 2*x1 + 3*x2;
x1 + x2 >= 350;
x1 >= 100;
2*x1 + x2 <= 600;
!@gin(变量)表示该变量只能取整数;
@gin(x1);
@gin(x2);
end
灰色预测法
优点:所需建模信息少、运算方便、建模精度高,适应于小样本预测问题。matlab代码:文章来源:https://www.toymoban.com/news/detail-501207.html
%%构建GM模型计算出a和b
%建立符号变量a(发展系数)和b(灰作用量)
syms a b;
u = [a b]';
%原始数列X0
X0 = input('请输入数据');
n = length(X0);
%对原始数列X做累加得到数列X1
X1 = cumsum(X0);
%对数列X1做等权邻值生成Z1
for i = 2: n
Z1(i) = (X1(i) + X1(i - 1)) / 2;
end
Z1(1) = []; %去除掉第一个元素
%构造数据矩阵
B = [-Z1; ones(1, n - 1)]';
Y = [X0]';
Y(1, :) = []; %去除掉第一个元素
%利用u = inv(B'*B)*B'*Y来求解
u = inv(B'*B) * B' * Y;
a = u(1, :);
b = u(2, :);
%%预测后续数据
%p是预测后续的数据量,根据情况可更改
p = 3;
%构建预测数列F
F = []; F(1) = X0(1);
for i = 2: (n + p)
F(i) = (X0(1) - b/a) * exp(-a*(i-1)) + b/a;
end
%对数列F累减还原,得到预测出的数据
G = []; G(1) = X0(1);
for i = 2: (n + p)
G(i) = F(i) - F(i-1);
end
disp('预测到的数据为:');
G
%%模型检验
H = G(1: n);
%计算残差序列
E = X0 - H;
%法一:相对残差Q检验
%计算相对误差序列
epsilon = abs(E ./ X0);
%计算相对误差Q
disp('相对残差Q检验:');
Q = mean(epsilon)
%法二:方差比C检验
disp('方差比C检验:');
C = std(E, 1) / std(X0, 1)
%小误差概率P检验
S1 = std(X0, 1);
tmp = find(abs(E - mean(E)) < 0.6745 * S1);
disp('小误差概率P检验:');
P = length(tmp) / n
模拟退火算法
优点:模拟退火算法是一个解决最优化问题的算法。文章来源地址https://www.toymoban.com/news/detail-501207.html
matlab实现
clc,clear %清空环境中的变量
tic
iter = 1; % 迭代次数初值
a=0.99; %温度衰减系数
t0=120; %初始温度
tf=1; %最后温度
t=t0;
Markov=10000; %Markov链长度
load data1.txt %读入城市的坐标
city=data1;
n = size(city,1); %城市距离初始化
D = zeros(n,n);
for i = 1:n
for j = 1:n
D(i,j) = sqrt(sum((city(i,:) - city(j,:)).^2));
end
end
route=1:n;
route_new=route;
best_length=Inf;
Length=Inf;
best_route=route;
%%
while t>=tf
for j=1:Markov
%进行扰动,长生新的序列route_new;
if (rand<0.7)
%交换两个数的顺序
ind1=0;ind2=0;
while(ind1==ind2&&ind1>=ind2)
ind1=ceil(rand*n);
ind2=ceil(rand*n);
end
temp=route_new(ind1);
route_new(ind1)=route_new(ind2);
route_new(ind2)=temp;
else
ind=zeros(3,1);
L_ind=length(unique(ind));
while (L_ind<3)
ind=ceil([rand*n rand*n rand*n]);
L_ind=length(unique(ind));
end
ind0=sort(ind);
a1=ind0(1);b1=ind0(2);c1=ind0(3);
route0=route_new;
route0(a1:a1+c1-b1-1)=route_new(b1+1:c1);
route0(a1+c1-b1:c1)=route_new(a1:b1);
route_new=route0;
end
%计算路径的距离,Length_new
length_new = 0;
Route=[route_new route_new(1)];
for j = 1:n
length_new = length_new+ D(Route(j),Route(j + 1));
end
if length_new<Length
Length=length_new;
route=route_new;
%对最优路线和距离更新
if length_new<best_length
iter = iter + 1;
best_length=length_new;
best_route=route_new;
end
else
if rand<exp(-(length_new-Length)/t)
route=route_new;
Length=length_new;
end
end
route_new=route;
end
t=t*a;
end
%--------------------------------------------------------------------------
%% 结果显示
toc
Route=[best_route best_route(1)];
plot([city(Route ,1)], [city(Route ,2)],'o-');
disp('最优解为:')
disp(best_route)
disp('最短距离:')
disp(best_length)
disp('最优解迭代次数:')
disp(iter)
for i = 1:n
%对每个城市进行标号
text(city(i,1),city(i,2),[' ' num2str(i)]);
end
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['模拟退火算法(最短距离):' num2str(best_length) ''])
到了这里,关于蒙特卡洛算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!