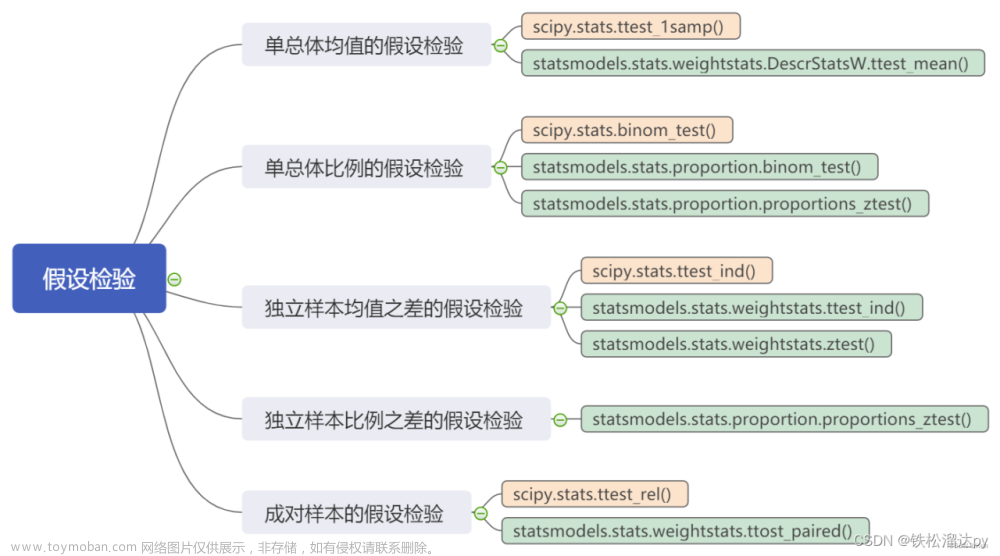
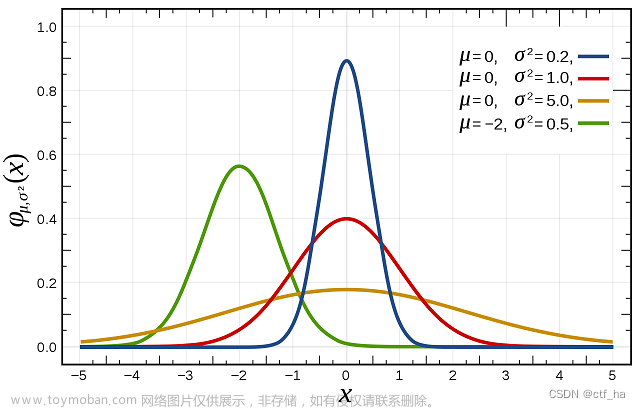
一、假设检验的基本思想
假设检验的思想和方法是根据小概率原理，具体地说当我们对问题提出原假设H0和备注假设H1，并要检验H0是否可信时，可以先假设H0是正确的，在此假设下，经过一次抽样，若发生小概率事件，可以根据“小概率事件在一次实验中几乎是不可能发生的”的理由，怀疑原假设不真，从而拒绝原假设H0,反之，如果小概率事件没有发生，就没有理由拒绝H0，从而接受H0。
总而言之，假设检验是指先对总体的参数提出某种假设，然后利用样本的信息判断假设是否成立的过程。比如醉驾判定为刑事犯罪后是否会使得交通事故减少、男生和女生在选文理科时是否存在性别因素影响。
二、假设检验的步骤
- 提出假设: 原(零)假设H0与备择假设H1
- 确定适当的检验统计量
- 规定显著性水平 α \alpha α
- 计算检验统计量的值
- 做出统计决策：检验统计量的值与显著性水平的临界值进行比较，得出拒绝或不拒绝原假设的结论
三、左侧检验、右侧检验、双侧检验
单侧检验指按分布的一侧计算显著性水平概率的检验。用于检验大于、小于、高于、低于、优于、劣于等有确定性大小关系的假设检验问题。这类问题的确定是有一定的理论依据的。假设检验写作：μ1<μ2或μ1>μ2。 。
- 左侧检验：当关键词有不得少于/低于的时候用左侧。
-
右侧检验：当关键词有不得多于/高于的时候用右侧，比如次品率不得多于/高于5%时。
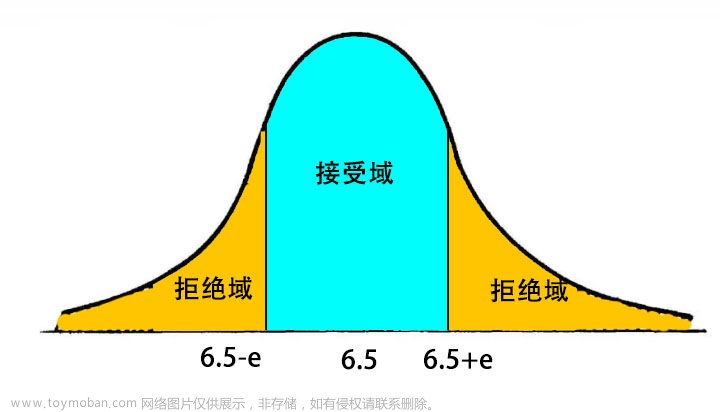
- 双侧检验：双侧检验指按分布两端计算显著性水平概率的检验， 应用于理论上不能确定两个总体一个一定比另一个大或小的假设检验。一般假设检验H1：μ1≠μ2。若p值>
α
/
2
\alpha/2
α/2,接受原假设，p值<
α
/
2
\alpha/2
α/2，则拒绝原假设
四、参数检验与非参数检验的区别
- 1、定义不同
参数假设检验（parameter test）：假定数据服从某分布（一般为正态分布），通过样本参数的估计量（x±s）对总体参数（μ）进行检验，比如t检验、u（z）检验、方差分析。
非参数检验(Nonparametric tests)：不需要假定总体分布形式，直接对数据的分布进行检验。由于不涉及总体分布的参数，故名「非参数」检验。主要方法包括卡方检验、二项分布检验、K-S检验以及变量值随机性检验等方法。
-
2、参数检验的集中趋势的衡量为均值，而非参数检验为中位数。
-
3、参数检验需要关于总体分布的信息；非参数检验不需要关于总体的信息。
-
4、参数检验只适用于变量，而非参数检验同时适用于变量和属性。
-
5、参数检验是针对参数做的假设；非参数检验是针对总体分布情况做的假设文章来源：https://www.toymoban.com/news/detail-501659.html
-
文章来源地址https://www.toymoban.com/news/detail-501659.html
到了这里，关于统计基础：3.1_假设检验综述的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
