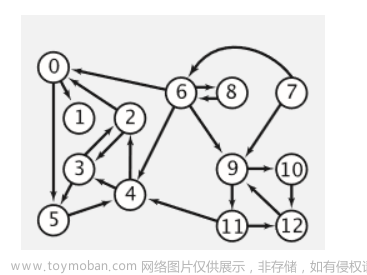
有向无环图:无环的有向图,简称DAG图(Directed Acycline Graph)

有向无环图常用来描述一个工程或系统的进行过程。(通常吧计划、施工、生产、程序流程等当成是一个工程)
一个工程可以分为若干个 子工程,只要完成了这些子工程(活动),就可以导致整个工程的完成
AOV网:拓扑排序
- 用一个有向图表示一个工程的各子工程及其相互制约的关系,其中以顶点表示活动,弧表示活动之间的优先制约关系,称这种有向图为顶点表示活动的网,简称AOV网(Activity On Vertex network)
拓扑排序:
在AOV网没有回路的前提下,我们将全部活动排序列成一个线性序列,使得若AOV网中有弧<i, j>存在,则在这个序列中,i一定排在j的前面,具有这种性质的线性序列称为拓扑有序序列,相应的拓扑有序排序算法称为拓扑排序。
例:排课表

|

|
拓扑排序的方法:
- 在有向图中选一个没有前驱的顶点输出
- 从图中删除该顶点和所有以它为尾的弧
- 重复上述两步,直到全部顶点均已输出;或者当图中不存在无前驱的顶点为止
例如排课表的拓扑排序:
C1,C2,C3,C4,C5,C7,C9,C10,C11,C6,C12,C8
C9,C10,C11,C6,C1,C12,C4,C2,C3,C5,C7,C8
一个AOV网的拓扑排序序列不是唯一的文章来源:https://www.toymoban.com/news/detail-502520.html
检测AOV网中是否存在环的方法:
对有向图构造其顶点的拓扑有序序列,若网中所有顶点都在它的突破普有序序列中,则该AOV网中必定不存在环文章来源地址https://www.toymoban.com/news/detail-502520.html
到了这里,关于有向无环图——AOV网(拓扑排序)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!