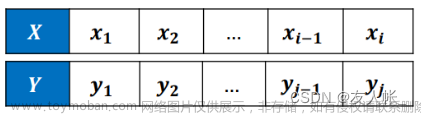
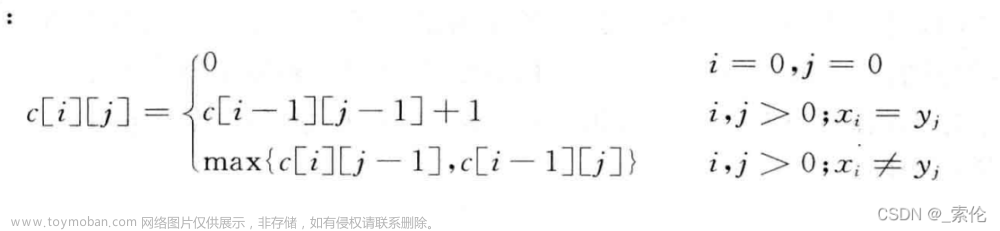算法-动态规划-最长有效括号-Toy模板网

这篇具有很好参考价值的文章主要介绍了算法-动态规划-最长有效括号。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

32. 最长有效括号

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例：

输入：s = "(()"
输出：2
解释：最长有效括号子串是 "()"

输入：s = ")()())"
输出：4
解释：最长有效括号子串是 "()()"

输入：s = ""
输出：0

思路分析

注意有效括号通常有两种形式：

重叠形式：（（...xx...））

并行形式：（...xx....）（...xx....）

dp[i]表示跟第i个字符组成的有效子串长度

dp[0]组不成有效串，为0

1，若"(" dp[i]=0 截止当前字符，无法组成有效子串,

2，若")" 分情况查看前面字符：

2.1，若前面字符是"("：

dp[i-2]+2

dp[i-2]前i-2个串的有效子串长度：dp[i-2]加上当前有效的"()"

2.2，若前面字符是")" ：

可能组成 "((xxx))" 则判断s[i-1-dp[i-1]]的字符是不是预期中的"("，若是的话则当前 dp[i-1]+2 。注意，也可能是这样的："（xxx)((xxx))"，还要加上可能存在的红色部分。

dp[i]=dp[i-2-dp[i-1]]+dp[i-1]+2

注意！边界情况的判断！文章来源地址https://www.toymoban.com/news/detail-502544.html

代码

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        n=len(s)
        if n<=1:
            return 0
        dp=[0]*n
        for i in range(1,n):
            if s[i]=="(":
                dp[i]=0
            else:
                #a==")"
                if s[i-1]=="(":
                    dp[i]=dp[i-2]+2 if i>=2 else 2
                if s[i-1]==")":
                    print("i=%s"%(i))
                    dp[i]=dp[i-2-dp[i-1]]+dp[i-1]+2 if i-1-dp[i-1]>=0 and s[i-1-dp[i-1]]=="(" else 0
                    #dp[i-2-dp[i-1]]+dp[i-1]+2 类似于（s1）（（s2）） s2长度+s1长度
                
            print("dp[%i]=%s"%(i,dp[i]))
        return max(dp)

到了这里，关于算法-动态规划-最长有效括号的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！