🚩 WRITE IN FRONT 🚩
- 🔎 介绍:"謓泽"正在路上朝着"攻城狮"方向"前进四" 🔎
- 🏅 荣誉:2021|2022年度博客之星物联网与嵌入式开发TOP5|TOP4、2021|2022博客之星TOP100|TOP63、阿里云专家博主、掘金优秀创作者、全网粉丝量6w+、全网访问量100w+ 🏅
- 🆔 文章内容由 謓泽 原创 如需相关转载请提前告知博主 ⚠
- 📝 个人主页:謓泽的博客 📃
- 📣 专栏系列:数据结构_謓泽的博客 📃
- 🎁 点赞👍+ 收藏⭐️+ 留言📝
- 📅 创作时间👉 挺久之前了,不记得了😶🌫️
- ✉️ 我们并非登上我们所选择的舞台,演出并非我们所选择的剧本 📩
🍭目录
💕 学习的重点
✨ who 时间「复杂度」
✨ 时间复杂度
🎉 大O的渐进表示法
🎉 推导大O阶的方法
💕 最优时间复杂度
💕 有些算法的时间不同情况
🧑💻 冒泡排序算法
💕 学习的重点
概述⇢在讲解数据结构之前、我们先来介绍下关于数据结构学习当中的重点目标知识点。
说明⇢数据结构的学习方面分为两个方面。
⒈各种数据结构的定义、特性、适用场景。掌握这些理论基础,你才能知道什么场景下应该
使用链表、红黑树、哈希表。
⒉其次能够使用一种语言熟练的实现这些数据结构。一般在项目开发当中,我们是不需要自己实现数据结构的、一般成熟的面向对象都有自己的数据结构库、如C++的STL(C++算法当中的库),Java的集合类。但是造轮子是一个深度的学习过程,经过这样的学习,你对数据结构的理解就脱胎换骨了,能够更加高效的使用他们。其次技术进阶的一个必经之路就是学习开源的项目,很多的开源项目都用了很多的数据结构,数据结构不扎实的话就相当于技术进阶的拦路虎。
✨ who 时间「复杂度」
说明⇢算法效率分析分为两种。
⒈时间效率。
解释⇢时间效率被称之为是时间复杂度。时间复杂度主要衡量的是一个算法的运行速度。在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费多的时间,从理论来说,是不能算出来的,只有你把你的程序仿真机器跑起来的话,才能够被知道。但是我们需要每个算法都要进行上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度的这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
⒉空间效率。
解释⇢空间效率被称之为是空间复杂度。空间复杂度主要是衡量的是一个算法所需要的额外的空间,在计算机发展的早期时代,计算机的存储容量已经到达了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
⒊注意。
说明⇢实际当中我们最最关心得还是时间效率。
✨ 时间复杂度
✔重点再次强调下⇢算法中的基本操作的执行次数,为算法的时间复杂度。
🍊示例代码如下⇲
#define _CRT_SECURE_NO_WARNINGS 1 #include<stdio.h> void fun(N) { int i = 0; int j = 0; int count = 0;//计算被执行多少次。 for (i = 0; i < N; i++) { for (j = 0; j < N; j++) { count++; } } printf("count1=%d\n", count); for (i = 0; i < 2 * N; i++) { count++; } printf("count2=%d\n", count-100); i = 10; while (i--) { count++; } printf("count3=%d\n", count-120); } int main(void) { #define N 10 fun(N); }运行结果🖋
count1=100
count2=20
count3=10
📝说明⇢这里我们需要知道的是fun所执行的次数。
表达式-F(N) = N²+2*N+N
- N = 10 F(N) = 130 ⇿ O(N²)
- N = 100 F(N) = 10210 ⇿ O(2*N)
- N = 1000 F(N) = 1002010 ⇿ O(N)
📝说明⇢随着N的表达式越大、N²对结果的影响是最大的,在上述中分别是100、10000、1000000的。
😶🌫️注意⇢在上述的例题是只有一个未知数的,而时间复杂度不仅仅只有一个未知数,有些题目有两个甚至多个。
🎉 大O的渐进表示法
📝说明⇢这个大O的渐进表示法实际上就是一个估算。那么在上述的示例代码就会写成时间复杂度:O(N²) 在表达式当中不会去看后面的两项,因为对结果影响不大。类似于数学当中的极限。
🉑解释大O符号(Big O notation)⇢用于描述函数渐进的行为数字符号。
🎓总结⇢时间复杂度它是一个估算,是去看表达式当中影响值最大的那一项、也可以说是保留最高阶项。
🎉 推导大O阶的方法
⒈用常数1取代运行时间中的所有加法常数,即使这个常数再大,算法的时间复杂度还是O(1)
⒉修改后的运行次数函数当中,只保留最高阶项。
⒊如果最高阶项存在且不是1(常数),则去除与这个项目相乘的常数。得到结果就是大O阶。注意⇢同等数量级可忽略!
- 以上三点请牢牢记住!
- 注:N相当于是算法当中执行次数。
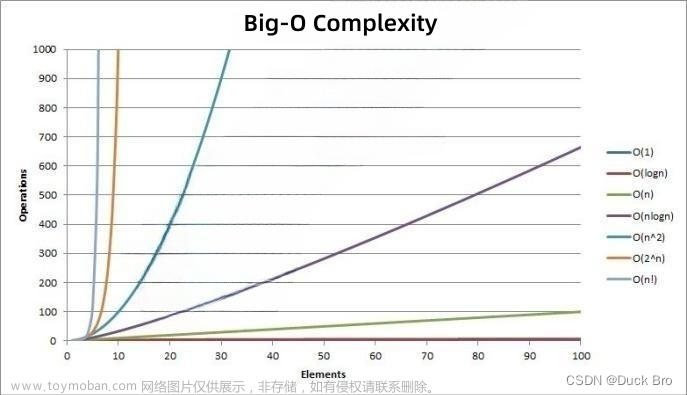
💕 最优时间复杂度
第一个肯定是O(1)随着数量次数的增加,次数是不会改变的。如果一个算法是O(1)的话、那么它就是最🐂的,不可能有比O(1)更牛的算法了。
第二个其次就是O(logN)、像二分查找有序的它的时间复杂度就是O(logN)
说明⇢1*2*2*2...*2=N、2^X=N、X=log₂(底数)N(真数)。
loga(底数)b(真数)=X ⇿ a^x=b 「对数函数」
举个例子吧,假设N=1000 那么logN=(1000=2^10) 这里就相当于你如果没有用二分查找那么你的时间复杂度相当于是O(N)、你用了二分查找法只是O(logN)
说明⇢这里如果N=1000、那么logN=10 从这里就可以看出O(logN)和O(1)是一个量级的。
注意⇢算法的复杂度计算,喜欢简写成为logN,因为很多地方不好写底数。
第三个是O(N)算是普遍来说最普通的时间复杂度了,也是我们实际情况遇到最多的。
第四个是O(N^2)这个就比较花费执行次数了。
第五个效率最低的就是O(N!)了。
💕 有些算法的时间不同情况
- 最好的情况-任意输入规模的最小运行次数O(1)。(下界)
- 平均的情况-任意输入规模的期望运行次数O(N/2)。
- 最坏的情况-任意输入规模的最大运行次数O(N)。(上界)
- 最好的情况-1次找到。
- 最坏的情况-N次找到。
- 平均的情况-N/2次找到。
📝说明⇢在实际的情况当中一般我们关注算法是最坏的运行情况,所以数组中搜索数据时间复杂度为O(N)
🧑💻 冒泡排序算法
📝说明⇢相信看过前面C语言部分的小伙伴,应该知道什么是冒泡排序,那么我们就来求下冒泡排序当中的时间复杂度是多少。
#pragma warning(disable:6031) #pragma message("第xxx题→冒泡排序") #define _CRT_SECURE_NO_WARNINGS 1 #include<stdio.h> void sort_jx(int arr1[],int sz) { int i = 0; //1.确定总的排序次数 //2.相邻之间的元素比较 //3.确定比较次数,然后进行交换。 for (i = 0; i < sz; i++) { int j = 0; for (j = 0; j < sz-1-i; j++) { if (arr1[j] < arr1[j + 1]) { int temp = 0; temp = arr1[j]; arr1[j] = arr1[j + 1]; arr1[j + 1] = temp; } } } } void sort_sx(int arr2[],int sz) { int i = 0; //1.确定总的排序次数 //2.相邻之间的元素比较 //3.确定比较次数,然后进行交换。 for (i = 0; i < sz; i++) { int j = 0; for (j = 0; j < sz - 1 - i; j++) { if (arr2[j] > arr2[j + 1]) { int temp = 0; temp = arr2[j]; arr2[j] = arr2[j + 1]; arr2[j + 1] = temp; } } } } void traversal(int arr1[], int arr2[], int sz) { int i = 0; for (i = 0; i < sz; i++) { printf("%d ", arr1[i]); } printf("\n"); for (i = 0; i < sz; i++) { printf("%d ", arr2[i]); } } int main(void) { int i = 0; int arr1[] = { 2,1,3,4,5,6,7,8,9,10 }; int arr2[] = { 10,9,8,7,6,5,4,3,2,1 }; int sz = sizeof(arr1) / sizeof(arr2[0]); sort_jx(arr1,sz); sort_sx(arr2,sz); traversal(arr1,arr2,sz); return 0; }第一趟冒泡:N
第二趟冒泡:N-1
第三趟冒泡:N-2
第N 趟冒泡:1
拓展知识点⇢在这里我们可以用等差数列的公式来计算-(首项+尾项)*项数/2⇿(N+1)*N/2
说明⇢时间复杂度:O(N²)
注意⇢不是说一层循环就是:O(N²)、两层循环就是:O(N²)、具体情况要根据题目去分析。文章来源:https://www.toymoban.com/news/detail-502698.html
文章来源地址https://www.toymoban.com/news/detail-502698.html
到了这里,关于【数据结构】时间复杂度的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!